Понятие двоичных циклических кодов

1.2. Понятие двоичных циклических кодов.

 

1.2.1. Общие понятия и определения.

 

Любой групповой (n, k) – код может быть записан в виде матрицы, включающей  k линейно-независящих строк по n символов, и, наоборот, любая совокупность k линейно-независящих n-разрядных кодовых комбинаций может рассматриваться как образующая матрица некоторого группового кода. Среди всего многообразия таких кодов можно выделить коды, у которых строки образующих матриц связаны дополнительным условием цикличности.

Все строки образующей матрицы такого кода могут быть получены циклическим сдвигом одной комбинации, называемой образующей для данного кода. Коды, удовлетворяющие этому условию, получили название циклических.

Циклические коды относятся к числу блоковых систематических кодов, в которых каждая комбинация кодируется самостоятельно (в виде блока) таким образом, что информационные k и контрольные m символы всегда находятся на определенных местах.

Возможность обнаружения и исправления практически любых ошибок при относительно малой избыточности по сравнению с другими кодами, а также простота схемной реализации аппаратуры кодирования и декодирования сделали эти коды широко распространенными.

Теория циклических кодов базируется на теории групп и алгебре многочленов над полем Галуа.

Многочлен (полином), который можно представить в виде произведения многочленов низших степеней, называют приводимым (в данном поле), в противном случае не приводимым. Неприводимые многочлены играют роль, сходную с простыми числами в теории чисел. Неприводимые многочлены P(X) можно записать в виде десятичных или двоичных чисел, либо в виде алгебраического многочлена.

Многочлен в поле двоичных чисел называется неприводимым, если он делится без остатка только на себя или на единицу.

В основу циклического кодирования положено использование неприводимого многочлена P(X), который применительно к циклическим кодам называется образующим, генератором или производящим многочленом (полиномом) .

1.2.2. Методы построения циклических кодов.

В качестве информационных символов k для построения циклических кодов берут комбинацию двоичного кода на все сочетания. В общем случае, если заданную кодовую комбинацию G(X) умножить на образующий многочлен P(X) , получится циклический код, обладающий теми или иными корректирующими свойствами в зависимости от выбора P(X). Однако в этом коде контрольные символы m будут располагаться в самых разнообразных местах кодовой комбинации. Такой код не является систематическим, что затрудняет его схемную реализацию. Ситуацию можно значительно упростить, если контрольные символы приписать в конце кода, т. е. после информационных символов.

Для этой цели удобно воспользоваться следующим методом.

1.   Умножаем кодовую комбинацию G(X), которую мы хотим закодировать, на одночлен X^m , имеющий ту же степень, что и образующий многочлен P(X).

2.   Делим произведение G(X)X^m  на образующий многочлен P(X).

 

G(X)X^m / P(x)=Q(X)+R(X)/P(X), (1.1)

 

где Q(X) - частное от деления; R(X) – остаток.

Умножая выражение (1) на P(X) и перенося R(X) в другую часть равенства, согласно правилам алгебры двоичного поля, т. е. без перемены знака на обратный, получаем

 

F(X)=G(X)P(x)= G(X)X^m+R(X). (1.2)

 

Таким образом, согласно (2) , циклический код, т.е. закодированное сообщение F(X), можно образовать двумя способами:

1)   умножением одной из комбинаций двоичного кода на все сочетания [комбинация Q)(X) к той же группе того же кода, что и заданная комбинация G(X)] на образующий многочлен P(X).

2)   умножением заданной кодовой комбинации G(X) на одночлен X^m, имеющий ту же степень, что и образующий многочлен P(X), с добавлением к этому произведению остатка R(X), полученного после деления произведения G(X)X^m на образующий многочлен P(X).

Свойства образующего многочлена:

1.   Все разрешенные комбинации циклического кода делятся на образующий многочлен без остака.

2.   На образующий многочлен делится без остатка двучлен Xⁿ+1.

1.3. Технические средства кодирования для двоичных циклических кодов.

Основу кодирующих и декодирующих устройств двоичных циклических кодов составляют регистры сдвига с обратными связями, позволяющие осуществлять как умножение, так и деление многочленов с приведением коэффициентов по модулю 2.

Все известные кодирующие устройства для любых типов циклических кодов, выполненные на регистрах сдвига, можно к двум типам схем согласно методам кодирования рассмотренным выше.

С помощью схем первого типа вычисляются значения проверочных символов путем непосредственного деления многочлена G(X)X^m на образующий многочлен P(X). Это делается с помощью регистра сдвига, содержащего n-k разрядов (рис.1.1). В этой схеме коэффициенты кодируемого многочлена участвуют в обратной связи не через n-k сдвигов, а сразу с первого такта. Это позволяет устранить разрыв между информационными и проверочными символами.

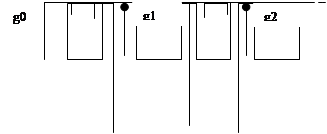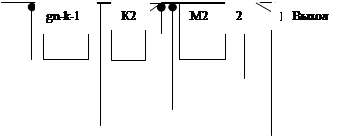Рис. 1.1. Кодирующее устройство для циклического кода на основе (n-k) – разрядного регистра сдвига.

В исходном состоянии ключ К1 находится в положении 1, а ключ К2 замкнут. Информационные символы одновременно поступают как в линию связи, так и в регистр сдвига, где за k тактов образуется остаток. Затем ключ К2 размыкается, ключ К1 переходит в положение 2 и остаток поступает в линию связи.

С помощью схем второго типа вычисляют значения проверочных символов как линейную комбинацию информационных символов, т. е. построены на основе систематических кодов. Кодирующее устройство строится на основе k-разрядного регистра сдвига. Выходы ячеек памяти подключаются к сумматору в цепи обратной связи в соответствии с видом генераторного многочлена