Навигация
Соединение оптических волокон
2.1.1. Соединение оптических волокон
Развитие волоконно-оптических телекоммуникационных технологий в основном определяется качеством волоконно-оптических кабелей (ВОК) на многомодовых и одномодовых оптических волокнах, изготовленных методом покрытия кварцевой жилы полимерными или кварцевыми материалами. Некоторые из этих волокон в настоящее время по ряду характеристик приблизились к предельно возможным показателям. Так, одномодовое волокно с рабочей длиной волны 1,55 мкм практически достигло предела по затуханию, равного 0,154 дБ/км. Это позволило в настоящее время строить регенерационные участки длиной до 200 км и более, снижая тем самым затраты на строительство волоконно-оптических линий связи. Однако ввиду естественных ограничений производить волокна таких длин не представляется возможным. Поэтому осуществляют соединение оптических волокон, называя участок между соединениями строительной длиной. Снижение коэффициента затухания оптического волокна обуславливает ужесточение требований к качеству соединений. Это объясняется тем, что число таких соединений, как правило, достаточно велико. Иные требования предъявляются к устройствам соединения волоконно-оптических кабелей, предназначенных для локальных сетей, имеющих небольшие длины участков. Данные устройства должны быть компактными, допускать многоразовое соединение и отличаться простотой выполнения соединения [5].
2.2. Оптическое волокно. Общие положенияВажнейший из компонентов ВОЛС - оптическое волокно. Для передачи сигналов применяются два вида волокна: одномодовое и многомодовое. Свое название волокна получили от способа распространения в них излучения.
Оптическое волокно (рис. 2.1) состоит из сердцевины, по которой происходит распространение световых волн, и оболочки, предназначенной, с одной стороны, для создания лучших условий отражения на границе раздела «сердцевина - оболочка», а с другой - для снижения излучения энергии в окружающее пространство. С целью повышения прочности и тем самым надежности волокна поверх оболочки, как правило, накладываются защитные упрочняющие покрытия.
Рис 2.1. Общий вид типового ОВ.
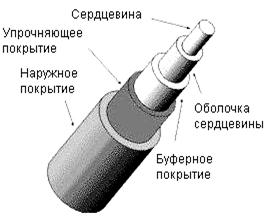
Такая конструкция ОВ используется в большинстве оптических кабелей (ОК) в качестве базовой [5]. Сердцевина изготавливается из оптически более плотного материала. Оптические волокна отличаются диаметром сердцевины и оболочки, а также профилем показателя преломления сердцевины, т.е. зависимостью показателя преломления от расстояния от оси ОВ (см. рис 2.3).
Все оптические волокна делятся на две основные группы: многомодовые MMF (multi mode fiber) и одномодовые SMF (single mode fiber). В многомодовых ОВ, имеющих диаметр светонесущей жилы на порядок больше длины волны передачи, распространяется множество различных типов световых лучей - мод. Многомодовые волокна разделяются по профилю показателя преломления на ступенчатые (step index multi mode fiber) и градиентные (graded index multi mode fiber).
2.3. Распространение световых лучей в оптических волокнахОсновными факторами, влияющими на характер распространения света в волокне, наряду с длиной волны излучения, являются: геометрические параметры волокна, затухание, дисперсия.
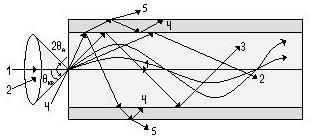 |
Рис. 2.2. Распространение излучения по ступенчатому и градиентному многомодовым и одномодовому ОВ.
Принцип распространения оптического излучения вдоль оптического волокна основан на явлении полного внутреннего отражения на границе сред с разными показателями преломления. Процесс распространения световых лучей в оптически более плотной среде, окруженной менее плотной показан на рис. 2.2. Угол полного внутреннего отражения, при котором падающее на границу оптически более плотной и оптически менее плотной сред излучение полностью отражается, определяется соотношением:
![]() , (2.3.1)
, (2.3.1)
где n1 - показатель преломления сердцевины ОВ, n2 - показатель преломления оболочки ОВ, причем n1 > n2. При попадании светового излучения на торец ОВ в нем могут распространяться три типа световых лучей, называемые направляемыми, вытекающими и излучаемыми лучами, наличие и преобладание какого-либо типа лучей определяется углом их падения на границу раздела «сердцевина - оболочка». Те лучи, которые падают на границу раздела под углом ![]() (лучи 1, 2 и 3), отражаются от нее и вновь возвращаются в сердцевину волокна, распространяясь в ней и не претерпевая преломления. Так как траектории таких лучей полностью расположены внутри среды распространения — сердцевины волокна, они распространяются на большие расстояния и называются направляемыми.
(лучи 1, 2 и 3), отражаются от нее и вновь возвращаются в сердцевину волокна, распространяясь в ней и не претерпевая преломления. Так как траектории таких лучей полностью расположены внутри среды распространения — сердцевины волокна, они распространяются на большие расстояния и называются направляемыми.
Лучи, падающие на границу раздела под углами ![]() (лучи 4), носят название вытекающих лучей (лучей оболочки). Достигая границы «сердцевина - оболочка», эти лучи отражаются и преломляются, теряя каждый раз в оболочке волокна часть энергии, в связи с чем исчезают вовсе на некотором расстоянии от торца волокна. Лучи, которые излучаются из оболочки в окружающее пространство (лучи 5), носят название излучаемых лучей и возникают в местах нерегулярностей или из-за скручивания ОВ. Излучаемые и вытекающие лучи являются паразитными и приводят к рассеиванию энергии и искажению информационного сигнала.
(лучи 4), носят название вытекающих лучей (лучей оболочки). Достигая границы «сердцевина - оболочка», эти лучи отражаются и преломляются, теряя каждый раз в оболочке волокна часть энергии, в связи с чем исчезают вовсе на некотором расстоянии от торца волокна. Лучи, которые излучаются из оболочки в окружающее пространство (лучи 5), носят название излучаемых лучей и возникают в местах нерегулярностей или из-за скручивания ОВ. Излучаемые и вытекающие лучи являются паразитными и приводят к рассеиванию энергии и искажению информационного сигнала.
В общем случае распространение электромагнитных волн описывается системой уравнений Максвелла в дифференциальной форме:
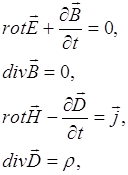 (2.4.1)
(2.4.1)
где ![]() - плотность электрического заряда,
- плотность электрического заряда, ![]() и
и ![]() – напряженности электрического и магнитного полей соответственно,
– напряженности электрического и магнитного полей соответственно, ![]() – плотность тока,
– плотность тока, ![]() и
и ![]() – электрическая и магнитная индукции.
– электрическая и магнитная индукции.
Если представить напряженность электрического и магнитного поля ![]() и
и ![]() при помощи преобразования Фурье [5]:
при помощи преобразования Фурье [5]:
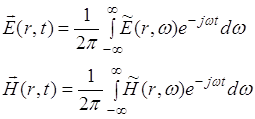 , (2.4.2)
, (2.4.2)
то волновые уравнения примут вид:
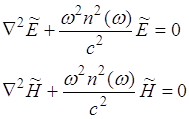 , (2.4.3)
, (2.4.3)
где ![]() - оператор Лапласа.
- оператор Лапласа.
Световод можно представить идеальным цилиндром с продольной осью z, оси х и у в поперечной (ху) плоскости образуют горизонтальную (xz) и вертикальную (xz) плоскости. В этой системе существуют 4 класса волн (Е и Н ортогональны):
поперечные Т: Ez = Нz = 0; Е = Еy; Н = Нx;
электрические Е: Еz = 0, Нz = 0; Е = (Еy , Еz) - распространяются в плоскости (yz); Н = Нx ;
магнитные Н: Нz = 0, Еz = 0; Н = (Нx , Нz) - распространяются в плоскости (xz), E = Ez;
смешанные ЕН или НЕ: Еz = 0, Нz = 0; Е = (Еy , Еz), Н = (Нx , Нz) - распространяются в плоскостях (xz) и (yz).
При решении системы уравнений Максвелла удобнее использовать цилиндрические координаты (z, r, φ), при этом решение ищется в виде волн с компонентами Ez , Нz вида:
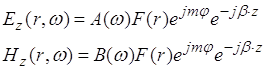 , (2.4.4)
, (2.4.4)
где ![]() и
и ![]() - нормирующие постоянные,
- нормирующие постоянные, ![]() - искомая функция,
- искомая функция, ![]() - продольный коэффициент распространения волны.
- продольный коэффициент распространения волны.
Решения для ![]() получаются в виде наборов из m (появляются целые индексы m) простых функций Бесселя
получаются в виде наборов из m (появляются целые индексы m) простых функций Бесселя ![]() для сердцевины и модифицированных функций Ханкеля
для сердцевины и модифицированных функций Ханкеля ![]() для оболочки, где
для оболочки, где ![]() и
и ![]() - поперечные коэффициенты распространения в сердцевине и оболочке соответственно,
- поперечные коэффициенты распространения в сердцевине и оболочке соответственно, ![]() - волновое число. Параметр
- волновое число. Параметр ![]() определяется как решение характеристического уравнения, получаемого из граничных условий, требующих непрерывности тангенциальных составляющих компонент Ez и Нz электромагнитного поля на границе раздела сердцевины и оболочки. Характеристическое уравнение, в свою очередь, дает набор из n решений (появляются целые индексы n) для каждого целого m, т.е. имеем
определяется как решение характеристического уравнения, получаемого из граничных условий, требующих непрерывности тангенциальных составляющих компонент Ez и Нz электромагнитного поля на границе раздела сердцевины и оболочки. Характеристическое уравнение, в свою очередь, дает набор из n решений (появляются целые индексы n) для каждого целого m, т.е. имеем ![]() собственных значений, каждому из которых соответствует определенный тип волны, называемый модой. В результате формируется набор мод, перебор которых основан на использовании двойных индексов.
собственных значений, каждому из которых соответствует определенный тип волны, называемый модой. В результате формируется набор мод, перебор которых основан на использовании двойных индексов.
Условием существования направляемой моды является экспоненциальное убывание ее поля в оболочке вдоль координаты r , что определяется значением поперечного коэффициента распространения в оболочке. При ![]() = 0 устанавливается критический режим, заключающийся в невозможности существования направляемой моды, что соответствует [5]:
= 0 устанавливается критический режим, заключающийся в невозможности существования направляемой моды, что соответствует [5]:
![]() . (2.4.5)
. (2.4.5)
Последнее уравнение имеет бесчисленное множество решений [5]:
![]()
(2.4.6)
Введем величину, называемую нормированной частотой V, которая связывает структурные параметры ОВ и длину световой волны, и определяемую следующим выражением:
![]() , (2.4.7)
, (2.4.7)
При ![]() = 0 для каждого из решений уравнения (2.4.5) имеет место критическое значение нормированной частоты
= 0 для каждого из решений уравнения (2.4.5) имеет место критическое значение нормированной частоты ![]() (m = 1, 2, 3…, n = 0, 1, 2, 3…):
(m = 1, 2, 3…, n = 0, 1, 2, 3…):
![]()
![]() и т.д.
и т.д.
Для моды HE11 критическое значение нормированной частоты ![]() . Эта мода распространяется при любой частоте и структурных параметрах волокна и является фундаментальной модой ступенчатого ОВ. Выбирая параметры ОВ можно добиться режима распространения только этой моды, что осуществляется при условии:
. Эта мода распространяется при любой частоте и структурных параметрах волокна и является фундаментальной модой ступенчатого ОВ. Выбирая параметры ОВ можно добиться режима распространения только этой моды, что осуществляется при условии:
![]() (2.4.8)
(2.4.8)
Минимальная длина волны, при которой в ОВ распространяется фундаментальная мода, называется волоконной длиной волны отсечки. Значение определяется из последнего выражения как:
![]() (2.4.9)
(2.4.9)
Одномодовые волокна подразделяются на ступенчатые одномодовые волокна (step index single mode fiber) или стандартные волокна SF (standard fiber), на волокна со смещенной дисперсией DSF (dispersion-shifted single mode fiber), и на волокна с ненулевой смещенной дисперсией NZDSF (non-zero dispersion-shifted single mode fiber).
В ступенчатом одномодовом оптическом волокне (SF) (рис. 2.3) диаметр светонесущей жилы составляет 8-10 мкм и сравним с длиной световой волны. В таком волокне при достаточно большой длине волны света λ > λCF (λCF - длина волны отсечки) распространяется только один луч (одна мода). Одномодовый режим в оптическом волокне реализуется в окнах прозрачности 1310 нм и 1550 нм. Распространение только одной моды устраняет межмодовую дисперсию и обеспечивает очень высокую пропускную способность одномодового волокна в этих окнах прозрачности. Наилучший режим распространения с точки зрения дисперсии достигается в окрестности длины волны 1310 нм, когда хроматическая дисперсия обращается в ноль. С точки зрения потерь это не самое лучшее окно прозрачности. В этом окне потери составляют 0,3 - 0,4 дБ/км, в то время как наименьшее затухание 0,20 - 0,25 дБ/км достигается в окне 1550 нм.
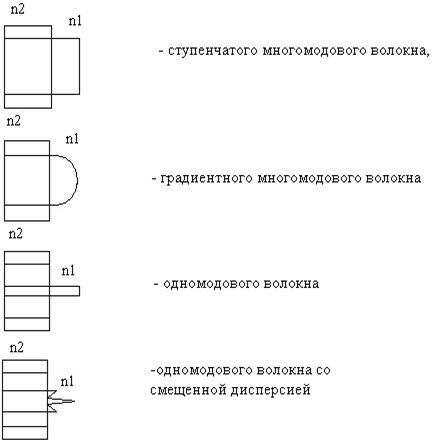 |
Рис. 2.3. Профили показателя преломления
В одномодовом оптическом волокне со смещенной дисперсией (DSF) (рис. 2.3) длина волны, на которой дисперсия обращается в ноль, - длина волны нулевой дисперсии λ0 - смещена в окно прозрачности 1550 нм. Такое смещение достигается благодаря специальному профилю показателя преломления волокна. Таким образом, в волокне со смещенной дисперсией реализуются наилучшие характеристики, как по минимуму дисперсии, так и по минимуму потерь. Поэтому такое волокно лучше подходит для строительства протяженных сегментов с расстоянием между ретрансляторами до 100 и более км. Разумеется, единственная рабочая длина волны берется близкой к: 1550 нм.
Одномодовое оптическое волокно с ненулевой смещенной дисперсией NZDSF в отличие от DSF оптимизировано для передачи не одной длины волны, а сразу нескольких длин волн (мультиплексного волнового сигнала) и наиболее эффективно может использоваться при построении магистралей «полностью оптических сетей» - сетей, на узлах которых не происходит оптоэлектронного преобразования при распространении оптического сигнала.
Оптимизация трех перечисленных типов одномодовых ОВ совершенно не означает, что они всегда должны использоваться исключительно под определенные задачи: SF - передача сигнала на длине волны 1310 нм, DSF - передача сигнала на длине волны 1550 нм, NZDSF - передача мультиплексного сигнала в окне 1530-1560 нм. Так, например, мультиплексный сигнал в окне 1530-1560 нм можно передавать и по стандартному ступенчатому одномодовому волокну SF [5]. Однако длина безретрансляционного участка при использовании волокна SF будет меньше, чем при использовании NZDSF, или иначе потребуется очень узкая полоса спектрального излучения лазерных передатчиков для уменьшения результирующей хроматической дисперсии. Максимальное допустимое расстояние определяется техническими характеристиками как самого волокна (затуханием, дисперсией), так и приемопередающего оборудования (мощностью, частотой, спектральным уширением излучения передатчика, чувствительностью приемника).
В ВОЛС наиболее широко используются следующие стандарты волокон:
- многомодовое градиентное волокно 50/125;
- многомодовое градиентное волокно 62,5/125;
- одномодовое ступенчатое волокно SF (волокно с несмещенной дисперсией или стандартное волокно) 8-10/125;
- одномодовое волокно со смещенной дисперсией DSF 8-10/125;
- одномодовое волокно с ненулевой смещенной дисперсией NZDSF (по профилю показателя преломления это волокно схоже с предыдущим типом волокна).
2.6. Константа распространения и фазовая скоростьВолновое число k можно рассматривать как вектор, направление которого совпадает с направлением распространения света в объемных средах. Этот вектор называется волновым вектором. В среде с показателем преломления ![]() величина волнового вектора равна
величина волнового вектора равна ![]() . В случае распространения света внутри волновода направление распространения света совпадает с направлением проекции β волнового вектора k, на ось волновода:
. В случае распространения света внутри волновода направление распространения света совпадает с направлением проекции β волнового вектора k, на ось волновода:
![]() (2.6.1)
(2.6.1)
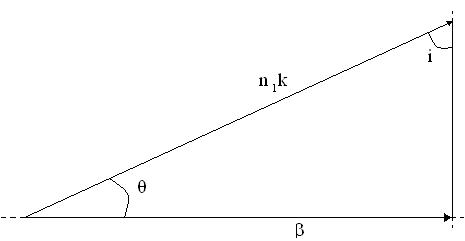 |
где
Рис. 2.4. Волновой вектор и константа распространения
Угол падения ![]() изменяется между
изменяется между ![]() и π/2. Следовательно:
и π/2. Следовательно:
![]() (2.6.2)
(2.6.2)
Таким образом, величина константы распространения внутри волновода всегда лежит между значениями волновых чисел плоской световой волны в материале сердцевины и оболочки. Если учесть, что 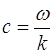 , то можно переписать это соотношение на языке фазовых скоростей:
, то можно переписать это соотношение на языке фазовых скоростей:
![]() (2.6.3)
(2.6.3)
Фазовые скорости распространения мод 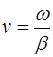 заключены между фазовыми скоростями волн в двух объемных материалах.
заключены между фазовыми скоростями волн в двух объемных материалах.
Скорость распространения светового сигнала или групповая скорость - это скорость распространения огибающей светового импульса. В общем случае групповая скорость u не равна фазовой скорости. Различие фазовых скоростей мод приводит к искажению входного пучка света по мере его распространения в волокне.
В волокне с параболическим градиентным показателем преломления наклонные лучи распространяются по криволинейной траектории, которая, естественно, длиннее, чем путь распространения аксиального луча. Однако из-за уменьшения показателя преломления по мере удаления от оси волокна, скорость распространения составляющих светового сигнала при приближении к оболочке оптического волокна возрастает, так что в результате этого время распространения составляющих по ОВ оказывается примерно одинаковым. Таким образом, дисперсия или изменение времени распространения различных мод, сводится к минимуму, а ширина полосы пропускания волокна увеличивается. Точный расчет показывает, что разброс групповых скоростей различных мод в таком волокне существенно меньше, чем в волокне со ступенчатым профилем показателя преломления. Оптические волокна, которые могут поддерживать распространение только моды самого низкого порядка, называются одномодовыми.
Таким образом, каждая мода, распространяющаяся в ОВ, характеризуется постоянным по длине световода распределением интенсивности в поперечном сечении, постоянной распространения β, а также фазовой v и групповой u скоростями распространения вдоль оптической оси, которые различны для разных мод. Из-за различия фазовых скоростей мод волновой фронт и распределение поля в поперечном сечении изменяются вдоль оси волокна. Из-за различия групповых скоростей мод световые импульсы расширяются, и это явление называется межмодовой дисперсией.
В одномодовом волокне существует только одна мода распространения, поэтому такое волокно характеризуется постоянным распределением поля в поперечном сечении, в нем отсутствует межмодовая дисперсия, и оно может передавать излучение с очень широкой полосой модуляции, ограниченной только другими видами дисперсии (см. п. 3.2).
Глава 3. Процессы, происходящие в оптическом волокне, и их влияние на скорость и дальность передачи информации 3.1. Затухание оптического волокна
По мере распространения света в оптической среде он ослабевает, что носит название затухания среды — затухания ОВ. Затухание зависит от длины волны излучения, вводимого в волокно. В настоящее время передача сигналов по волокну осуществляется в трех диапазонах: 850 нм, 1300 нм, 1550 нм, так как именно в этих диапазонах кварц имеет повышенную прозрачность. Затухание (рис. 3.1) обычно измеряется в дБ/км и определяется потерями на поглощение и на рассеяние излучения в оптическом волокне [5]:
- рэлеевское рассеяние;
- рассеяние на дефектах волокна;
- собственное поглощение кварцевого стекла;
- примесное поглощение;
- поглощение на микро и макроизгибах.
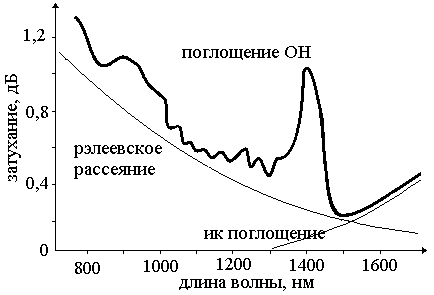 |
Рис. 3.1. Затухание.
Степень потерь определяется коэффициентом затухания ![]() , который в общем виде равен:
, который в общем виде равен:
![]() (3.1.1)
(3.1.1)
где ![]() — коэффициент затухания, обусловленный потерями на поглощение световой энергии. Собственное поглощение кварцевого стекла определяется поглощением фотонов при котором энергия фотона переходит в энергию электронов или в колебательную энергию решетки. Спектр собственного электронного поглощения кварцевого стекла лежит в ультрафиолетовой области (
— коэффициент затухания, обусловленный потерями на поглощение световой энергии. Собственное поглощение кварцевого стекла определяется поглощением фотонов при котором энергия фотона переходит в энергию электронов или в колебательную энергию решетки. Спектр собственного электронного поглощения кварцевого стекла лежит в ультрафиолетовой области (![]() < 0,4 мкм). Спектр поглощения решетки лежит в инфракрасной области (
< 0,4 мкм). Спектр поглощения решетки лежит в инфракрасной области (![]() > 7 мкм). Поскольку структура кварцевого стекла аморфная, полосы поглощения имеют размытые границы, а их «хвосты» заходят в видимую область спектра. Во втором и третьем окнах прозрачности в ди8=]апазоне длин волн 1,3-1,6 мкм потери, вызванные собственным поглощением, имеют порядок 0,03 дБ/км.
> 7 мкм). Поскольку структура кварцевого стекла аморфная, полосы поглощения имеют размытые границы, а их «хвосты» заходят в видимую область спектра. Во втором и третьем окнах прозрачности в ди8=]апазоне длин волн 1,3-1,6 мкм потери, вызванные собственным поглощением, имеют порядок 0,03 дБ/км.
![]() — коэффициент затухания, обусловленный рэлеевским рассеиванием на неоднородностях материала ОВ, размеры которых значительно меньше длины световой волны, и тепловыми флуктуациями показателя преломления. Этот вид рассеяния определяет теоретическую границу, ниже которой затухание не может быть уменьшено и в современных ОВ является основным источником потерь в рабочих областях спектра. Рэлеевское рассеяние вызывается рассеянием на неоднородностях показателя преломления, возникших в расплавленном кварце в связи с локальными термодинамическими флуктуациями концентрации молекул (плотности) кварца из-за их хаотического движения в расплавленном состоянии. При затвердевании волокна неоднородности, возникшие в расплавленной фазе, застывают в структуре кварцевого стекла. Колебания плотности приводят к случайным флуктуациям показателя преломления в масштабе, меньшем, чем длина световой волны
— коэффициент затухания, обусловленный рэлеевским рассеиванием на неоднородностях материала ОВ, размеры которых значительно меньше длины световой волны, и тепловыми флуктуациями показателя преломления. Этот вид рассеяния определяет теоретическую границу, ниже которой затухание не может быть уменьшено и в современных ОВ является основным источником потерь в рабочих областях спектра. Рэлеевское рассеяние вызывается рассеянием на неоднородностях показателя преломления, возникших в расплавленном кварце в связи с локальными термодинамическими флуктуациями концентрации молекул (плотности) кварца из-за их хаотического движения в расплавленном состоянии. При затвердевании волокна неоднородности, возникшие в расплавленной фазе, застывают в структуре кварцевого стекла. Колебания плотности приводят к случайным флуктуациям показателя преломления в масштабе, меньшем, чем длина световой волны ![]() .
.
![]() — коэффициент затухания, вызванный присутствующими в ОВ примесями, приводящими к дополнительному поглощению оптической мощности, это ионы металлов (Fe, Cu, Ni, Mn, Cr), вызывающие поглощение в диапазоне длин волн 0,6-1,6 мкм, и гидроксильные группы (ОН), из-за которых появляются резонансные всплески затухания
— коэффициент затухания, вызванный присутствующими в ОВ примесями, приводящими к дополнительному поглощению оптической мощности, это ионы металлов (Fe, Cu, Ni, Mn, Cr), вызывающие поглощение в диапазоне длин волн 0,6-1,6 мкм, и гидроксильные группы (ОН), из-за которых появляются резонансные всплески затухания ![]() на длинах волн 0,75 мкм, 0, 97 мкм и 1,39 мкм.
на длинах волн 0,75 мкм, 0, 97 мкм и 1,39 мкм.
![]() — дополнительные потери, определяемые деформацией ОВ в процессе изготовления кабеля, вызванной скруткой, изгибом, отклонением от прямолинейного расположения и термомеханическими воздействиями, имеющими место при наложении оболочек и покрытий на сердцевину волокна при изготовлении ОК (их называют кабельными).
— дополнительные потери, определяемые деформацией ОВ в процессе изготовления кабеля, вызванной скруткой, изгибом, отклонением от прямолинейного расположения и термомеханическими воздействиями, имеющими место при наложении оболочек и покрытий на сердцевину волокна при изготовлении ОК (их называют кабельными).
![]() — коэффициент затухания, зависящий от длины волны оптического излучения и за счет поглощения в инфракрасной области возрастающий в показательной степени с ростом длины волны.
— коэффициент затухания, зависящий от длины волны оптического излучения и за счет поглощения в инфракрасной области возрастающий в показательной степени с ростом длины волны.
В настоящее время в технике связи в основном применяются кварцевые ОВ, область эффективного использования которых находится в диапазоне длин волн до 2 мкм. На более длинных волнах в качестве материала для волокна используются галоидные, халькогенидные и фторидные стекла. По сравнению с кварцевыми волокнами они обладают большей прозрачностью и обеспечивают снижение потерь на несколько порядков. С появлением ОВ из новых материалов становится реальным создание ВОЛС без ретрансляторов.
Затухание оптического волновода учитывается при расчете энергетического бюджета.
Затухание оптоволоконной линии с учетом потерь на разъемных соединениях и сростках (неразъемных соединениях) определяется по формуле:
![]() (3.1.2)
(3.1.2)
где ![]() и
и ![]() - значение потерь на сростке и разъеме соответственно,
- значение потерь на сростке и разъеме соответственно, ![]() и
и ![]() - количество сростков и разъемных соединений на протяжении оптоволоконной линии длиной L,
- количество сростков и разъемных соединений на протяжении оптоволоконной линии длиной L, ![]() - километрический коэффициент затухания оптического волокна, измеряемый в дБ/км.
- километрический коэффициент затухания оптического волокна, измеряемый в дБ/км.
Тогда энергетический бюджет рассчитывается по формуле:
![]() (3.1.3)
(3.1.3)
где ![]() и
и ![]() - мощность источника оптического излучения и чувствительность фотоприемника в дБ соответственно;
- мощность источника оптического излучения и чувствительность фотоприемника в дБ соответственно; ![]() и
и ![]() - эксплуатационный запас для аппаратуры и для кабеля, (дБ), которые берутся из технических условий (контрактных спецификаций) для оборудования ВОЛС.
- эксплуатационный запас для аппаратуры и для кабеля, (дБ), которые берутся из технических условий (контрактных спецификаций) для оборудования ВОЛС.
Световой сигнал в цифровых системах передачи поступает в световод импульсами, которые вследствие некогерентности реальных источников излучения содержат составляющие с различной частотой. Уширение светового импульса, вызываемое различием времени распространения его спектральных и поляризационных компонент, и называется дисперсией.
Световая волна, распространяющаяся вдоль направления x, описывается уравнением:
![]() (3.2.1)
(3.2.1)
где А - амплитуда световой волны; ![]() - ее угловая частота, k - волновое число.
- ее угловая частота, k - волновое число.
Если взять фиксированное значение фазы волны:
![]() =const, (3.2.2)
=const, (3.2.2)
то скорость перемещения фазы в пространстве или фазовая скорость будет:
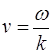 . (3.2.3)
. (3.2.3)
Световой импульс, распространяющийся в ОВ представляет собой суперпозицию электромагнитных волн с частотами, заключенными в интервале Δ![]() , которая называется группой волн вида (3.2.1). В момент времени t в разных точках для разных x волны будут усиливать друг друга, что приводит к появлению максимума интенсивности группы волн (центр группы волн), или ослаблять. Центр группы волн перемещается со скоростью:
, которая называется группой волн вида (3.2.1). В момент времени t в разных точках для разных x волны будут усиливать друг друга, что приводит к появлению максимума интенсивности группы волн (центр группы волн), или ослаблять. Центр группы волн перемещается со скоростью:
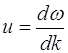 , (3.2.4)
, (3.2.4)
называемой групповой. Заменив k=2π/λ и выразив ![]() , получим соотношение, выражающее зависимость групповой скорости от длины волны:
, получим соотношение, выражающее зависимость групповой скорости от длины волны:
![]() . (3.2.5)
. (3.2.5)
Это и является причиной, приводящей к различию скоростей распространения частотных составляющих излучаемого спектра по оптическому волокну. В результате по мере распространения по оптическому волокну частотные составляющие достигают приемника в разное время. Вследствие этого импульсный сигнал на выходе ОВ видоизменяется, становясь «размытым». Это явление называется волноводной дисперсией, определяемой показателем преломления ОВ и шириной спектра излучения источника Δλ и имеющей размерность времени [5]:
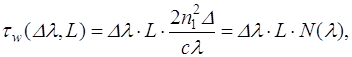 (3.2.6)
(3.2.6)
где Δ - относительная разность показателей преломления сердцевины и оболочки, L - длина ОВ, ![]() - коэффициент волноводной дисперсии, называемый удельной волноводной дисперсией. Зависимость удельной волноводной дисперсии от длины волны показана на рис. 3.2.
- коэффициент волноводной дисперсии, называемый удельной волноводной дисперсией. Зависимость удельной волноводной дисперсии от длины волны показана на рис. 3.2.
Скорость распространения волны зависит не только от частоты, но и от среды распространения. Для объяснения этого явления электроны внутри атомов и молекул рассматриваются в теории дисперсии квазиупруго связанными. При прохождении через вещество световой волны каждый электрон оказывается под воздействием электрической силы и начинает совершать вынужденные колебания. Колеблющиеся электроны возбуждают вторичные волны, распространяющиеся со скоростью с, которые, складываясь с первичной, образуют результирующую волну. Эта результирующая волна распространяется в веществе с фазовой скоростью v, причем, чем ближе частота первичной волны к собственной частоте электронов, тем сильнее будут вынужденные колебания электронов и различие между v и c будет больше, что объясняет зависимость ![]() . В результате смещения электронов из положений равновесия молекула вещества приобретает электрический дипольный момент. То есть при взаимодействии электромагнитной волны со связанными электронами отклик среды зависит от частоты светового импульса, что и определает зависимость показателя преломления от длины волны, которая характеризует дисперсионные свойства оптических материалов:
. В результате смещения электронов из положений равновесия молекула вещества приобретает электрический дипольный момент. То есть при взаимодействии электромагнитной волны со связанными электронами отклик среды зависит от частоты светового импульса, что и определает зависимость показателя преломления от длины волны, которая характеризует дисперсионные свойства оптических материалов:
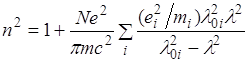 , (3.2.7)
, (3.2.7)
где N - плотность частиц (число частиц в единице объема), m и е – масса и заряд электрона соответственно, ![]() - резонансные длины волн,
- резонансные длины волн, ![]() - вынуждающие осцилляции электрические силы. В широком спектральном диапазоне, включающем обычный ультрафиолет, видимую область и ближнюю инфракрасную область, кварцевое стекло прозрачно и данная формула Солмейера применима с очень высокой точностью [5, 7].
- вынуждающие осцилляции электрические силы. В широком спектральном диапазоне, включающем обычный ультрафиолет, видимую область и ближнюю инфракрасную область, кварцевое стекло прозрачно и данная формула Солмейера применима с очень высокой точностью [5, 7].
Явление, возникновение которого связано с характерными частотами, на которых среда поглощает электромагнитное излучение вследствие осцилляции связанных электронов, и которое определяет уширение длительности светового импульса после его прохождения через дисперсионную среду, называется в технике волоконно-оптической связи материальной дисперсией [5]:
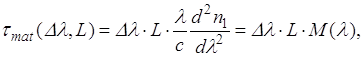 (3.2.8)
(3.2.8)
где коэффициент М(λ) называется удельной материальной дисперсией. На длине волны λ = 1276 нм у кварца величина ![]() , следовательно коэффициент материальной дисперсии M(λ) = 0 (см. рис. 3.2). При длине волны λ > 1276 нм M(λ) меняет знак и принимает отрицательные значения, в результате чего на длине волны (примерно 1310 ± 10 нм для ступенчатого одномодового волокна) происходит взаимная компенсация М(λ) и N(λ). Длина волны, при которой это происходит, называется длиной волны нулевой дисперсии
, следовательно коэффициент материальной дисперсии M(λ) = 0 (см. рис. 3.2). При длине волны λ > 1276 нм M(λ) меняет знак и принимает отрицательные значения, в результате чего на длине волны (примерно 1310 ± 10 нм для ступенчатого одномодового волокна) происходит взаимная компенсация М(λ) и N(λ). Длина волны, при которой это происходит, называется длиной волны нулевой дисперсии ![]() . Обычно указывается некоторый диапазон длин волн, в пределах которых может варьироваться
. Обычно указывается некоторый диапазон длин волн, в пределах которых может варьироваться ![]() для данного конкретного оптического волокна.
для данного конкретного оптического волокна.
Результирующая дисперсия складывается из волноводной и материальной и называется хроматической дисперсией. Дисперсию в оптических волокнах принято характеризовать коэффициентом дисперсии или удельной дисперсией, измеряемом в пс/(нм·км). Коэффициент дисперсии численно равен увеличению длительности светового импульса (в пикосекундах), спектральная ширина которого равна 1 нм, после прохождения отрезка ОВ длиной 1 км. Значение коэффициента хроматической дисперсии определяется как D(λ) = М(λ) + N(λ). Удельная дисперсия имеет размерность пс/(нм·км).
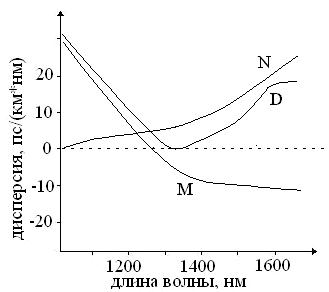 |
Рис. 3.2. Зависимости коэффициентов волноводной, материальной и результирующей хроматической дисперсии от длины волны.
При допущениях, которые исходят из результатов опытов для различных веществ, из выражения (3.2.7) может быть получена приближенная формула зависимости показателя преломления от длины волны:
![]() (3.2.9)
(3.2.9)
где a, b и c - постоянные, значения которых определяются экспериментально для каждого вещества.
Для одномодового ступенчатого и многомодового градиентного оптических волокон для расчета дисперсии применима эмпирическая формула Селмейера [5]:
![]() (3.2.10)
(3.2.10)
Коэффициенты А, В, С являются подгоночными и определяются для каждого материала ОВ экспериментальным путем. Тогда удельная хроматическая дисперсия вычисляется по формуле [5]:
![]() (3.2.11)
(3.2.11)
где ![]() - длина волны нулевой дисперсии, новый параметр S0 =8В - наклон нулевой дисперсии (размерность пс/(нм2·км), а λ - рабочая длина волны, для которой определяется удельная хроматическая дисперсия.
- длина волны нулевой дисперсии, новый параметр S0 =8В - наклон нулевой дисперсии (размерность пс/(нм2·км), а λ - рабочая длина волны, для которой определяется удельная хроматическая дисперсия.
Хроматическая дисперсия связана с удельной хроматической дисперсией простым соотношением:
![]() (3.2.12)
(3.2.12)
К уменьшению хроматической дисперсии ведет использование более когерентных источников излучения, например лазерных передатчиков, и использование рабочей длины волны более близкой к длине волны нулевой дисперсии.
3.3. Распространение световых импульсов в среде с дисперсиейЭлектрическое поле линейно поляризованного светового сигнала, распространяющегося в одномодовом волокне, можно описать следующим образом [6]:
![]() , (3.3.1)
, (3.3.1)
где ![]() - единичный вектор,
- единичный вектор, ![]() - медленно меняющаяся амплитуда (огибающая) светового импульса, представляющая собой комплексный скаляр, который изменяется в направлении z и во времени t, u(х,у) - распределение амплитуды поля в поперечном направлении,
- медленно меняющаяся амплитуда (огибающая) светового импульса, представляющая собой комплексный скаляр, который изменяется в направлении z и во времени t, u(х,у) - распределение амплитуды поля в поперечном направлении, ![]() - постоянная распространения,
- постоянная распространения, ![]() - угловая частота.
- угловая частота.
Распределение амплитуды поля основной моды в поперечном направлении описывается следующим уравнением [6]:
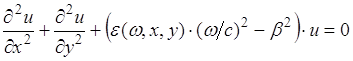 , (3.3.2)
, (3.3.2)
где ![]() (ω)- диэлектрическая проницаемость среды.
(ω)- диэлектрическая проницаемость среды.
В отсутствие в волокне нелинейных явлений рассчитать изменение формы светового импульса в процессе распространения вдоль волокна можно, воспользовавшись преобразованием Фурье [6].
Рассмотрим распространение спектральных
компонент светового сигнала ![]() , получаемых преобразованием Фурье огибающей светового импульса
, получаемых преобразованием Фурье огибающей светового импульса ![]() :
:
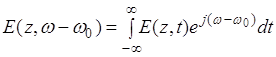 , (3.3.3)
, (3.3.3)
где ![]() - несущая частота.
- несущая частота.
Спектральные компоненты удовлетворяют уравнению:
![]() , (3.3.4)
, (3.3.4)
где ![]() - коэффициент затухания сигнала,
- коэффициент затухания сигнала, ![]() =
=![]() .
.
Решение этого уравнения известно и характеризует затухание сигнала и сдвиг фаз, пропорциональный пройденному расстоянию:
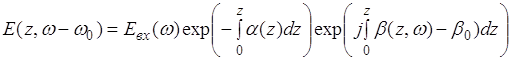 ,(3.3.5)
,(3.3.5)
где Фурье - образ входного светового сигнала имеет вид:
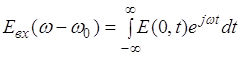 , (3.3.6)
, (3.3.6)
Для однородного волокна выражение упрощается:
![]() (3.3.7)
(3.3.7)
Как следует из выражения (3.3.7), в процессе распространения по волокну разные спектральные компоненты приобретают различный фазовый сдвиг, поэтому Фурье - образ выходного сигнала, прошедшего участок однородного ОВ длиной L, имеет вид:
![]() . (3.3.8)
. (3.3.8)
Форма выходного сигнала может быть получена из Фурье - образа обратным преобразованием Фурье:
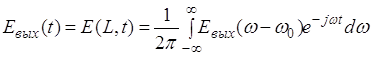 . (3.3.9)
. (3.3.9)
Искажение световых импульсов при распространения в ОВ можно оценить, разложив постоянную распространения β(ω) в ряд Тейлора около несущей частоты ![]() [6]:
[6]:
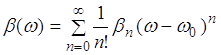 ,
(3.3.10)
,
(3.3.10)
где:
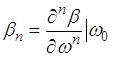 (3.3.11)
(3.3.11)
Выражение (3.3.10), ограниченное первыми четырьмя членами разложения, имеет вид:
![]() . (3.3.12)
. (3.3.12)
Если в разложении (3.3.12) пренебречь степенями выше первой, что соответствует распространению светового импульса по ОВ без искажений, то после подстановки (3.3.12) в (3.3.8), (3.3.9) получается:
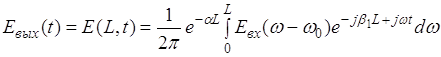 .
(3.3.13)
.
(3.3.13)
Сделав замену переменных ![]() , получим
, получим ![]() . Т.е. в рассмотренном приближении световой импульс затухает, форма его не меняется, и на выходе из волокна он оказывается с временной задержкой
. Т.е. в рассмотренном приближении световой импульс затухает, форма его не меняется, и на выходе из волокна он оказывается с временной задержкой ![]() . Следовательно, групповая скорость распространения светового импульса равна
. Следовательно, групповая скорость распространения светового импульса равна ![]() .
.
Обычно коэффициент при квадрате разности частот не равен нулю, в этом случае световой импульс искажается. Для светового импульса произвольной формы получить аналитическое выражение не удается, но для импульса гауссовой формы (![]() ) аналитическое выражение для выходного импульса имеет следующий вид:
) аналитическое выражение для выходного импульса имеет следующий вид:
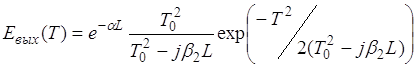 , (3.3.14)
, (3.3.14)
где ![]() - начальная длительность импульса.
- начальная длительность импульса.
Таким образом, гауссовский импульс сохраняют свою форму, но его длительность ![]() , увеличивается [7]:
, увеличивается [7]:
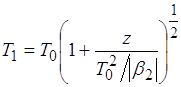 , (3.3.15)
, (3.3.15)
где величина ![]() называется дисперсионной длиной. Выражение (3.3.15) показывает, что при
называется дисперсионной длиной. Выражение (3.3.15) показывает, что при ![]() импульс расширяется. Темп расширения импульса определяется дисперсионной длиной
импульс расширяется. Темп расширения импульса определяется дисперсионной длиной ![]() . При определенной длине световода более короткий импульс уширяется больше, т.к. его дисперсионная длина меньше. При z =
. При определенной длине световода более короткий импульс уширяется больше, т.к. его дисперсионная длина меньше. При z =![]() гауссовский импульс уширяется в
гауссовский импульс уширяется в ![]() раз. Импульс, вначале не имевший частотной модуляции, приобретает ее по мере распространения в ОВ.
раз. Импульс, вначале не имевший частотной модуляции, приобретает ее по мере распространения в ОВ.
Из выражения (3.3.15) следует, что уширение гауссовского импульса, не обладавшего на входе частотной модуляцией, не зависит от знака параметра дисперсии ![]() . Поведение изменяется, однако, если импульс на входе имеет некоторую частотную модуляцию. В случае линейной частотной модуляции гауссовского импульса амплитуда огибающей записывается в виде [6]:
. Поведение изменяется, однако, если импульс на входе имеет некоторую частотную модуляцию. В случае линейной частотной модуляции гауссовского импульса амплитуда огибающей записывается в виде [6]:
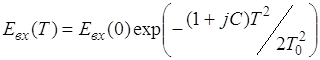 ,
(3.3.16)
,
(3.3.16)
где С - параметр модуляции. Полуширина спектра (на уровне интенсивности 1/е от максимальной) определяется выражением:
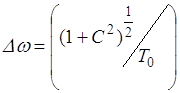 , (3.3.17)
, (3.3.17)
что в ![]() раз больше, чем ширина спектра импульса той же длительности, но без частотной модуляции. Квазимонохроматический импульс без частотной модуляции имеет минимальную длительность, достижимую при заданном спектре. Поэтому световые импульсы без частотной модуляции называются спектрально ограниченными [7].
раз больше, чем ширина спектра импульса той же длительности, но без частотной модуляции. Квазимонохроматический импульс без частотной модуляции имеет минимальную длительность, достижимую при заданном спектре. Поэтому световые импульсы без частотной модуляции называются спектрально ограниченными [7].
Форма прошедшего через оптическое волокно светового импульса с линейной частотной модуляцией (чирпом) имеет вид:
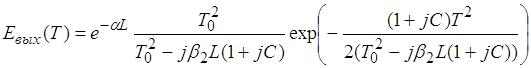 .
.
(3.3.18)
Таким образом, частотно-модулированный (чирпированный) гауссовский импульс сохраняет свою форму при распространении. Длительность импульса ![]() на выходе волокна связана с длительностью на входе соотношением:
на выходе волокна связана с длительностью на входе соотношением:
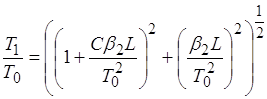 . (3.3.19)
. (3.3.19)
Из выражения (3.3.19) следует, что уширение зависит от знаков параметра ![]() и параметра частотной модуляции С. Гауссовский импульс монотонно расширяется с увеличением расстояния, если
и параметра частотной модуляции С. Гауссовский импульс монотонно расширяется с увеличением расстояния, если ![]() >0.
>0.
Похожие работы
... заданные функции с заданным качеством в течение некоторого промежутка времени в определённых условиях. Изменение состояния элемента (системы), которое влечёт за собой потерю указанного свойства, называется отказом. Надёжность работы ВОЛП – это свойство волоконно-оптической линии обеспечивать возможность передачи требуемой информации с заданным качеством в течение определённого промежутка времени ...
... зондирования, коловорот и др.) КТП-2Г КТП-2БП 1 1 КТП-2П 1 УПТ 1 УПИ 1 1 Комплект устройства для фиксации местоположения соединительных муфт кабельной линии связи УФСМ По согласованию с заказчиком Примечание. Средства измерения 1-5, 10-12, 14-17, 19 и 20 необходимы только в случае исп-я ОК с металл. элементами. 9.1. Электрические проверки основных ...
... к линейным сооружениям ВОЛС. Сразу же после появления волоконно-оптических систем связи в разных странах начали разрабатываться конструкции и способы прокладки волоконно-оптических кабелей, учитывающие особенности монтажа и эксплуатации оптических волокон. К этим особенностям относятся, прежде всего, трудоемкость их соединения и потери полезного сигнала, возникающие при этом. Следовательно, ...
... сигналы. Имеются примеры создания многопозиционных быстродействующих оптических переключателей, которые могут использоваться для оптической коммутации. 1 ОБОСНОВАНИЕ РЕКОНСТРУКЦИИ МАГИСТРАЛИ На участке Ленинск-Амурзет проложено два симметричных кабеля ЗКП 1х4х1,2, по которым осуществляется работа двух аналоговых систем передачи К-60П, ...


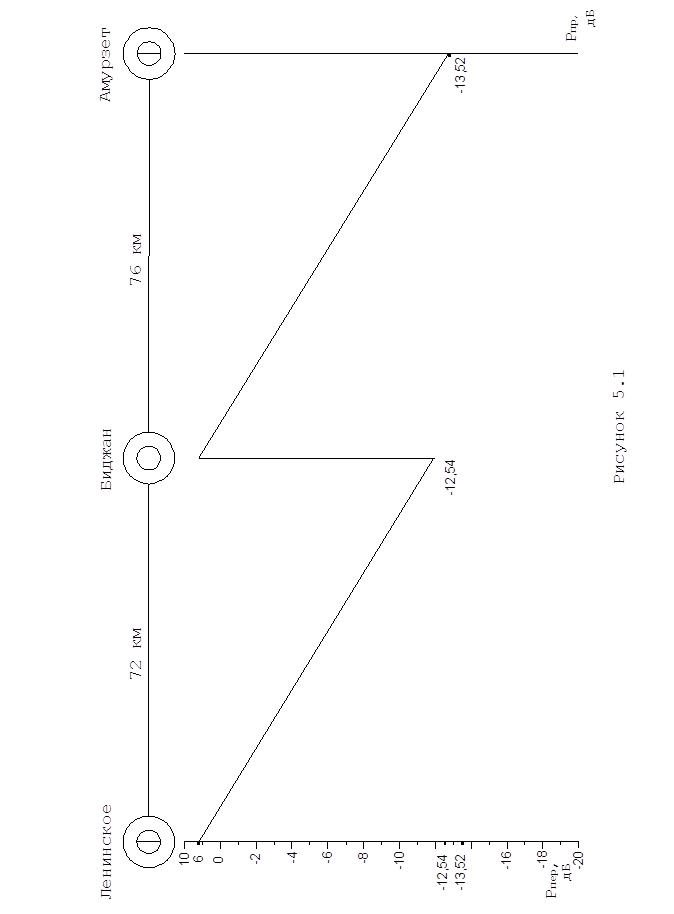


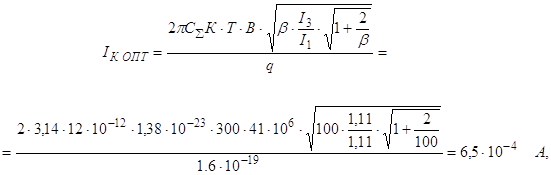
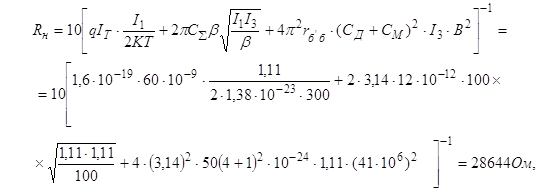
0 комментариев