Ликвидация вертикальных конфликтов межсоединений в канале перед трассировкой

А.В. Мухлаев, С.Н. Щеглов, М.Д. Сеченов

Введение

Низкая временная и пространственная сложность алгоритмов канальной трассировки делает их наиболее приемлемыми в САПР электронных систем, где решаются задачи огромной размерности (несколько миллионов транзисторов). Указанное обстоятельство обусловило повышенный интерес разработчиков САПР к группе канальных алгоритмов и, как следствие, большое число различных типов канальных трассировщиков.

Наибольшее внимание исследователей традиционно привлекала группа канальных алгоритмов, относящихся к безизломным канальным трассировщикам. Подробнее остановимся на указанной группе алгоритмов и введем некоторые основные понятия, так как безизломные канальные трассировщики наиболее приемлемы в последующим причинам:

– позволяют получать решения наиболее быстро ;

– хорошо апробированы и применяются на практике ;

– достаточно качественно и эффективно решают задачу трассировки в двустороннем канале.

1. Классификация, критерии и постановка задачи канальной трассировки

Ввиду того, что задача канальной трассировки в сводится к задаче трассировки горизонтального канала, сверху и снизу ограниченного подлежащими соединению контактами, запишем формальную постановку задачи и дадим традиционные определения плотности и графа вертикальных ограничений (ГВО) (рис. 1).

Пусть задана декартова система координат и на оси Х с ша-гом n отложены точки P^l₁, P^l₂, ...,P^l_n , образующие кортеж B и соответствующие нижнему ряду контактов горизонтального канала, а на некоторой линии m_i (линии m_j откладываются с шагом b ), параллельной оси Х отложены точки P^t₁, P^t₂, ...,P^t_n образующие кортеж Т и соответствующие верхним контактам горизонтaльного канала.

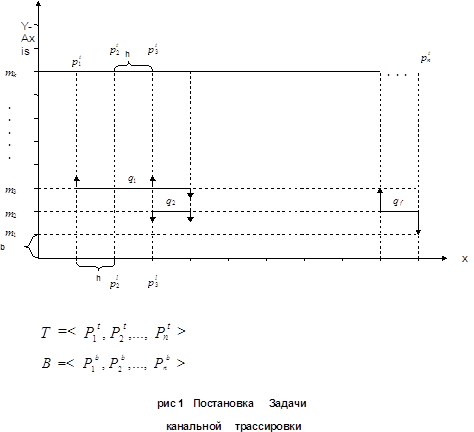
Выделим подмножества P^l_ij,P^t_ij,j=1,f,i=1,f,P^l_j,P^t_i¹0}, каждое из которых составлено из P^l_j и P^t_i равных между собой, т.е. соответствующих одной цепи (f- число цепей). На их основе сформируем множество отрезков Q={q₁,q₂,...,q_n}левые координаты которых равны минимальной координате P^l_jÚP^t_i из соответствующего подмножеcтва Pi-X_q¹_i=min Хрi, а правые координаты-максимальной координате P¹_jÚP^t_j-Xq²_i=maxXp_i

Необходимо распределить q_f отрезков по магистралям таким образом, чтобы требуемое для трассировки число магистралей было минимально: m_k®min и выполнялось ограничение (1)

"(i,j)=1,f:q₁*nq_j=Æ ( 1)

а также ограничения, задаваемые с помощью графа вертикальных ограничений (ГВО), множество вершин которого соответствует P_i,j=1,f ,т.е. соответствует множеству цепей, а две его вершины P_i и P_j соединяются ориентированным ребром, что означает принудительное расположение отрезка q_iвыше, чем q_j в том случае, если

"P^t_ijÎTÞ P^t_ij¹ P^l_ijÎB

Следует отметить, что условие (1) несомненно приоритетно по сравнению с другими критериями трассировки (см. рис. 1), однако, может носить и аддитивный и мультипликативный характер. Отметим, что плотность Ui колонки i канала будем называть число горизонтальных сегментов Sq_i, пересекающих i ко-лонку. Максимальной плотностью Umax назовем Ui :

Широко известны и применяются на практике алгоритмы "Левого края" и раскраски графа ограничений комбинаторные, дающие решения очень быстро. К наиболее эффективным алгоритмам этой группы следует отнести алгоритм Йошимуры, где каждому горизонтальному сегменту цепи q_i ставится в соответствие интегральная характеристика.

Наряду с указанными достоинствами беэизломные алгоритмы обладают и рядом недостатков, при этом один из основных- невозможность решения так называемых циклических конфликтов.

В связи с этим целесообразным представляется разработка подсистемы трассировки, базирующейся на методе систем продукций и содержащей интеллектуализированные процедуры решения циклических конфликтов. В качестве достоинств метода систем продукций отметим:

– модульность;

– понятность работы для операэвора;

– легкость ведения и дополнения БЗ;

– описание правил - продукции на профессиональном языке.

Отметим, что более 70% современных ЭС строятся на основеметода систем продукций /86,87/, и среди них такие известные как MYCIN,OPSS,VIREX,SMALL ТАLK и др.