Навигация
Результаты экспериментов
3.2. Результаты экспериментов
Зависимости времени от числа элементов при разных типах данных (цвет означает соответствующее количество элементов).
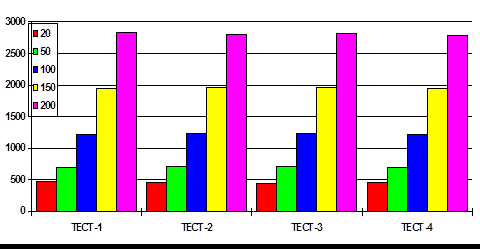
Проведенные исследования показали, что зависимость времени от количества элементов при всех распределениях не достигает квадратной степени при размерах задачи до 200 элементов, что доказывает практическую ценность разработанного алгоритма.
Зависимости качества от числа поколений на разных тестах:(в скобках указаны количества элементов, цвет означает число поколений).
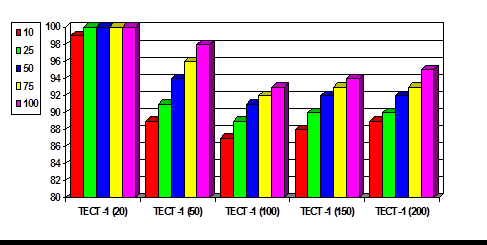
Результаты проведенных исследований показывают, что наиболее плотная упаковка при всех количествах элементов достигается при четвертом типе весового распределения. Второе и третье распределения дают приблизительно равные результаты.
3.3. Сравнение с известными результатами
Было проведено сравнеие разработанного ПаГА с простым ГА (ПГА). Результаты сравнения сведены в таблицу. Они показывают, что ПаГА на всех тестах достиг оптимума и, таким образом, имеет значительное превышение качества решения при незначительном превышении затраченного времени.
| Алгоритм | Кол-во эл-тов | весовое рапред. | размер попул. | кол-во покол. | время решения | качество |
| ПГА | 20 | тест -1 | 20 | 25 | 660 | 0.8544 |
| ПаГА | 20 | тест-1 | 20 | 11 | 517 | 1 |
| ПГА | 20 | тест-2 | 20 | 25 | 660 | 0.8686 |
| ПаГА | 20 | тест-2 | 20 | 9 | 407 | 1 |
| ПГА | 20 | тест-3 | 20 | 25 | 412 | 0.8193 |
| ПаГА | 20 | тест-3 | 20 | 6 | 264 | 1 |
| ПГА | 20 | тест-4 | 20 | 25 | 412 | 0.8418 |
| ПаГА | 20 | тест-4 | 20 | 9 | 410 | 1 |
Список литературы
Brown A.R. Optimal Packing and Depletion. American Elsevier, New York, 1971.
Гэри М., Джонсон Д. Вычислительные машины и труднорешаемые задачи.-М.: Мир, 1982. - 416с.
Yao A.C. New algorithms for bin packing. Report NoSTAN-CS-78-662. Computer Science Dept., Stanford University, Stanford, CA, 1978.
Chi-Chin Yao. A new algorithm for bin packing J. of the ACM, Vol.27, No.2, 1980.
Johnson D.S., Demers A., Ullmans J.D. and oth. Worts-case performance bounds for simple one-dimensional packing algorithms. SIAM J. Comput., vol.3, No. 4, 1974.
Kao C.-Y., Lin F.-T. A statistic approach for the one-dimensional bin-packing problems. In Proceedings of the 1992 IEEE International Conference on Systems, Man, and Cybernetics, vol. 2, 1545-1551. Chicago,IL, 1992.
Garey M.R., Graham R.L., Johnson D.S., Yao A.C. Resource constrained scheduling as generalized bin packing. J. Combinatorial Theory Ser. A21, pp. 257-298.
Goldberg D.E., Genetic Algorithms in Search, Optimization and Machine Larning. Addison-Wesley Publishing Company, Inc. 1989. -354p.
Falkenauer E., Delchambre A. A Genetic Algorithm for Bin Packing and Time Balancing. In: Proc. of the IEEE 1992 International Conference on Robotics and Automation (RA92), Nice, 1992.
Kroger B. Genetic algorithms for bin packing problems. In Stender J. (Ed.) Parallel Genetic Algorithms. IOS Press, Amsterdam, 1993.
Goodman E.D., Tetelbaum A.Y., Kureichik V.M. Genetic Algorithm Approach to Compaction, Bin Packing and Nesting Problems, Technical Report N# 940502, MSU, East lansing,USA, 1994.
Muhlenbein H., Schomisen M., Born J. The Parallel Genetic Algorithm as Function Optimizer. Proc. of the Fourth International Conference on Genetic Algorithms. San Mateo. Morgan Kaufman, 1991. -576p.
Muhlenbein H. Parallel Genetic Algorithms, Population Genetics and Combinatorial Optimization. Proc. of the Third International Conference on Genetic Algorithms. San Mateo. Morgan Kaufmann, 1989. -576p.
Tanese R. Distributed Genetic Algorithms. In J.D.Schaffer (Ed.) Proceedings of the Third International Conference on Genetic Algorithms. Morgan Kaufmann, San Mateo, CA, 1989.
Митропольский А.К. Техника статистических исследований.- М., «Наука», 1971. - 218с.
Применение математических методов и ЭВМ. Планирование и обработка результатов эксперимента: Учеб. пособие./ Под общ. ред. Останина А.Н.- Минск.: Вышэйшая школа., 1989. - 237с.
Адлер Ю.П. Планирование эксперимента при поиске оптимальных условий.-М.: Наука, 1971. - 283с.
0 комментариев