Навигация
Непрерывная модель для гладкой функции яркости
2. Непрерывная модель для гладкой функции яркости
Пусть ![]()
![]() - оценка истинной функции яркости
- оценка истинной функции яркости![]() , которая подвержена сглаживающему преобразованию оптической системы. Поскольку ошибки при получении оценки
, которая подвержена сглаживающему преобразованию оптической системы. Поскольку ошибки при получении оценки ![]()
![]() , как правило, носят интервальный характер, можно с достаточной уверенностью считать, что:
, как правило, носят интервальный характер, можно с достаточной уверенностью считать, что:
![]() |
| ![]()
![]() -
- ![]() |
| ![]() ?.
?.
Здесь? - область определения функции ![]() . Приведенное условие, что значения функции
. Приведенное условие, что значения функции ![]()
![]() и
и ![]() могут отличаться друг от друга не более, чем на значение порога ?.
могут отличаться друг от друга не более, чем на значение порога ?.
Далее степень гладкости функции ![]() в точке
в точке ![]() можно оценить по величине квадрата модуля градиента:
можно оценить по величине квадрата модуля градиента:
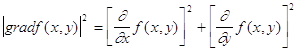 .
.
С учетом этого можно ввести в рассмотрение следующий функционал по критерию гладкости:
 .
.
3. Дискретная модель для выбора наиболее гладкой функции яркости
Будем считать, что значения функции ![]()
![]() известны только в целочисленных точках
известны только в целочисленных точках ![]() ,
, ![]() =
=![]() ,
,
![]() =
=![]() . Тогда необходимо найти значения наиболее «гладкой» функции
. Тогда необходимо найти значения наиболее «гладкой» функции ![]()
![]() в узлах сетки
в узлах сетки ![]() , которая удовлетворяет условию:
, которая удовлетворяет условию:
|![]()
![]() -
- ![]()
![]() |
| ![]() ?,
?, ![]() =1,2,...,N1,
=1,2,...,N1, ![]() =1,2,...,
=1,2,...,![]() . (1)
. (1)
Нетрудно получить дискретный аналог ![]() (
(![]() ) функционала гладкости
) функционала гладкости ![]() , если аппроксимировать квадрат модуля градиента конечными разностями:
, если аппроксимировать квадрат модуля градиента конечными разностями:
![]() |
|![]()
![]()
![]()
![]() -
-![]()
![]() ,
, ![]() |
|![]() ?
? ![]() -
-![]() ,
,
![]() |
|![]()
![]()
![]() .
.
Заменяя интегрирование конечной суммой, получаем:
![]() . (2)
. (2)
Далее необходимо решить задачу на условный экстремум - минимизировать функционал ![]() при условии (1). Это можно сделать методом сопряженных градиентов.
при условии (1). Это можно сделать методом сопряженных градиентов.
Минимизация функционала ![]() с помощью метода сопряженных градиентов
с помощью метода сопряженных градиентов
Нетрудно заметить, что функционал ![]() можно рассматривать как векторную функцию от аргумента
можно рассматривать как векторную функцию от аргумента ![]()
![]()
![]() . Поэтому, учитывая условие (1), функционал
. Поэтому, учитывая условие (1), функционал ![]() необходимо минимизировать в области
необходимо минимизировать в области
![]() .
.
Рассмотрим практическую реализацию метода сопряженных градиентов.
В качестве начального приближения выбирается исходное черно-белое изображение, т.е. ![]() =
=![]() .
.
Пусть на шаге мы имеем сглаженное изображение ![]() . Тогда направление
. Тогда направление ![]() минимизации в методе сопряжения градиентов следует выбрать из условия:
минимизации в методе сопряжения градиентов следует выбрать из условия:
![]() +
+ ![]() . (3)
. (3)
Таким образом, направление минимизации ![]() зависит от предыдущего направления минимизации
зависит от предыдущего направления минимизации ![]() . Мы считаем, что
. Мы считаем, что ![]() =0. При вычислении направления
=0. При вычислении направления ![]() следует учитывать, что точка
следует учитывать, что точка ![]() может лежать на границе области
может лежать на границе области ![]() , т.е. для некоторых значений
, т.е. для некоторых значений ![]() и
и ![]() будет выполняться равенство
будет выполняться равенство
![]() =
= ![]()
![]()
![]() ? (знак «+» или «-»).
? (знак «+» или «-»).
Тогда ![]() координату вектора
координату вектора ![]() следует обнулить, если минимизация вдоль этого направления в любом случае приводит к перемещению точки
следует обнулить, если минимизация вдоль этого направления в любом случае приводит к перемещению точки ![]() за пределы области допустимых значений ? .
за пределы области допустимых значений ? .
При программной реализации положение точки ![]() удобно закодировать:
удобно закодировать:
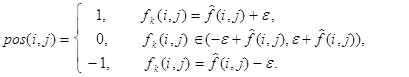
Тогда координату ![]() следует обнулить, если выполняется условие:
следует обнулить, если выполняется условие:
![]() > 0.
> 0.
После того, как вычислено направление минимизации ![]() , функционал
, функционал ![]() минимизируется вдоль данного направления. Для этого необходимо решить оптимизационную задачу
минимизируется вдоль данного направления. Для этого необходимо решить оптимизационную задачу
![]()
относительно параметра![]() . Учитывая, что
. Учитывая, что ![]() - это полином второй степени от многих переменных (положительно определенная квадратичная форма), раскрывая скобки и приводя подобные, получим многочлен второй степени относительно?:
- это полином второй степени от многих переменных (положительно определенная квадратичная форма), раскрывая скобки и приводя подобные, получим многочлен второй степени относительно?:
![]() .
.
Нетрудно заметить, что последняя оптимизационная задача имеет явное решение:
![]() = -
= -![]() .
.
Из логики предлагаемого метода следует, что значение ![]() должно быть положительным. Сглаженное изображение на следующем итерационном шаге определяем по формуле:
должно быть положительным. Сглаженное изображение на следующем итерационном шаге определяем по формуле:
![]() . (4)
. (4)
Однако непосредственно формулу (4) использовать нельзя, поскольку точка ![]() может попасть за пределы области допустимых значений. С учетом этого следует корректировать координаты вектора
может попасть за пределы области допустимых значений. С учетом этого следует корректировать координаты вектора ![]() по формуле:
по формуле:
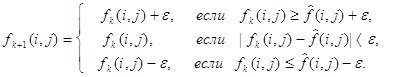
Сходимость данного алгоритма следует оценивать по модулю градиента ![]() , при этом модуль следует рассчитывать только по тем координатам
, при этом модуль следует рассчитывать только по тем координатам![]() , которые не находятся на границе области (в этом случае
, которые не находятся на границе области (в этом случае ![]() ). Аналогично рассчитывается модуль градиента и в формуле (3).
). Аналогично рассчитывается модуль градиента и в формуле (3).
5. Выделение контуров и характерных точек изображения будем называть характерными те точки ![]() изображения, которые являются наиболее информативными, т.е. по которым можно восстановить с некоторой точностью исходное изображение. Нетрудно заметить, что предлагаемый метод сглаживания позволяет выделить характерные точки. Это точки с координатами
изображения, которые являются наиболее информативными, т.е. по которым можно восстановить с некоторой точностью исходное изображение. Нетрудно заметить, что предлагаемый метод сглаживания позволяет выделить характерные точки. Это точки с координатами ![]() , которые являются граничными в том смысле, что
, которые являются граничными в том смысле, что![]() . Данные точки должны определять согласно решению оптимизационной задачи положение всех нехарактерных точек.
. Данные точки должны определять согласно решению оптимизационной задачи положение всех нехарактерных точек.
Нетрудно заметить, что граничными точками будут также точки, определяющие контуры края изображения. В этих точках является большим значение модуля градиента, поэтому в окрестности этих точек не удастся сгладить изображение и значения яркости в этих точках сглаженного изображения окажутся на границе допустимых значений.
Предлагаемая процедура сглаживания позволяет улучшить качественные характеристики методов предварительной обработки изображений, использующих градиент изображения. Отметим в заключение, что предлагаемый метод сглаживания особенно эффективно фильтрует ошибки, возникающие при оцифровке реальных изображений.
Список литературы
Lee D. Coping with discontinuities in Computer Vision: Their Detection, Classification and Measurement// IEEE Transactions on Pattern Analysis and Machine Intelligence, vol.12, № 4, 1990.
Дуда Р.,. Харт П. Распознавание образов и анализ сцен. - М. : Мир, 1976.
Павлидис Т. Алгоритмы машинной графики и обработки изображений. - М.: Радио и связь, 1986.
Похожие работы
... о биологической причинности. Ряд феноменов, которые витализм считал специфическими для биологических объектов (способность к саморегуляции, усложнение строения, достижение одного результата разными способами) рассматриваются в современном естествознании как типичные проявления процессов самоорганизации любых достаточно сложных систем, а не только живых. Н.Бор: “ни один результат биологического ...
... безопасности, привлекаются к административной ответственности, если по действующему законодательству допущенные нарушения не влекут за собой более строго наказания. Анализ I части отчета по преддипломной практике Ночной клуб «Барин» - предприятие общественного питания с широким ассортиментом блюд сложного приготовления, включая заказные и фирменные; вино-водочные, табачные и ...
... переменную. Положительные коэффициенты говорят об усилении стока под влиянием данного фактора, отрицательные – об ослаблении [19]. ГЛАВА 3. Основные особенности регионального климата Рязанской области и его динамики 3.1 Среднемноголетние и экстремальные значения метеорологических величин Рассмотрим данные характеристики на примере метеостанции Елатьма, измерения которой охватывают период ...
... , где мы полностью контролируем все инструменты исследования, в особенности язык, в примитивное общество, где практически невозможно контролировать условия сбора данных и надо освоить новый язык, мы в какой-то мере по необходимости жертвуем методологической строгостью. Но можно быть уверенным, что все эти недостатки методологии исследования с лихвой окупятся теми преимуществами, которые даст нам ...

0 комментариев