Цепь переменного тока с емкостью

2.   Цепь переменного тока с емкостью.

 

В электростатике было изучено устройство конденсатора и его основные свойства. При этом отмечалось, что постоянный ток не проходит в цепи с емкостью, так как диэлектрик конденсатора разрывает цепь. Иначе обстоит дело в цепи переменного тока. Чтобы показать это, составляют цепь с батареей конденсаторов и последовательно включенной с ней лампой накаливания (рис.7).

Лампа горит-значит, в цепи есть ток. При изменении емкости батареи конденсаторов изменяется накал волоска лампы. Это говорит о том, что в данной электрической цепи есть особое (емкостное) сопротивление, которое зависит от емкости.

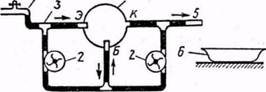
Для разъяснения этого факта полезны гидродинамические аналогии показанные на рис.8.

рис.8

На этих моделях рассматривают возвратно-поступательное движение насоса (или вращение насоса) то в одну, то в другую сторону; при этом упругая перепонка прогибается в соответствующие стороны. Происходит перемещение жидкости в трубах (ток), но жидкость не проходит через перепонку, так же как и заряды в электрической цепи не проходят через диэлектрик конденсатора.

3. Цепь переменного тока с индуктивностью.

 

Наличие индуктивного сопротивления в цепи переменного тока можно продемонстрировать на опыте. Составим цепь из катушки большой индуктивности и электрической лампы накаливания (рис.9).

Рис.9.

С помощью переключателя можно подключить эту цепь либо к источнику постоянного напряжения, либо к источнику переменного напряжения. При этом постоянное напряжение и действующее значение переменного напряжения должны быть равны между собой. Опыт показывает, что лампа светится ярче при постоянном напряжении. Действующее значение силы переменного тока в рассматриваемой цепи меньше силы постоянного тока. Это объясняется явлением самоиндукции. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при нарастании силы тока вихревое электрическое поле тормозит движение электронов и при прошествии некоторого времени сила тока достигает наибольшего значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех значений, которые она бы приобрела с течением времени при постоянном напряжении. Следовательно, максимальное значение силы переменного тока ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и частота приложенного напряжения.

Для индуктивного сопротивления полезна аналогия между индуктивностью в цепи переменного тока и массой материального тела. В случае переменного тока электродвижущая сила самоиндукции имеет место в цепи все время, а не возникает лишь в момент включения и выключения тока, как это было в случае постоянного тока. Наличие этой э.д.с. и объясняет появление индукционного сопротивления.

Обычно рассмотрение цепи переменного тока с индуктивностью проходит без больших затруднений, и аналогия между массой и индуктивностью носит лишь иллюстративный характер. С помощью аналогии объясняют между катушкой индуктивности и источником тока, появление индуктивного сопротивления, а также сдвиг фаз между током и напряжением в данной цепи.

К сожалению, более наглядно гидродинамическую аналогию для этого привести не удается.

4.   Сдвиг фаз между колебаниями тока и напряжения в цепях переменного тока.

Рассмотрим колебания пружинного маятника ( рис.10 ).

Верхнее положение x=A, v=0, a=a_m

x=0, v=v_m, a=0

Нижнее положение x= - A, v=0, a=a_m

Рис.10.

 Легко установить, что между смещением, скоростью и действующей силой имеется сдвиг фаз (рис.11).

Аналогия между механическими и электрическими колебаниями дает возможность показать, что сдвиг фаз между током и напряжением естественен. Вполне допустимо при этом вычертить график и установить соответствие между величинами, характеризующими процессы в электрической цепи (I и U), и величинами, характеризующими процессы в пружинном маятнике (x и v).

Графики аналогичны графику представленным на рис.11, только вместо величин x, v, F ставятся аналогичные им величины q, i, U,то есть  . Для них

i=q^';

Затем поясняют, что при максимальном значении напряжения сила тока в цепи равна нулю и наоборот. Для этого на механической аналогии показывается, что при максимальном значении действующей силы скорость равна нулю, а когда скорость максимальна, равна нулю действующая сила.

§7. Аналогии при изучении постулатов Бора.

Формирование и развитие у учащихся модельных представлений атома как структурной единицы вещества имеет важное научно – познавательное и мировоззренческое значение. В курсе физики 7 класса учащиеся узнают об атомах как о мельчайших частицах вещества, из которых состоят более крупные образования – молекулы. В курсе электричества 8 класса картина меняется: модель атома становится доминирующей. Здесь у учащихся формируется представление об атоме как о сложной динамической системе, состоящей из сконцентрированной в небольшом объеме положительной части – ядра и электронов, движущихся относительно ядра и несущих отрицательный заряд. Планетарную модель атома доказывают опытом Резерфорда по рассеянию α – частиц металлическими пластинками. Известно несколько моделей этого опыта. Например, при описании опыта Резерфорда использована аналогия с зондированием кипы сена с помощью пуль. При этом по траектории пуль можно определить, где спрятаны куски металла. При рассказе о ядерной модели атома применяют аналогию с солнечной системой. Здесь важны образные сравнения – аналогии: масса ядра атома в несколько тысяч раз больше массы электрона (например, масса ядра атома водорода больше массы электрона в 2000 раз), так же как и масса Солнца больше массы отдельной планеты в несколько сотен тысяч раз (например, больше массы Земли в 333000 раз). Другое сравнение : диаметр ядра примерно в 10000 раз меньше диаметра атома; аналогично, диаметр Солнца (13000 км) во много миллионов раз меньше размеров солнечной системы.

Эти сравнения помогают учащимся создать представление о масштабах ядерной модели атома. Но движение электронов относительно ядра более сложнее, чем орбитальное движение планет и оно подчиняется другим законам. Ядерную модель атома затем используют для объяснения электризации тел, явления электропроводности, при изучении электрического тока в металлах и электролитах. О дальнейшем развитии планетарной модели атома рассказывают после изучения фотоэффекта.

Для объяснения закономерностей фотоэффекта вводят представление о дискретности светового излучения, а также понятие о фотоне как элементарной частице света с энергией Е=hν. Отсюда возникает вопрос: является ли дискретность энергетических состояний свойством, характерным лишь для излучающих твердых тел, или же эта дискретность присуща любым атомным системам?

Подобные рассуждения привели в 1913 году И. Бора к предположению о неприменимости максвелловской электродинамики к электронам, движущимся в атомах. В основу своей теории Н. Бор положил следующие постулаты:

1)   в атоме происходят движения электронов по некоторым стационарным круговым орбитам без излучения;

2)   стационарными будут те орбиты, для которых момент количества движения электрона mvR равен целому кратному величины h/2π, то есть

mv_nR_n=nh/2π , где n=1, 2, 3….

3)   излучение и поглощение света атомами происходит при переходе электронов с одних стационарных орбит на другие.

Планетарная модель атома в теории Бора “модернизирована”, то есть электроны могут перескакивать с орбиты на орбиту, когда атом переходит из одного стационарного состояния в другое.

Так, при изложении вопроса об излучении света атомом существует аналогия с реальным макропроцессом—вылетом стрелы из лука.

 Оба процесса возможны только в том случае, если уча­ствующие в них объекты (атом, лук) нахо­дятся в возбужденном состоянии (в послед­нем случае под «возбуждением» понимается натяжение тетивы). Тетива и атом в конечном счете возвращаются в невозбужден­ное состояние (ему соответствует наименьшее из возможных значение энергии); при этом соблюдается закон сохранения энергии (потенциальная энергия упруго деформиро­ванной тетивы переходит в кинетическую энергию стрелы, а энергия возбуждения ато­ма «уносится» фотоном: Е₂-Е₁=hν.

Однако между этими явлениями есть различие:

1)   при натяжении тетивы ей может быть со­общена любая энергия, т. е. ее энергия мо­жет изменяться непрерывно; для возбужде­ния атома ему нужно сообщить определен­ную порцию (квант) энергии, соответствую­щую разности уровней энергии, между кото­рыми осуществляется «переход» электрона в рамках модели Резерфорда—Бора;

2)   воз­вращаясь в «невозбужденное» состояние, те­тива «проходит» все промежуточные состоя­ния (значения энергии),, таких состояний, очевидно, бесчисленное множество; электрон же в атоме переходит из любого возбужден­ного состояния в нормальное либо одним, либо несколькими последовательными скач­ками, минуя промежуточные значения энер­гии;

3)   стрела, символизирующая световой квант, существовала до возбуждения тетивы и до вылета покоилась относительно лука, при вылете она постепенно набирала ско­рость от нуля до какого-то максимального значения; фотон “рождается” лишь благодаря переходу атома из состояния с большей энергией в состояние с меньшей энергией, т.е. переходу электрона на более низкую орбиту; покоящегося же (относительно любой системы отчета) фотон не существует: фотон сразу приобретает скорость света.

Постулаты Бора дают возможность вычислить полную энергию атома исходя из уравнений:

mvR=nh/2π (1)

(2)

  (3)

V=nh/2πmR; n²h²/4π²mR³=Ze²/R²

R=n²h²/Ze²4π²m

E=- (4) где n =1, 2, 3…..

Полную энергию атома при определенном стационарном состояии называют энергетическим уровнем. Вычисляя значения E при n=1, E при n=2 и т. д., получаем ряд значений энергии:

Е₁=-13,53 эВ; Е₂=-3,4 эВ; Е₃=-1,5 эВ; Е₄=-0,8 эВ и т.п.

При n=∞ Е_∞=0.

После вычислений строим график (рис.5.):

Рис.5.

Ось энергии в этом графике берут вертикальной, за начало отсчета выбирают энергию атома, когда его электрон удален в бесконечность – это нулевой уровень энергии атома. Так как энергия атома орбитальна, то все последующие значения энергии будут ниже нулевого уровня. Минимум энергии (E₁=-13,53эВ) атома соответствует невозбужденному его состоянию, когда электрон находится на наиболее близкой к ядру орбите. Выбирают масштаб таким образом, чтобы потом легко было разделить отрезок, соответствующий расстоянию между уровнями E_∞ и E₁ на 4, 9, 16 и т. д., равных частей. Построенное таким образом изображение значений энергии атома в различных его состояниях называют энергетической моделью атома.

Энергетическая модель атома дает ряд объяснений:

а) объяснение происхождения линейчатых спектров.

Линейчатый спектр испускания объясняют переходом атома, находящегося в возбужденном состоянии, с высшего энергетического уровня на более низкий. Например, при переходе со второго энергетического уровня на первый энергия атома уменьшается на Е₂-Е₁=1,77 эВ; при этом испускается фотон света с длиной волны, равной

λ=

Линии поглощения в спектре атома образуются в результате перехода атома с энергетического уровня, соответствующего невозбужденному состоянию атома, на более низкий уровень за счет энергии получаемой из вне. Так как атом обладает вполне определенными, дискретными значениями энергии, то и длины волн излучаемого или поглощаемого света вполне определены. Чем больше разность энергий уровня атома, тем меньшей длины волны испускается свет.

б) Объяснение люминесценции.

Механизм флюоресценции показан на рис.6.

Рис.6.

Фотон с энергией hν₁₅ поглощается молекулой, переводя ее из состояния с энергией Е в возбужденное состояние Е₁ . Обратный переход может идти прямо (пунктирная линия) или в виде каскадного процесса, когда испускаются различные фотоны с энергиями hν₅₄ , hν₄₂ , hν₂₁ , причем энергия поглощенного фотона (hν₀) может оказаться меньше суммарной энергии испускаемых фотонов (hν) . Часть энергии фотона (А) передается соседним молекулам и затрачивается на различные внутримолекулярные процессы. Поэтому справедливо равенство:

hν = hν₀ –A

Откуда ν < ν ₀, λ > λ₀ ,то есть длина волны испускаемого света при люминесценции меньше длины волны падающего света.

Фосфоресценцию наблюдают в кристаллах, где центрами свечения являются атомы, ионы или группы их. Электрон, возбужденный поглощаемым светом, нередко отделяется от центра свечения. При возвращении электрона на прежнее место свечение возобновляется. Так как скорость перемещения электрона в кристалле мала, то свечение может продолжаться длительное время.

Поэтому при изучении энергетических диаграмм полезно сопоставить их с планетарной моделью Резерфорда – Бора, обратив внимание на важные моменты:

1.    В энергетической модели орбит нет, указываются лишь энергии атомов в определенных состояниях.

2.    В соответствии с этим речь идет не о перескоках с орбиты на орбиту, а о переходе атомов из состояния с большей энергией в состояние с меньшей энергией (при излучении) или же наоборот (при возбуждении).

3. Расстояние между орбитами имеют геометрический смысл, а между уровнями – энергетический; поэтому говорить о скачках электрона с уровня на уровень недопустимо.

Таким образом данная аналогия помогает учащимся лучше разобраться и понять постулаты Бора и энергетическую модель атома.

ГЛАВА 3. Изучение аналогий на факультативах,

кружках и спецкурсах.

 

§ 8. Волчок и магнит.

Рассмотрим пример, который заключается в запуске волчка. При запуске волчка, мы любуемся его кружением, удивляемся его устойчивости и нам хочется разгадать его тайну. Почему неподвижный волчок не может стоять на острие своей оси, а приведи его в быстрое движение – и, словно перед тобой совсем другой предмет, он стойко держится, вращаясь вокруг вертикальной оси. Мало того, волчок упорно сопротивляется попыткам упорно вывести его из этого положения. Если попытаться толкнуть его, вывести волчок из вертикального положения, опрокинуть, но волчок и после толчка продолжает кружиться, описывая своей осью кони­ческую поверхность (рис. 1).

Рис.1.

Если рассмотреть опыт с вращающейся цепью и заставить ее стоять, как твердый обруч, покажется смеш­ной фантазией, но сообщите цепи быстрое вращение, надев ее на вращающийся шкив, и затем сдвиньте в сторону, дайте ей со­скользнуть на стол, и она «побежит» по столу так же, как если бы была твердым кольцом.

Механика дает объяснение этому удивительному явлению. Для этого надо знать закон сохранения момента импульса. Для вращательного движения справедлив закон сохранения момента импульса: L = Iw = const. где L — момент импульса; I — момент инерции, характеризующий инерцию вращательного движения, w — угловая скорость. Только под действием внешних сил, например трения, катящаяся цепочка может уменьшить скорость враще­ния и тогда, потеряв форму, упадет на стол. То же относится и к волчку.

Мы познакомились с одним свойством волчка—сохранением направления оси волчка. Обратимся ко второму важному его свойству. Лучше всего оно обнаруживается в следующем опыте (рис. 2).

 

Рис.2.

Сплошная латунная шайба К. с утолщенным ободом надета на стальную ось А, вокруг которой она может вращаться внутри латунного кольца . Если намотать на ось шнурок и бы­стро потянуть его, то шайба придет в быстрое вращение. При­лив D на кольце R имеет снизу углубление, которым весь волчок может быть надет на стальное острие штатива. Если при этом не поддерживать прибор рукой, то он под действием силы тяже­сти опрокинется и упадет. Если же, прежде чем убрать руку, привести прибор во вращение, то ось волчка с его кольцами как бы повиснет в горизонтальном положении, причем вся система будет поворачиваться вокруг вертикальной оси штатива. Это вращение получило название прецессии. Прецессия возникла как результат действия силы тяжести и стремления вращающегося волчка сохранять направление оси.

В 1852 г. французский физик Фуко обнаружил, что горизон­тальная ось вращающегося волчка устанавливается в направле­нии север — юг, подобно магнитной стрелке компаса. С той раз­ницей, что ось волчка устанавливается в плоскости географиче­ского меридиана, а стрелка компаса в плоскости магнитного ме­ридиана, который, как известно, не совпадает с географическим.

Объясним это удивительное свойство волчка. Для простоты представим, что наш гироскоп расположен на экваторе в точке А (рис. 3), причем его ось ориентирована с востока на запад. Так как Земля вращается, то через некоторое время точ­ка А перейдет из положения 1 в положение 2. Ось гироскопа, как мы знаем, стремится сохранить прежнее направление, но действие силы тяжести приводит ее снова в горизонтальное по­ложение. Совместное действие силы тяжести и вращения вызы­вает прецессию. Ось поворачивается до тех пор, пока не устано­вится параллельно земной оси, в плоскости меридиана с севера на юг. После этого прецессия прекращается, так как при про­должающемся вращении Земли ось гироскопа будет перемещать­ся параллельно самой себе, а прецессия наблюдается при попыт­ке изменить направление оси. Все вращающиеся тела, например маховые колеса двигателей, стремятся повернуть свои оси по на­правлению к Полярной звезде.

A 1

экватор

2

Рис.3.

Тысячелетиями люди удивлялись чудесным свойствам магни­та, но не могли разгадать его тайну, так как не знали законов волчка и строение атома.

Первое научное сочинение о магнетизме принадлежит англий­скому врачу Гильберту, написавшему в 1600 г. книгу «О магни­те, магнитных телах и большом магните—Земле». Здесь впер­вые уточняется понятие полюсов магнита, а также делается по­пытка понять строение магнита: если разделить магнит на части, то получится множество маленьких магнитов. Следовательно, магнит состоит из множества маленьких магнитиков.

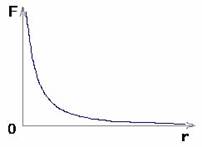
Только в 1785 г. французский военный инженер Кулон, используя изобретенные им крутильные весы, исследовал взаимо­действие магнитных полюсов и доказал, что оно подчинено зако­ну обратных квадратов, расстояния.

Однако природа магнита продолжала оставаться таинствен­ной. Только аналогия притяжения и отталкивания магнитных полюсов и электрических зарядов наводила на мысль о родстве этих двух явлений. Лишь после обнаружения Эрстедом на опыте действия электрического тока на магнитную стрелку и уточне­ния Ампером законов этого, действия мысль о взаимосвязи элект­ричества и магнетизма была подтверждена. Ампер выдвинул теорию, по которой магнит состоит из маленьких, элементарных круговых токов, но круговой ток. как известно, обладает магнит­ными полюсами (рис. 4). Фарадей и Максвелл разработали учение о магнитном поле.

N

S

Рис.4.

 Еще Фарадей установил, что все вещества можно разделить. на две группы — парамагнитных и диамагнитных веществ и что нет материалов, безразличных к магнетизму. Правда, магнитные свойства большинства тел очень слабо выражены и для их обна­ружения приходится воздействовать очень сильными магнитны­ми полями на маленькие и легкие образцы исследуемых мате­риалов. Подвешивая стержень из висмута между полюсами силь­ного электромагнита, можно увидеть, что стержень устанавли­вается перпендикулярно направлению линий индукции магнитного поля, тогда как стержень из алюминия располагается параллельно этим линиям. Висмут диамагнитен, алюминий пара­магнитен (в переводе с греческого пара — значит вдоль, диа — поперек, через).

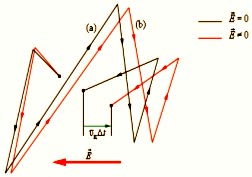
Лишь в наши дни явления диа- и парамагнетизма получили свое объяснение в электронной теории. Начнем с диамагнетиз­ма. Его происхождение связано с движением электронов вокруг ядра атома по орбите (назовем это движение орбитальным). Электрон, обращающийся вокруг ядра, можно уподобить волчку, и подобно тому как поле тяготения вызывает прецессию волчка, противодействующую силе тяжести, так внешнее магнитное поле вызывает прецессию вращающегося вокруг ядра электрона, про­тиводействующую магнитному полю. Так как в любом атоме лю­бого вещества происходит орбитальное движение электронов, то диамагнетизм свойствен всем видам вещества. Но диамагнитные свойства очень слабы и во многих случаях они перекрываются парамагнитными свойствами. От чего же зависят парамагнитные свойства? Дело в том, что, кроме орбитального движения, элект­ронам присуще еще и вращательное движение вокруг их собст­венной оси. Для наглядности принято сравнивать движение электрона вокруг собственной оси с движением Земли вокруг оси (при одновременном ее движении по орбите вокруг Солнца). Таким образом, электрон уподобляется волчку, и его движение получило название «спин» (от английского глагола to spin — запускать волчок). Надо при этом иметь в виду, что это всего лишь полезный, наглядный образ. Современная физика отказа­лась от представления об электроне, как о каком-то вращающем­ся шарике, однако спин все-таки существует, и мы будем поль­зоваться этим наглядным образом электрона-волчка, обладаю­щего магнитными свойствами.

В зависимости от направления вращения условно различают положительный спин и отрицательный. Два спина с противоположными знаками друг друга «нейтрализуют» (рис. 5).

S

N

N N

S S

Рис.5.

 Если каждому электрону с положительным спином соответ­ствует в атоме электрон с отрицательным спином, то магнитные свойства, зависящие от спинов, нейтрализуются и остается лишь магнетизм, зависящий от орбитального движения электронов. Вещества из таких атомов диамагнитны.

Но во многих случаях числа положительных и отрицатель­ных спинов не уравновешены, тогда атом обладает результирую­щим спином и соответствующим магнитным моментом. Рису­нок 6 иллюстрирует схему атома железа.

- электрон со спином +

- электрон со спином -

Рис.6.

Электроны на оболочках К, L, и N спарены (эти оболочки заселены парами электронов с противоположно ориентированными спинами), тогда как на оболочке М имеются непарные электроны, дающие нескомпонсированный спин — спин атома. То же, только в более слабой степени, можно сказать и о любом парамагнетике.

Рис.7.

Тепловое движение приводит спины атомов в беспорядочное расположение, и парамагнитные свойства вещества обычно не проявляются (рис. 7 слева). Но если поместить такое вещест­во во внешнее магнитное поле, то спины атомов в результате прецессии ориентируются приблизительно вдоль линий индук­ции внешнего магнитного поля (как гироскоп вдоль меридиана) и вещество проявляет свойства парамагнетика (рис. 7 справа).

Особую группу составляет небольшой класс веществ — фер­ромагнетики, названные по их главному представителю — желе­зу. По современной теории кристалл железа состоит из отдель­ных микроскопических областей (доменов), в каждой из которых спины атомов уже расположены (без участия внешнего поля) в направлении кристаллических осей (вспомните анизотропию кристаллов). В ненамагниченном железе домены ориентированы так, что суммарное магнитное поле их равно нулю (рис. 8).

рис.8.

Поднося к куску железа магнит или помещая его в магнитное поле, мы вызываем определенную ориентацию доменов и появление магнитных свойств — железо становится магнитом. Неакку­ратным обращением вы можете испортить этот магнит, если будете, например, ронять его или ударять по нему, так как при ударах наведенный порядок доменов нарушается. Наоборот, вы можете усилить магнитные свойства магнита, если замкнете его полюсы железной пластинкой, к середине которой подвесите маленькую коробочку, и будете постепенно, день за днем, добав­лять в коробочку грузы (песок). Так вы сможете «воспитать» ваш магнит, и он будет поднимать значительные тяжести.

При нагревании магнит теряет свои магнитные свойства. Существует температура (температура Кюри), при которой ферромагнетик совершенно размагничивается и превращается в парамагнетик. Для железа эта температура равна 770°C.

Магнитные качества ферромагнетиков в сильной степени за­висят от примеси других веществ к железу. Это свойство исполь­зуется в технике, когда желают получить более прочные постоян­ные магниты или, наоборот, материал, способный легко терять свои магнитные свойства или перемагничиваться в обратном на­правлении (сердечники трансформаторов, моторов, генераторов).

Технология ферромагнитных материалов использует еще особую группу материалов, называемых ферритами. Они пред­ставляют собой полупроводники и состоят из смеси оксидов железа с оксидами некоторых других металлов (марганца, ко­бальта, никеля, меди, магния). Порошки этих оксидов тщатель­но смешивают, спрессовывают и придают им .различную, форму (палочек, колец и др.). Ферриты обладают очень большим элект­рическим сопротивлением и большой магнитной проницае­мостью — эти свойства и обуславливают их широкое применение. Ферритова машина маленькая - палочка – позволяет заменять длиннные антенны в портативных радиоприемниках, транзисторах. Ферритовы кольца используют в «памяти» электронновычислительных машин.

§9. СВЕТ И ГЛАЗ

 

Немецкому физику и физиологу Гельмгольцу принадлежит фраза: «Если бы оптик принес мне столь несовершенный инстру­мент, как человеческий глаз, я бы тотчас выбросил его за дверь. С такой суровой оценкой можно было бы согласиться лишь в том случае, если судить о глазе только как об оптическом приборе. Совсем иное будет суждение, если мы будем рассматривать всю совокупность зри­тельного органа и будем оценивать глаз как один из основных анализаторов (в свете учения И. П. Павлова), воспринимаю­щих действия раздражителей внешнего мира на нашу нервную систему.

Сколько волнующих слов сказали поэты о глазах, черных, голубых... Сколько художников пытались передать их очарова­ние. Но разве не связан с глазом весь раздел «Геометрическая оптика». Основ­ное понятие геометрической оптики - луч. Пронизывающие чащу леса или вырывающиеся из-за туч потоки света действительно создают представление о лучах. В темном зрительном зале кино­театра из окошечка кинобудки вырывается сноп света, воспри­нимаемый нами как расходящийся конус лучей. Но, конечно, это не собрание лучей, это пучки света, а луч - это идеализирован­ное понятие, геометрическая линия. Пучок света - это физика, луч - геометрия. Геометрическое понятие прямой линии тесно связано с понятием луча, a значит, со свойством нашего глаза. Когда плотник проверяет прямолинейность кромки оструганной доски, он смотрит вдоль нее по лучу зрения. Образо­вание теней и солнечных пятен связано с прямолинейным рас­пространением световых пучков.

Солнечные пятна представляют собой изображения Солнца, получившиеся при прохождении пучка света через малые от­верстия. Камера-обскура — исстари известный оптический при­бор. Для получения четких изображений необходимо только подобрать размер отверстия. Уменьшение его ведет к по­лучению более отчетливых изображений, так как узкие пучки света от отдельных точек предмета не накладываются друг на друга. При чрезмерном уменьшении отверстия изобра­жение снова становится туманным. Здесь кончается геометриче­ская оптика и проявляется волновая природа света. Речь идет о дифракции.

 Человеческий глаз тоже представляет собой устрой­ство, по принципу действия схожее с фотоаппаратом. Через зра­чок-отверстие в радужной (окрашенной) оболочке глаза, ко­торое, подобно диафрагме фотоаппарата, может сужаться или расширяться, в зависимости от яркости освещения, лучи света проходят через хрусталик и дают изображение на сетчатой обо­лочке глаза.

Как изменится изображение на фотографической пластинке или на экране при показе диапозитивов при помощи проекцион­ного фонаря, если закрыть половину объектива?

Диафрагма позволяет получить более резкое изобра­жение, способствует увеличению резкости изображения на сет­чатке, а следовательно, и более отчетливому видению и сужению зрачка нашего глаза. Вот интересное подтверждение этому: не прибегая к лупе, можно разобрать мелкую печать, если страница ярко освещена солнцем. Яркое освещение заставляет зрачок суживаться, и изображение становится более резким. Люди, чи­тающие обычно в очках (дальнозоркие), могут в случае необ­ходимости прочитать написанное без очков. Оставив маленькую дырочку между сжатыми пальцами, надо смотреть одним глазом на страницу, зажмурив при этом другой. Тогда из туманных строчек страницы выступит отчетливо видимая часть строки.

Если посмотреть сбоку на человеческий глаз, то видна выпук­лость. Это роговая оболочка. За ней расположена радужная оболочка. Между роговой и радужной оболочкой находится «водянистая жидкость», далее хрусталик, и, наконец, студени­стое «стекловидное тело», которые образуют оптическую систе­му глаза. Подобно фотоаппарату, глаз наводится на резкость, и на сетчатке получается четкое изображение рассматриваемого предмета. Это достигается изменением кривизны хрустали­ка (рис. 1).

Рис.1

 Окружающие хрусталик мышцы могут сжимать или растягивать хрусталик и тем самым изменять в известных пределах, его фокусное расстояние.

Сходство в получении зрительных изображений в глазу с фотографическим процессом мы находим и в химических явле­ниях на сетчатке. Они аналогичны процессам, которые происхо­дят в светочувствительной эмульсии пленки. На фотографиче­ской пленке световое изображение снимаемого предмета вызыва­ет разложение бромида серебра в светочувствительном слое. В глазу под действием света происходит разложение (обесцве­чивание) особого вещества - зрительного пурпура, приготовля­емого светочувствительным слоем сетчатки (пигментным эпите­лием). Более яркие места светового изображения вызовут боль­шее разложение пурпура, темные - меньшее. Вследствие этого на сетчатке, как и на фотопленке, получается изображение.

На задаваемый обычно вопрос, почему мы не видим предме­ты «вверх ногами», раз изображение на сетчатке получается обратное, можно было бы и не отвечать, так как этот вопрос со­держит в себе ошибку. Самый короткий ответ был бы тот, что мы видим не изображение на сетчатке (которое действительно обратное), а предметы во внешнем мире. Что такое верх и низ? Это понятия относительные. Люди, находящиеся на противопо­ложной стороне земного шара, по отношению к нам ходят «вверх ногами». Бесспорным, выработанным всей практикой жизни бу­дет определение направления «вниз» как направления силы тя­жести. Поднимая руку и совершая при этом работу против силы тяжести, мы указываем рукой вверх. Практика позволяет нам всегда устанавливать, где верх, а где низ предметов. Это одна из тех поправок, которые опыт и мозговая деятельность вносят в расшифровку зрительных впечатлений.

Изучая различные оптические системы, мы схематически изо­бражаем ход лучей и делаем построение предмета и его изобра­жения. При этом нередко говорят о том, что через оптическую систему мы рассматриваем мнимое изображение предмета. Вспомним привычное объяснение получения изображения от предмета, помещенного между главным фокусом и линзой. Мнимое изображение в этом случае получится там, где пере­секутся продолжения расходящихся лучей, попадающих в глаз (рис. 2).

мнимое изображение объекта

b

B

a .F A

объект

Рис.2.

Рассмотрим подробнее ход лучей от предмета. Расходящиеся после прохождения линзы световые лучи фокусируются оптиче­ской системой глаза на сетчатке (рис. 3).

 

А

F В

Рис.3.

В результате мы получаем зрительное впечатление. При изменении положения предмета оптическая система глаза все равно будет фокусиро­вать лучи на сетчатке. Только для этого хрусталику потребуется изменить свою кривизну (это делают мышцы, окружающие хрусталик). Такое приспособление глаза к разным расстояниям до рассматриваемых предметов называется аккомодацией.

Но как быть с изображением в плоском зеркале? В любом учебнике физики приводится чертеж образования мнимого изо­бражения за плоским зеркалом. Чертеж правилен. Но вы сейчас смотрите только на чертеж, а не в зеркало. На чертеже получи­лось мнимое изображение. Значит, его нельзя получить на экра­не, на фотографической пластинке, на сетчатке глаза. Рассмотрим следующий опыт.

Поставим против окна зеркало, между зеркалом и окном — двояковыпуклую линзу. Передвигая лист белой бумаги, вы очень скоро сумеете получить перевернутое изображение окна; если хотите получить свой автопортрет, вы можете сфотографироваться в зеркале. А так как глаз подобен фото­камере, то, следовательно, и на сетчатке глаза получается дейст­вительное, а не мнимое изображение предметов, отражающихся в зеркале. Ход лучей, поясняющий сказанное, вы увидите на ри­сунке 4.

Необходимо сделать еще несколько замечаний, касающихся геометрической оптики. Допустим, вы рассматриваете в лупу мелкую печать. Вы приближаете глаз и лупу к бумаге до тех пор, пока не получите наиболее ясное изображение. В этот мо­мент хрусталик аккомодирован на «расстояние наилучшего зре­ния». Это расстояние обычно принимают равным 25 см, хотя у разных лиц и в разном возрасте способность к аккомодации раз­лична. Хотите знать, во сколько раз увеличивает лупа? Если хрусталик аккомодирован на расстояние наилучшего зрения, то ответ дает формула:

где Г - увеличение лупы, F - фокусное расстояние, измеряемое в сантиметрах. При ненапряженном глазе увеличение, даваемое лупой, равно

Но как определить F? В солнечный день это можно сделать, собрав лучи солнца в фокус и измерив расстояние от лупы до него. Если солнца нет, то надо навести линзу на далекий пред­мет (ландшафт за окном) и получить резкое его изображение на бумаге. Расстояние от линзы до изображения можно считать практически равным фокусному расстоянию. Действительно, в формуле линзы

для далеких предметов (d=¥) дробь  исчезающе мала, и тогда

 или f=F (расстояние до изображения равно фокусному расстоянию линзы).

Описанный прием нахождения фокусного расстояния двояко­выпуклой линзы позволит решить еще одну интересную и полез­ную задачу. Пусть вы задумали построить себе самодельный телескоп из очковых стекол. Но тогда понадобится прежде всего знать номер очков (для дальнозорких). Номер очков показывает их оптическую силу, или величину, обратную фокусному рас­стоянию:

Оптическая сила выражается в диоптриях. 1 дптр — это опти­ческая сила линзы, у которой F==1 м.

 Поэтому, измерив F выше описанным путем, вы определите и номер очков. Например, если F=50 см==0,5 м, то D =2 дптр, или номер очков +2.

Для изготовления телескопа вам понадобится для объектива стекло +2 или +1, т. е. линза с фокусным расстоянием 50 или 100 см. Можно вместо очкового стекла приобрести в магазине фототоваров соответствующую насадочную линзу для фотоаппа­рата. Для окуляра надо взять какую-нибудь сильную линзу с фокусным расстоянием равную примерно 2 см. Тогда телескоп будет увеличивать в

 Объектив и окуляр укрепите в раз­движной картонной трубке (рис. 5), внутреннюю поверхность которой надо вычернить тушью. Исключительно важно сделать для телескопа держатель (можно использовать штатив для фото­аппарата).

Для суждения о размерах предмета и для лучшего различения его подробностей важен «угол зрения»—угол между лучами, проведенными от крайних точек предмета к центру хрусталика. Чтобы сделать видимыми неразличимые ранее детали, надо по­дойти ближе к предмету. Тогда угол зрения и изображение на сетчатке увеличатся. Насколько близко можно подойти к пред­мету? Для нормального глаза это определяется расстоянием наи­лучшего зрения — 25 см. При меньших расстояниях глаз с тру­дом аккомодирует, а без аккомодации он видит лишь размытое изображение. Но выпуклость глаза можно усилить, поставив перед ним двояковыпуклою линзу. Это позволит приблизить глаз к предмету и получить резкое изображение без аккомодирующего усилия. В этом и состоит назначение лупы — она по­зволяет увеличить угол зрения.

­

Заключение.

Рассмотренные аналогии позволяют более глубоко проникнуть в процесс обучения физики средней школы, что в свою очередь дает учащимся лучше понимать физические законы и процессы.

В данной работе рассмотрена лишь небольшая часть аналогий, которые можно использовать на уроках физики и на факультативных занятиях в средней школе.

Я считаю, что аналогии лучше всего рассматривать не только на уроках физики, но и придавать им так же большое значение на факультативных занятиях, кружках, спецкурсах для учащихся, которым трудно поддается изучаемый материал и для учащихся, которые хотят более глубоко понять физические процессы, явления и понятия.

Таким образом метод аналогии рассматривает новые вопросы, сопоставляемые с изученными ранее.

Список литературы.

1. Аванесов Ю. Г. Использование аналогий при изучении постулатов Бора .

//Физика в школе// №2, 1983 г.

2. Блудов М. И. Беседы по физике. М. “ Просвещение “, 1985 г.

3. Ванюшенков И. С., Каненецкий С. Использование аналогии при изучении транзисторов. //Физика в школе// №3, 1991 г.

4. Дроздов В. Г. Аналогии при изучении колебательных систем в 10 классе .

//Физика в школе// №3, 1991 г.

 5. Каненецкий С. Е., Солодухин Н. Н. Модели и аналогии в курсе физики средней школы . М. “ Просвещение “, 1982 г.

6. Мукусиев Б. А. Использование аналогии при решении физических задач.

//Физика в школе// №6, 1991 г.

7. Мякишев Г. Я., Буховцев Б. Б. Физика 11: учебник для 11 класса средней школы. М. “ Просвещение “, 1991 г.

8. Мякишев Г. Я., Буховцев Б. Б. Физика 10: учебник для 10 класса средней школы. М. “ Просвещение “, 1990 г.

9. Родина Н. А. Световые явления . М. “ Просвещение “, 1986 г.

10. Физика 11: учебное пособие для 11 класса школ и классов с углубленным изучение физики, под редакцией Пинского А. А. М. “ Просвещение “, 1995 г.