Навигация
1. Функция Лобачевского.
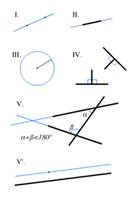
Как уже говорилось выше, через т. С в плоскости САВ проходят 2 направленные параллели к прямой АВ (СЕ и CF), симметрично расположенные относительно перпендикуляра CD (рис.5). Угол параллельности, образованный каждой из этих параллелей с CD, является острым, его величина не постоянна и зависит от расстояния CD(в геометрии Евклида угол параллельности всегда прямой). То, что угол параллельности острый, вытекает непосредственно из аксиомы Лобачевского. В изменении этого угла с изменением расстояния CD можно убедиться путем следующих рассуждений (рис.6).
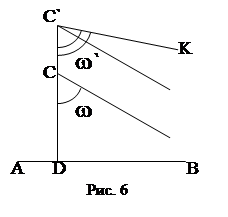 Пусть C’D>CD, CE || AB, в т. С угол параллельности – W. Пусть далее прямая C’E ‘|| AB в т. С’ угол параллельности - W’. В силу свойства транзитивности CE ||C’E’. Ясно, что W¹W’. Действительно, если допустить, что W= W’, то следует также допустить, что C’E’ и CE – расходящиеся прямые, как было показано выше, а это неверно.
Пусть C’D>CD, CE || AB, в т. С угол параллельности – W. Пусть далее прямая C’E ‘|| AB в т. С’ угол параллельности - W’. В силу свойства транзитивности CE ||C’E’. Ясно, что W¹W’. Действительно, если допустить, что W= W’, то следует также допустить, что C’E’ и CE – расходящиеся прямые, как было показано выше, а это неверно.
Построим C’K, образующую с CD угол a= w, ясно, что w’< a , т.к. параллельC’E’ ближе к перпендикуляру, чем расходящаяся C’K. Итак, w' < w ; отсюда следует, что угол параллельности убывает по мере удаления от прямой АВ; чем ближе т. С к прямой АВ, т.е. чем короче перпендикуляр CD, тем больше угол параллельности. Если обозначить расстояние т. С от прямой АВ, т.е. длину перпендикуляра CD через х, то можно сказать, что угол параллельности есть функция от х, названная «функцией Лобачевского» и обозначаемая П (х). Это монотонно убывающая функция. При изменении аргумента х от 0 до ¥ функция П (х) непрерывно изменяется соответственно от p /2 до 0. Таким образом ,![]() ,
, ![]()
При х ® 0 , иными словами, если оставаться в пределах сравнительно небольших расстояний, то угол параллельности мало отличается от p /2 то есть от этого значения, которое он имеет в евклидовой геометрии, это означает, что геометрия Лобачевского не противоречит, не исключает геометрии Евклида; последнего можно рассматривать как частный случай большой общей геометрии – геометрии Лобачевского. Реальный смысл предельного перехода (при х ® 0) от геометрии Лобачевского к геометрии Евклида состоит в том, что физика изучает, в конечном счете, только ограниченную, сравнительно небольшую часть пространства. Вот почему в окружающей нас среде (даже в пределах нашей планеты) свойства физического пространства приблизительно таковы, какими мы их знаем из Евклидовой геометрии, но для всего пространства, для мира звезд, для вселенной в целом, они иные, неевклидовы.
2. Сумма углов треугольника меньше 2d.
 Это предположение эквивалентно аксиоме Лобачевского, то есть из него вытекает эта аксиома и наоборот. Для примера докажем первое. Пусть ( рис.7) в прямоугольном треугольнике CDK сумма углов S= a+b+g<2d, то есть b+g<d .Это значит, что внутри угла NCK можно построить ÐLCK = а (NC^CD).
Это предположение эквивалентно аксиоме Лобачевского, то есть из него вытекает эта аксиома и наоборот. Для примера докажем первое. Пусть ( рис.7) в прямоугольном треугольнике CDK сумма углов S= a+b+g<2d, то есть b+g<d .Это значит, что внутри угла NCK можно построить ÐLCK = а (NC^CD).
Прямая CL не может пересечь прямой АВ в какой- либо точке М, так как если бы это случилось, то угол DKC , внешний по отношению к треугольнику KCM , равнялся бы внутреннему, не смежному с ним углу треугольника KCM, что противоречит абсолютной геометрии о внешнем угле треугольника. Итак, через т. С, кроме CN , проходит еще одна прямая – CL, не встречающая прямой АВ ; следовательно, верна аксиома Лобачевского. Разность 2d – S, то есть между 2d и суммой углов данного треугольника, называется угловым дефектом этого треугольника.
3. Предложение «сумма углов четырехугольника меньше 4d» вытекает из предыдущего. Отсюда следует, что в геометрии Лобачевского нет ни прямоугольников, ни квадратов. Вообще сумма углов n – угольника меньше 2d(n-2).
4. Внешний угол треугольника больше суммы внутренних, с ним не смежных углов. Действительно, пусть d - внешний угол треугольника, смежный с внутренним углом треугольника a , и пусть b и g - остальные его внутренние углы, тогда: a + d = 2d.
Следует, что d > b + g .
5. Если три угла одного треугольника соответственно равны трем углам другого треугольника, то эти треугольники равны между собой. Это четвертый признак равенства треугольников в геометрии Лобачевского.
Таким образом, в плоскости Лобачевского треугольник вполне определяется своими углами. Стороны и углы зависят друг от друга. Отсюда ясно, что в геометрии Лобачевского нет подобных фигур. Действительно, ведь из существования подобных фигур вытекает евклидова аксиома параллельности (доказательство Валлиса).
6. Площади. Уже известно, что, чем меньше размеры фигур, которые мы изучаем, тем ближе к геометрии Евклида, в которой угловой дефект треугольника равен 0. Доказывается следующая теорема: площадь треугольника прямопропорциональна его угловому дефекту. Чем меньше размеры фигуры, тем меньше ее дефект, тем меньше площадь. Однако угловой дефект по определениям не может превзойти 2d, следовательно, и площадь треугольника в геометрии Лобачевского не может стать больше некоторой, определенной, конечной величины.
Таковы некоторые из основных идей и фактов геометрии Лобачевского. После работы «О началах геометрии», появились в свет и другие произведения Лобачевского по неевклидовой геометрии: «Воображаемая геометрия» (1835), «Применение воображаемой геометрии к некоторым интегралам» (1836), «Новые начала геометрии с полной теорией параллельных», опубликованные в «Ученых записках Казанского университета» в 1835-1838г.г., «Геометрические исследования по теории параллельных» (опубликованы впервые в1840г. в Берлине на немецком языке). Однако идеи Лобачевского были настолько революционными и до того опередили свой век, что не могли быть понятыми даже крупными математиками того времени. Поэтому новая геометрия не была признана современниками, была встречена с полным равнодушием и даже с иронией. Ее многие считали сплошной фантазией, а ее автора чудаком или даже невеждой. Одинокий Лобачевский не отказался от своих идей. Он твердо был убежден в логической правильности неевклидовой геометрии. Чтобы можно было это доказать, Лобачевский предпринимал астрологические наблюдения, и производил измерения углов космических треугольников, стороны которых измерялись расстояниями от Земли до небесных тел, в надежде установить, равна ли сумма углов треугольника 2dили она меньше двух прямых углов. Однако, измерения не могли дать определенного результата в силу их приближенного характера. Лобачевский всю жизнь искал оправдания своей геометрии в механике и астрономии и не переставал верить, что торжество его идей неминуемо.
В 1855г. умирает Гаусс, единственный крупный ученый, сумевший оценить Лобачевского по достоинству при его жизни, хотя и не решившись выступить публично в защиту новой геометрии. В этом же году, Лобачевский, которого постоянное умственное напряжение и тяжелые переживания, перенесенные в борьбе за признание своих идей, довели до потери зрения, диктует последнее свое произведение «Пангеометрия»*. Лобачевский умер в 1856 г. непризнанным, почти забытым.
Не получил признание при жизни и гениальный венгерский математик Янош Бояй (1802-1860). Его «Appendix», содержащий основы неевклидовой геометрии, изложен исключительно сжато и схематично – вот одна из причин, сделавших это классическое произведение недоступным для его современников.
города Марош-Варигархен. За это время он опубликовал здесь некоторые свои работы, в том числе и теорему о равновеликости и равносоставленности многоугольников, включив ее в важнейший свой труд «Temtamen» («Опыт»), более полное заглавие, гласит в русском переводе: «Опыт введения юных учащихся в начала чистой математики, элементарной и высшей» (1832). В виде приложения именно к этому труду и был опубликован «Appendix» Яноша Бояй.
--------------------------------
*Греческое слово «пан» в сложных словах означает «все», «Пангеометрия» - «Всеобщая геометрия»
После того, как стало известно, что Гаусс считал геометрию Лобачевского логически вполне правильной, «неевклидова геометрия»(названная так именно Гауссом), привлекла к себе внимание многих математиков. Произведения Лобачевского и «Appendix» Бояй были переведены на французский, итальянский и другие языки. Однако, выявилось много противников неевклидовой геометрии, которые отнеслись к ней с недоверием, утверждая, что она представляет собой сплошную фантазию, нелепость, которая рано или поздно будет обнаружена. Положение коренным образом изменилось, когда итальянский математик, профессор римского университета Эудженио Бельтрами (1835-1900) нашел модель для неевклидовой геометрии, показав в своей работе «Опыт интерпретации неевклидовой геометрии»(1868г.), что наряду с плоскостями, на которых осуществляется евклидова геометрия, и сферическими поверхностями, на которые действуют формулы сферической геометрии, существуют и такие реальные поверхности, названные им псевдосферами (рис.8), на которых частично осуществляется планиметрия Лобачевского.
 Известно, что сферу можно получить вращением полуокружности вокруг своего диаметра. Подобно тому, псевдосфера образуется вращением линии FCE, называемой трактрисой, вокруг ее оси АВ (рис.9).Итак, псевдосфера – это поверхность в обыкновенном реальном пространстве, на котором выполняются многие аксиомы и теоремы неевклидовой планиметрии Лобачевского. Например, если начертить на псевдосфере треугольник, то легко усмотреть, что сумма его внутренних углов меньше 2d. Сторона треугольника – это дуги псевдосферы, дающие кратчайшее расстояние между двумя ее точками и выполняющие ту же роль, которую выполняют прямые на плоскости. Эти линии, называемые геодезическими, можно получить, зажав туго натянутую и политую краской или мелом нить, в вершинах треугольника. Таким образом, для планиметрии Лобачевского была найдена реальная модель - псевдосфера. Формулы новой геометрии Лобачевского нашли конкретное истолкование. Ими можно было пользоваться, например, для решения псевдосферических треугольников.
Известно, что сферу можно получить вращением полуокружности вокруг своего диаметра. Подобно тому, псевдосфера образуется вращением линии FCE, называемой трактрисой, вокруг ее оси АВ (рис.9).Итак, псевдосфера – это поверхность в обыкновенном реальном пространстве, на котором выполняются многие аксиомы и теоремы неевклидовой планиметрии Лобачевского. Например, если начертить на псевдосфере треугольник, то легко усмотреть, что сумма его внутренних углов меньше 2d. Сторона треугольника – это дуги псевдосферы, дающие кратчайшее расстояние между двумя ее точками и выполняющие ту же роль, которую выполняют прямые на плоскости. Эти линии, называемые геодезическими, можно получить, зажав туго натянутую и политую краской или мелом нить, в вершинах треугольника. Таким образом, для планиметрии Лобачевского была найдена реальная модель - псевдосфера. Формулы новой геометрии Лобачевского нашли конкретное истолкование. Ими можно было пользоваться, например, для решения псевдосферических треугольников.
Псевдосферу, которую мы назвали «моделью», Бельтрами назвал интерпретацией (истолкованием) неевклидовой геометрии на плоскости. Впоследствии, с развитием и введением в математику аксиоматического метода, под интерпретацией (или моделью) некоторой системы аксиом стали понимать любое множество объектов, в которых данная система аксиом находит свое реальное воплощение, то есть, любая совокупность объектов, отношение между которыми полностью совпадают с теми, которые описываются в данной системе аксиом. При этом полагают, что если для некоторой системы аксиом существует или можно построить интерпретацию (модель), то эта система аксиом непротиворечива, то есть, не только сами аксиомы, но и любые теоремы, на них логически основывающиеся никогда не могут противоречить одна другой.
Итак, доказательство логической непротиворечивости той или иной геометрии, можно свести к доказательству существования модели соответствующей системы аксиом.
Первой моделью планиметрии Лобачевского была интерпретация Бельтрами в 1868г., к которой позже, но из других соображений и в ином виде, пришел в 1870г. немецкий математик Феликс Клейн. Идею этой интерпретации можно усмотреть в приведенном выше рис.4. В качестве плоскости Лобачевского, коротко «плоскость L», принимается внутренность некоторого круга (исключается таким образом его контур) на обычной евклидовой плоскости. Прямыми L служат хорды круга, исключая, конечно, их концы. Принадлежность и между понимаются в обычном евклидовом смысле. Оказывается, что в этой модели имеют место все аксиомы абсолютной геометрии, то есть, аксиомы принадлежности, порядка, конгруэнтности, непрерывности. Что же касается аксиомы параллельности, то в этой модели имеет место не постулат Евклида, а именно, аксиома Лобачевского: через т. С, не лежащую на данной прямой (хорде) АВ, можно провести хотя бы 2 прямые (хорды), не пересекающие данную. Выполняются, конечно, так же все следствия аксиомы. Так, например, среди проходящих через данную точку расходящихся прямых L, имеются две предельные CL и CM, параллельные к АВ в смысле Лобачевского, так как разделяют класс расходящихся с АВ прямых от класса сходящихся. Сами параллельные не имеют с АВЫ общих точек, поскольку точки А и В, лежащие на окружности, исключены.
Аналогично строится модель Клейна геометрии Лобачевского в пространстве, принимая внутренность какого-либо шара за пространство L.
Таким образом, была показана непротиворечивость геометрии Лобачевского. Ее аксиомы и теоремы не могут быть противоречивыми, так как каждой из них соответствует факт евклидовой геометрии внутри круга (или внутри шара). Если в геометрии Лобачевского встретились бы две противоречащие друг другу теоремы, то, переводя эти теоремы на язык обычной геометрии посредством модели Клейна, мы получили бы противоречие между соответствующими теоремами в геометрии Евклида, то есть, построением модели, Клейн показал, что геометрия Лобачевского непротиворечива в такой же мере, в какой непротиворечива геометрия Евклида.
Другую модель геометрии Лобачевского построил в 1882г. французский математик Анри Пуанкаре (1854-1912), применивший ее к решению некоторых важных задач теории функций комплексного переменного.
Одним из важнейших результатов открытия геометрии Лобачевского (называемой также гиперболической геометрией) было развитие новых неевклидовых геометрий, в первую очередь, геометрии Римана (в узком смысле), называемой так же эллиптической геометрией. В качестве модели планиметрии Римана может служить сфера, если считать каждую пару диаметрально противоположных ее точек за одну «точку».
Итак, плоскость Римана представлена Евклидовой сферой. На сфере нет прямых линий, но имеются так называемые большие окружности (рис.10), то есть окружности с центром в в центре сферы, которые в качестве геодезических ее линий выполняют на сфере ту же роль, что и прямые на плоскости. Дуги больших окружностей дают кратчайшие расстояния между двумя точками сферы, через которые они проходят, подобно тому, как отрезок прямой на плоскости представляет кратчайшее расстояние между двумя точками сферы, через которую они проходят, подобно тому, как отрезок прямой на плоскости представляет кратчайшее расстояние между его концами; через две точки сферы проходит одна и только одна большая окружность, подобно тому, как две точки плоскости определяют одну и только одну прямую; из дуг больших окружностей на сфере, как из отрезков прямых на плоскости можно образовать сферические треугольники, четырехугольники, многоугольники. Одним словом, большие окружности сферы – это ее «прямые» (рис.11). Однако, наряду с некоторыми сходствами, имеется и большое различие между сферической геометрией с одной стороны и геометрией Евклида и Лобачевского с другой. Аксиомы, следовательно, и теоремы, и формулы сферической геометрии во многом отличаются от аксиом, теорем и формул плоской геометрии Евклида, а так же Лобачевского. В частности, прямые Римана все замкнуты и конечны, имея одну и ту же длину. Сумма углов сферического треугольника, как известно, больше 2d, каждые две прямые имеют одну общую точку, то есть, на римановой плоскости нет параллельных прямых.
В разработку эллиптической геометрии значительный вклад внес Гаусс своими исследованиями о поверхностях.
Сравнивая три, в известном смысле дополняющих друг друга , геометрии: гиперболическую, евклидову (называемую так же параболической) и эллиптическую, следует отметить, что в первой из них через точку вне данной прямой можно провести к этой прямой две параллельные, во второй – одну, а в третей – ни одной. В первой сумма внутренних углов треугольника меньше 2d, во второй равна 2d, а в третей – меньше 2d.
Возникшие из попыток доказательства V постулата неевклидовы геометрии, открытые Лобачевским, Бояй, Гауссом и Риманом и развитые в трудах Бельтрами, Кэли, Клейна, Пуанкаре и других ученых, стали в наши дни необходимым аппаратом для изучения механики, физики и астрономии. Особенно важна геометрия Лобачевского для теории относительности, так как группа важных для теории относительности «преобразований Лоренца» изоморфна группе движений пространства Лобачевского. С другой стороны, открытие неевклидовой геометрии привело к новым исследованиям в области оснований геометрии и, в частности, к аксиоматике Гильберта. Отказываясь от аксиомы Архимеда или от аксиомы Кантора, он получает «неархимедову» соответственно «неканторову» геометрию и т.п.
Открытие неевклидовой геометрии, начало которому положил Лобачевский, не только сыграло огромную роль в развитии новых идей и методов в математике естествознании, но имеет и философское значение. Господствовавшее до Лобачевского мнение о незыблемости геометрии Евклида в значительной мере основывалось на учении известного немецкого философа И. Канта (1724-1804), родоначальника немецкого классического идеализма. Кант утверждал, что человек упорядочивает явления реального мира согласно априорным представлениям, а геометрические представления и идеи якобы априорны (латинское слово aprior означает – изначально, заранее), то есть, не отражают явлений действительного мира, не зависят от практики, от опыта, а являются врожденными человеческому миру, раз и навсегда зафиксированными, свойственными человеческому разуму, его духу. Поэтому , Кант считал, что Евклидова геометрия непоколебима, неизменна, и является вечной истиной. Еще до Канта геометрия Евклида считалась незыблемой, как единственно возможное учение о реальном пространстве.
Открытие неевклидовой геометрии доказало, что нельзя абсолютировать представления о пространстве, что «употребительная» (как назвал Лобачевский геометрию Евклида) геометрия не является единственно возможной, однако это не подорвало незыблемость геометрии Евклида. Итак, в основе геометрии Евклида лежат не априорные, врожденные уму понятия и аксиомы, а такие понятия, которые связаны с деятельностью человека, с человеческой практикой. Только практика может решить вопрос о том, какая геометрия вернее излагает свойства физического пространства. Открытие неевклидовой геометрии дало решающий толчок грандиозному развитию науки, способствовало и поныне способствует более глубокому пониманию окружающего нас материального мира.
Библиография
1. Г.И. Глейзер. История математики в школе IX – X классы. Пособие для учителей. Москва, «Просвещение» 1983г.
2. Даан Дальмедино А., Пейффер И. Пути и лабиринты. Очерки по истории математики. Перевод с французского. М: Мир.1986г.
3. Б.Л. Лаптев. Н.И. Лобачевский и его геометрия. Пособие для учащихся. М. «Просвещение», 1970г.
4. И.М. Яглам. Принцип относительности Галилея и неевклидова геометрия.Серия «Библиотека математического кружка» М: 1963г.
Приложение 1Николай Иванович Лобачевский, второй сын мелкого чиновника, родился 1 декабря(20 ноября) 1792 года в Нижнем Новгороде, в России. Когда Николаю было 7 лет, его мать, Прасковья Ивановна, осталась одна с тремя маленькими сыновьями. И до этого жалование отца с трудом хватало на содержание семьи; теперь она встретилась с крайней нищетой. Она переехала в Казань, где как могла, подготавливала детей к школе, и они были приняты в гимназию на казенное содержание. Николай приступил к занятиям в 1802 году, в десятилетнем возрасте. Его успехи в математике и в древних языках были феноменальными. В 14 лет он был подготовлен для университета. В 1807 году он поступил в Казанский университет, в котором ему предстояло провести последующие 40 лет жизни – как студенту, экстраординарному профессору, профессору и, наконец, ректору.
В 1811 году, в возрасте 18 лет, Лобачевский получил степень магистра, к тому же с отличием. В это же время его старший брат Алексей вел курсы элементарной математики по подготовке младших правительственных чиновников, и, когда он получил отпуск по болезни, Николай заменил его. В апреле1814 года он был утвержден адъюнктом чистой математики, а 2 года спустя ему было присвоено звание профессора.
Назначение Лобачевского экстраординарным профессором состоялось в 1816 году в необычно молодом возрасте 23 лет. Его обязанности были многотрудными. Дополнительно к работе по математике ему поручались лекционные курсы по астрономии и физике. Он блестяще справился с порученным заданием. Это послужило поводом для еще большей нагрузки.
Вскоре Лобачевский взялся за переустройство университетской библиотеки и университетского музея, находившихся в хаотическом состоянии.
Со смертью Александра I дела обернулись к лучшему. Специальный уполномоченный правительства для преднамеренного преследования Казанского был уволен. Нуждаясь в политической и моральной поддержке своей деятельности в университете, новый попечитель обеспечил назначение в 1827 году Лобачевского ректором. Математик был теперь главой университета, но эта должность отнюдь не была синекурой. Под его умелым руководством весь штат был реорганизован, были привлечены лучшие люди, преподавание было либерализовано, несмотря на официальные препятствия, была построена библиотека, соответствующая высшему уровню научных требований, были организованы механические мастерские для изготовления научных инструментов, которые требовались для исследований и преподавания, была основана и оборудована обсерватория – любимое детище энергичного ректора.
Даже ректорское достоинство не удерживало Лобачевского от работы руками в библиотеке и музее, когда он чувствовал, что его помощь необходима. Университет был его жизнью, и он любил его.
Кажется невероятным, что Лобачевский, так сильно перегруженный преподавательскими и административными обязанностями, мог находить время для научной работы. Он создал один из величайших шедевров всей математики – неевклидову геометрию и поставил веху в человеческом мышлении. Он трудился над этим с перерывами не менее 20 лет. Его первое публичное сообщение по этой теме было сделано на физико – математическом факультете Казанского университета в 1826 году.
В 1846 году его грубо лишили должностей профессора и ректора университета, хотя тогда он был полон физических и умственных сил, более чем когда- либо он был способен продолжать свои математические исследования. Отвратительная неблагодарность властей сломила Лобачевского. Он оставил все надежды снова стать кем-то в университете, который своей научной славой почти целиком был обязан его усилиям, и после этого появлялся в нем только случайно, чтобы помочь на экзаменах. Хотя его зрение быстро ухудшалось, он был еще способен к интенсивному математическому мышлению.
Он все еще любил университет. Его здоровье пошатнулось, когда умер его сын; но он все еще надеялся, что сможет принести некоторую пользу. В 1855 году университет праздновал свое пятидесятилетие. Лобачевский лично присутствовал на торжествах и принес в дар юбиляру экземпляр «Пангеометрии» – завершающей научной работы его жизни. Эта работа не была написана его собственной рукой: он диктовал ее, так как в то время был уже слепым. Через несколько месяцев, 24 февраля 1856 года, 62-х лет от роду, он умер.
Приложение 2Жизнь и творчество Яноша Бояй тесно связаны с деятельностью его отца, математика Фаркаша Бояй (1775-1856). Большую часть своей жизни отец и сын провели в родной Трансильвании. Еще будучи студентом Геттингенского университета, Бояй-отец дружил с юным Гауссом, в беседах с которым он часто обсуждал проблему V постулата. Впоследствии Ф. Бояй много лет занимается исследованиями в области теории параллельных линий, которые, однако, не привели его к желаемому результату. С 1804г. и почти до конца своей жизни он работал в должности преподавателя математики, физики и химии в евангелистско-реформистской коллегии небольшого трансильванского
Одаренность Яноша и его страстный интерес к математике и музыке складывались еще в детстве. В
.возрасте 10 лет он уже имел свои собственные музыкальные композиции, в 13 лет владел дифференциальным и интегральным исчисленьями, а в 15 лет – выдержал экзамен на аттестат зрелости. В 1818г. Янош отправился в Вену , где на протяжении 4 лет состоял студентом военно-инженерной академии. В 1823г., окончив академию и получив звание офицера, Янош был отправлен на службу в трансильванский город Темешвар Здесь, располагая достаточным временем, он всецело отдался математике и со страстным увлечением занялся исследованием проблемы V постулата, начатым еще в годы студенчества. В одном из своих писем, направленных в 1823г. отцу, Янош сообщил, что хотя и не достиг еще цели, но получил значительные результаты: "Из ничего я создал новый мир"
Отец, на собственном опыте узнавший, сколько горя и разочарований может принести проблема V постулата, в своих письмах умолял сына отказаться от этих занятий. Однако, Янош продолжал свои исследования, добился цели и, тщательно отработав свои исследования, убедил почти ничего не понявшего в них отца, поместить их в качестве «Приложения» в конце «Тентамена». Работа была послана отцом на отзыв Гауссу. Последний, однако, вместо одобрения молодого венгерского математика , в ответном письме писал, что содержание этой работы и ее результаты почти сплошь совпадения с его, которые он получил уже30-35 лет тому назад.
Ответ Гаусса произвел на Яноша Бояй удручающее впечатление. Не зная о том, что приоритет открытия неевклидовой геометрии принадлежал уже с 1829г. Н.И. Лобачевскому, он не поверил, что Гаусс пришел к тем же идеям независимо от него, Яноша Бояй. Он заподозрил Гаусса в намерении похитить у него приоритет великого открытия, ставшего для Яноша делом и смыслом всей его жизни.
Его переживания и отчаяние резко возросли, когда в его руки попало сочинение Н.И. Лобачевского на немецком языке «Геометрические исследования по теории параллельных линий». Янош высказал предположение , что Лобачевский – это всего лишь псевдоним, под которым скрывается Гаусс, похитивший у него приоритет открытия неевклидовой геометрии.
Когда в 60-х годах прошлого столетия была опубликована переписка Гаусса с его друзьями, ученые узнали, что Гаусс полностью разделял взгляды Лобачевского и Бояй, и сам, независимо от них, пришел к тем же идеям.
Приложение 3
Карл Фридрих Гаусс родился 30 апреля 1777 года в доме №1550, что стоял на канале Венденгребене в Брауншвейе. По мнению биографов, он унаследовал от родных отца крепкое здоровье, а от родных матери яркий интеллект. Ближе других был к будущему ученому дядя Фридерихс – искусный ткач, в котором, по словам племянника, «погиб прирожденный гений».Гаусс говорил о себе, что он «умел считать, раньше, чем говорить». Самая ранняя математическая легенда о нем утверждает, что в 3 года он следил за расчетами отца с каменщиками -–поденщиками и неожиданно поправил отца, причем оказался прав.
В 7 лет Карл Фридрих поступил в Екатериненскую народную школу. Поскольку считать там начинали с третьего класса, первые два года на маленького Гаусса внимания не обращали. В 3-й класс ученики обычно попадали в 10-летнем возрасте и учились там до конфирмации (15 лет). Учителю Бюттнеру приходилось заниматься одновременно с детьми разного возраста и разной подготовки. Поэтому он давал обычно части учеников длинные задания на вычисление, с тем, чтобы иметь возможность беседовать с другими учениками. Однажды группе учеников, среди которых был Гаусс, было предложено просуммировать натуральные числа от 1 до100. По мере выполнения задания ученики должны были класть на стол учителя свои грифельные доски. Порядок досок учитывался при выставлении оценок. 10-и летний Гаусс положил свою доску, едва Бюттнер кончил диктовать задание. К всеобщему удивлению, лишь у него ответ был правилен. Секрет был прост: Пока диктовалось задание Гаусс успел переоткрыть формулу для суммы арифметической прогрессии! Слава о чудо-ребенке распространилась по маленькому Брауншвейгу.
В школе, где учился Гаусс, помощником учителя, основной обязанностью которого было чинить перья младшим ученикам работал некто Бартельс, интересовавшийся математикой и имевший несколько математических книг. Гаусс и Бартельс начинают заниматься вместе; они знакомятся с биномом Ньютона, бесконечными рядами…..
Через некоторое время Бартельс получит кафедру чистой математики в Казанском университете и будет учить математику Лобачевского.
О Гауссе узнают при дворе. В1791 году его представляют Карлу Вильгельму Фердинанду – герцогу Брауншвейгскому. Мальчик бывает во дворце и развлекает придворных искусством счета. Благодаря покровительству герцога Гаусс смог в октябре 1795 года поступить в Геттингенский университет. Первое время он слушает лекции по филологии и почти не посещает лекции по математике. Но это не означает, что он не занимается математикой.
Феликс Клейн, замечательный математик, глубокий исследователь научного творчества Гаусса, говорил о великом ученом следующее: «Естественный интерес, детское любопытство приводит впервые мальчика независимо от каких-либо внешних влияний к математическим вопросам. Первое, что его привлекает, это чистое искусство счета. Он беспрестанно считает с прямо-таки непреоборимым упорством и неутомимым прилежанием. Благодаря этим постоянным упражнениям в действиях над числами, например, над десятичными дробями с невероятным числом знаков, он не только достигает изумительной виртуозности в технике счета, которой он отличался всю свою жизнь, но его память овладевает таким колоссальным числовым материалом, он приобретает такой богатый опыт и такую широту кругозора в области чисел, какими навряд ли обладал кто-либо до или после него. Осенью 1795 года Гаусс переезжает в Геттинген и прямо-таки проглатывает впервые попавшуюся в его руки литературу: Эйлера и Лагранжа».
«Рассказывают, что Архимед завещал построить над своей могилой памятник в виде шара и цилиндра в память о том, что он нашел отношение объемов цилиндра и вписанного в него шара 3:2. Подобно Архимеду Гаусс выразил желание, чтобы в памятнике на его могиле был увековечен семнадцатиугольник. Это показывает, какое значение сам Гаусс придавал своему открытию. На могильном камне Гаусса этого рисунка нет, но памятник, воздвигнутый ему в Брауншвейге, стоит на семнадцатиугольном постаменте, правда, едва заметном зрителю». (Г. Вебер)
Похожие работы
... представить другие геометрии Кант счел достаточным основанием, чтобы утверждать, что другие геометрии не могут существовать. Появление неевклидовой геометрии Но многовековые попытки доказательства пятого постулата Евклида привели в конце концов к появлению новой геометрии, отличающейся от евклидовой тем, что в ней V постулат не выполняется. Эта геометрия теперь называется неевклидовой, а в ...
... , т. е. такие пары точек считаются за одну точку. Из этого определения следует, что при возрастании n число типов неевклидовых пространств также растет. Неевклидовы геометрии являются геометриями простейших римановых пространств определенной и неопределенной метрики, составляющих так называемый класс пространств постоянной ненулевой кривизны. Каждое из таких n-мерных пространств допускает ...
... целых три доказательства V постулата, ошибочность которых быстро показали его современники. Последнее «доказательство» он опубликовал в 1823 году, за три года до первого доклада Лобачевского о новой геометрии. Открытие неевклидовой геометрии В первой половине XIX века по пути, проложенному Саккери, пошли сразу три математика: К.Ф. Гаусс, Н.И. Лобачевский и Я. Бойяи. Но цель у них была уже иная ...
... живой. Пусть новых линий не начертят руки, Он здесь стоит, взнесенный высоко, Как утверждение бессмертья своего, Как вечный символ торжества науки. Другие авторы. Идея неевклидовой геометрии пришла в голову не только Лобачевскому – просто ему относительно повезло. Одним из «конкурентов» был Гаусс – великий затворник, отказавшийся от услуг почты, чтобы никто не смог обвинить его в плагиате. ...


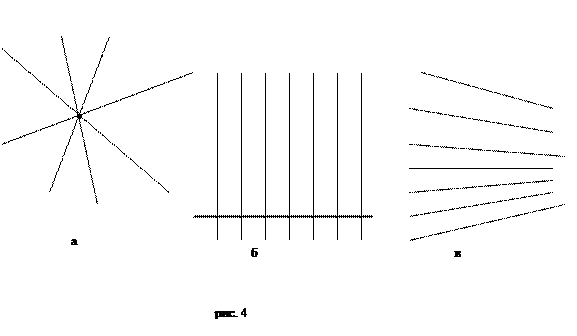
0 комментариев