Навигация
Специфика развития математических способностей детей олигофренов
2. Специфика развития математических способностей детей олигофренов
В связи с проблемой формирования и развития способностей следует указать, что целый ряд исследований психологов направлен на выявление структуры способностей школьников к различным видам деятельности. При этом под способностями понимается комплекс индивидуально - психологических особенностей человека, отвечающих требованиям данной деятельности и являющиеся условием успешного выполнения. Таким образом, способности – сложное, интегральное , психическое образование, своеобразный синтез свойств, или, как их называют компонентов.
Общий закон образования способностей состоит в том, что они формируются в процессе овладения и выполнения тех видов деятельности, для которых они необходимы.
Способности не есть нечто раз и навсегда предопределённое, они формируются и развиваются в процессе обучения, в процессе упражнения, овладения соответствующей деятельностью, поэтому нужно формировать , развивать, воспитывать, совершенствовать способности детей и нельзя заранее точно предвидеть как далеко может пойти это развитие.
Говоря о математических способностях как особенностях умственной деятельности, следует прежде всего указать на несколько распространенных среди учителей заблуждений.
Во-первых, многие считают, что математические способности заключаются прежде всего в способности к быстрому и точному вычислению (в частности в уме). На самом деле вычислительные способности далеко не всегда связаны с формированием подлинно математических (творческих) способностей. Во-вторых, многие думают, что способные к математике школьники отличаются хорошей памятью на формулы, цифры, числа. Однако, как указывает академик А. Н. Колмогоров, успех в математике меньше всего основан на способности быстро и прочно запоминать большое количество фактов, цифр, формул. Наконец, считают, что одним из показателей математических способностей является быстрота мыслительных процессов. Особенно быстрый темп работы сам по себе не имеет отношения к математических способностям. Ученик может работать медленно и неторопливо, но в то же время вдумчиво, творчески, успешно продвигаясь в усвоении математики.
Крутецкий В.А. в книге «Психология математических способностей школьников» различает девять способностей (компонентов математических способностей):
1) Способность к формализации математического материала, к отделению формы от содержания, абстрагированию от конкретных количественных отношений и пространственных форм и оперированию формальными структурами, структурами отношений и связей;
2) Способность обобщать математический материал, вычленять главное, отвлекаясь от несущественного, видеть общее во внешне различном;
3) Способность к оперированию числовой и знаковой символикой;
4) Способность к «последовательному, правильно расчленённому логическому рассуждению», связанному с потребностью в доказательствах, обосновании, выводах;
5) Способность сокращать процесс рассуждения, мыслить свернутыми структурами;
6) Способность к обратимости мыслительного процесса (к переходу с прямого на обратный ход мысли);
7) Гибкость мышления, способность к переключению от одной умственной операции к другой, свобода от сковывающего влияния шаблонов и трафаретов;
8) Математическая память. Можно предположить, что её характерные особенности также вытекают из особенностей математической науки, что это память на обобщения, формализованные структуры, логические схемы;
9) Способность к пространственным представлениям, которая прямым образом связана с наличием такой отрасли математики как геометрия;
Рассматривая развитие математических способностей младших школьников в при помощи компонентов математических способностей Крутецкого В.А., можно сказать, что:
У детей младшего школьного возраста с нарушением интеллекта наблюдается более простой вид обобщений – движение от частного к известному общему, подвести частный случай под общее правило. Абстрагирование у этих детей выражено гораздо слабее, чем у их сверстников, которые учатся в простых классах. Большое влияние на их рассуждения оказывают несущественные признаки. Поэтому с такими детьми нужно работать тщательнее, усерднее.
Способность к оперированию числовой и знаковой символикой детям даётся нелегко, дети с большим трудом запоминают определения, формулировки, общие схемы рассуждений. Путаются в операциях «сложения» и «вычитания», не запоминают названия некоторых цифр.
Свернутость мышления в младшем школьном возрасте проявляется лишь в самой элементарной форме. Детям же классов коррекции это даётся ещё труднее.
Говоря о гибкости мыслительных процессов, можно сказать, что у данных детей она развита на самом низком уровне. Им очень трудно переключаться от одной умственной операции к другой, нужен отдых. Утомляемость этих детей повышена. Без наглядных пособий, шаблонов и трафаретов, которыми в основном пользуются учителя, детям труднее воспринимать материал.
Проявление математической памяти в её развитых формах не наблюдается. Дети запоминают цифры, операции с трудом. Математическая память находится на низком уровне.
Этим детям Аргинская И.И рекомендует использовать геометрические фигуры, их использование позволяет опираться на наглядные образы, выполнять предлагаемые задания в наглядно-действенном плане, что облегчает учащимся достижение успеха. Способность к пространственным представлениям у детей так же не развита как и перечисленные выше компоненты математических способностей.
Утомляемость детей к математике повышена. Поэтому уроки математики должны быть интересными, занимательными. Нужно учитывать индивидуальные особенности детей, проводить физкультминутки, чтобы снять утомление.
Глава 2. Методика формирования вычислительных навыков в специальных коррекционных школах
На изучение математики в учебном плане специальной школы отводится большая часть всего времени. Но математика является одним из предметов, который вызывает значительные затруднения у большого количества учащихся.
Одна из главных причин такого положения: подмена основной функции изучения математики – формирование математических понятий, установление связей между ними, с которыми встречаются дети как в школе так и вне её – выработкой вычислительных навыков.
Формирование вычислительных навыков – трудоемкое и порой скучная для учащихся работа, если не вноситься разнообразие в ее организацию. Один из приемов детей, следующий: в предлагаемых заданиях даны словесные формулировки познавательных вопросов, а также возможные варианты ответов, один из которых правильный. Учащиеся должны выбрать правильный ответ. Для этого им необходимо выполнить математические задания, например, вычисления.
Разнообразная подача математического материала эмоционально воздействует на детей. Дополнительные сведения познавательного характера способствуют активности учащихся, так как в заданиях подобным указанным выше:
1) Заложена смена деятельности детей (они слушают, думают, отвечают, составляют выражения, находят их значения и дописывают результаты);
2) Узнают интересные факты, что не только способствует взаимосвязи изучаемых в школе предметов, расширяет кругозор, способствует общему развитию, но и побуждает к самостоятельному познанию нового.
Опытный учитель знает, как важно, чтобы урок с самого начала «заладился». Если хорошо проведен устный счет, с известной долей уверенности можно сказать, что ребята будут активны. Задания подобранные с расчетом пробудить у учащихся интерес, сыграют свою роль - подготовят детей к восприятию нового материала, к решению предложенных упражнений.
При обучении в начальных классах наиболее распространена беседа. Это объясняется прежде всего психологическими особенностями детей, младшего школьного возраста. Вопрос стимулирует внимание детей, позволяет включать их в коллективную работу класса и осуществлять руководство познавательной деятельностью детей. -
Рассматривая метод как совокупность приемов деятельности учителя и учащихся, Ю. К. Бабанский пишет, что «метод беседы включает в себя приемы постановки вопросов в определенной логической последовательности, приемы постановки наводящих вопросов, приёмы активизации всех учеников в беседе, приемы коррекции ошибочных ответов, приемы формулирования выводов, обобщении, оценки деятельности учащихся»'. Такой подход наиболее эффективен в практике обучения, так как приемы, с одной стороны, конкретизируют особенности применения каждого метода на различных этапах обучения, с другой — расширяют возможности его использования.
Рассмотрим использование беседы на этапе устного счета. Прием постановки вопросов в определенной логической последовательности здесь не играет особой роли. Цель беседы на данном этапе — закрепить математические понятия, совершенствовать навыки устных вычислений. Вопросы обычно носят репродуктивный характер.
Приведем пример беседы, которая наиболее часто встречается в практике обучения.
Учитель предлагает:
1. Найди сумму чисел 80 и 7.
2. Увеличь 53 на 4.
3. К какому числу надо прибавить 20, чтобы получить 28?
4. Чему равна сумма чисел 25 и 14? Чему равна разность этих чисел?
Если учитель ограничивается продумыванием только содержания предлагаемых вопросов, то активность учащихся, как показывает практика, снижается. Поэтому на этапе устного счета учитель уделяет особое внимание приемам, активизирующим деятельность учащихся.
Перечислим эти приемы.
1. Использование демонстрационных карточек,
Учитель показывает две карточки с числами
8 и 7 и спрашивает, какие, действия можно выполнить с данными числами? (Сложение и вычитание.) Затем предлагает задания:
Найди сумму этих чисел.
Найди разность этих чисел.
Увеличь число 80 на 2, на 20.
Уменьши число 80 на 2, на 20.
После этого учитель выставляет на доске три карточки с числами 20, 9 и 11 и спрашивает:
— Какое число из данных трех чисел может быть уменьшаемым? Составь пример. Реши его устно. Какие числа из данных трех чисел могут быть слагаемыми? Составь примеры. Реши их устно.
2. Работа с перфокартами.
Каждый ученик получает индивидуальную перфокарту, содержащую одинаковые примеры с различными заданиями. Учащиеся выполняют задания самостоятельно.
№1 №2
75+ð=79 ð+4=79
90-ð=81 ð-9=81
54+ð=62 ð+8=82
48+ð=39 ð-9=39
№3 №4
75 4=79 75+4=ð
90 9=81 90-9=ð
54 8=62 54+8=ð
48 9=39 48-9=ð
После выполнения задания учитель проводит беседу.
— Прочитайте примеры, в которых находили разность. Прочитайте примеры, в которых находили сумму. К какому результату надо прибавить 9, чтобы получить 90? К какому результату надо прибавить 8, чтобы получить 70?
В данном случае метод беседы сочетается с методом самостоятельной работы учащихся. Такое сочетание в практике необходимо, а использование перфокарт активизирует учащихся в процессе беседы.
3. Запись выражений на доске.
3*8 4*4
6*5 3*10
8*2 6*4
Учитель предлагает задания.
— Увеличь первое произведение на 7. Уменьши второе произведение на 4. Найди разность второго и третьего выражений. Найди сумму пятого и шестого выражений. Прочитай выражения с одинаковыми значениями.
4. Использование индивидуальных карточек с числами.
У каждого ученика на парте лежат карточки с числами:
0 1 2 3 4 5 6 7 8 9
.Учитель читает выражение, например три умножить на восемь, ученики поднимают карточку с соответствующим числом (ответ).
3*8 (24)
6*5 (30)
8*2 (16)
5. Выбор ответов.
На доске выписаны числа:
32 34 53 84 41 78 96
Учитель читает выражения, учащиеся должны выбрать и прочитать соответствующее этому выражению значение:
4*8 (32)
35 + 6 (41)
80-2 (78)
6. Использование сигнальных карточек.
Учитель предлагает учащимся вопросы, связанные с нахождением значений выражений. Прочитав выражение, он показывает на одно из чисел, записанных на доске. Если ответ совпадает с указанным числом, ученик показывает зеленую карточку, если не совпадает — красную.
Например, на доске записаны числа:
23 43 35 48 14 87 69
Учитель предлагает увеличить на 4 число 39 и показывает на число 43. Ученик поднимает зеленую карточку. Далее учитель просит уменьшить на 5 число 29 и показывает на число 23. Ученик поднимает красную карточку. Учитель спрашивает, что ответ больше или меньше числа 23? На сколько больше? На сколько нужно уменьшить 29, чтобы получить 23?
Похожие работы
... ли Вы социальной политикой государства в отношении работников бюджетной сферы?» Анализ распределения ответов показал, что более ¾ работников специализированной коррекционной школы-интерната не удовлетворены социальной политикой государства в отношении работников бюджетной сферы. Только 7,5% респондентов ответили утвердительно на вопрос анкеты. 2.3 Основные выводы и рекомендации по ...
... . Нужно учитывать индивидуальные особенности детей, проводить физкультминутки, чтобы снять утомление. Глава 2. Методика развития математических способностей младших школьников в классах коррекции. 1.Особенности структурирования математического материала в классах коррекции. На изучение математики в учебном плане начальной школы отводится четвёртая часть всего времени. Также, ...
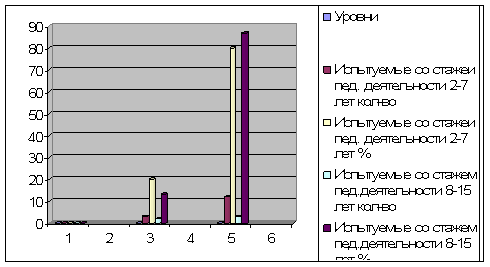
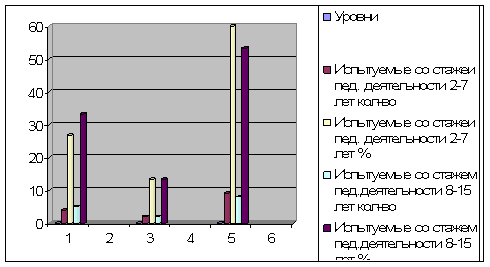
... педагогической деятельности и педагогами коррекционной школы с большим стажем педагогической деятельности. Заключение В данной курсовой работе рассматривалась тема: «Удовлетворенность трудом педагогов коррекционной школы». В теоретической части рассматривалось: структура педагогической деятельности, психологические особенности педагогов, удовлетворенность трудом, как социальная проблема. В ...
... умений и навыков при работе с глиной и пластилином, особенностей обучения навыкам лепки нами были посещены занятия по ручному труду в 1-2 классах специальной коррекционной школы по разделу лепка. Занятия были проведены соответственно программе с использованием различных методов и приёмов обучения детей лепке. Проанализировав посещённые занятия во 2 "Б" и 2 "В" классах, можно прийти к выводу, ...




0 комментариев