Навигация
2.10. Панели и меню
До сих пор приходилось иметь дело с отдельными объектами Access. И с каждым из них нужно работать в интерактивном режиме, открывая в окне базы данных вкладку требуемого объекта.
Но можно связать объекты в единое приложение. При этом вам не потребуется умение создавать сложные программы. Благодаря использованию кнопочных форм, диалоговых окон и меню работу с приложением можно автоматизировать и упростить, скрывая от пользователя ненужные в текущий момент объекты Access.
Кнопочная форма представляет собой созданную пользователем форму с кнопками. С их помощью можно, например, запускать макросы открытия форм и печати отчетов. С помощью кнопочной формы выполнить несколько действий можно, щелкнув на одной кнопке. Используя кнопочную форму и другие объекты можно объединять созданные ранее объекты базы данных в одном приложении (при этом приложение может иметь вид, отличный от внешнего вида Access). В основном кнопочная форма используется в качестве главного меню приложения. Поскольку кнопочная форма выполняет только роль меню приложения, в ней следует использовать минимальное число элементов управления. Поэтому обычно в кнопочную форму включают только кнопки, надписи, рамки объектов, линии и прямоугольники. Другие типы элементов управления, такие как текстовые поля (связанные с полями базы данных), списки, поля со списком, диаграммы и подчиненные формы, обычно в этой форме не используются. Создавая кнопочную форму, в ней следует разместить надписи, а также линии, прямоугольники или рисунки, чтобы сделать ее эстетически более привлекательной. Кнопка является простейшим элементом управления формы и используется для запуска макроса. В Access благодаря макросам, запускаемым с помощью кнопок, можно выполнять самые различные задачи.
Помимо кнопочной формы Access позволяет создать специальное меню, с помощью которого можно расширить возможности разрабатываемой системы. В это меню можно добавить часто используемые команды, а также
команды, которые уже заданы для кнопок формы. Созданное меню заменит стандартное меню Access. Специальное меню связано с формой. Можно создать одно меню и использовать его в нескольких формах.
В Access можно создать три типа меню:
Menu Bar. Обычное меню, которое может располагаться вверху формы и иметь выпадающие подменю.
Tool Bars. Группы пиктограмм, обычно располагающиеся под меню.
Shortcut Bar. Меню, всплывающие после щелчка правой кнопки мыши.
2.11. Visual Basic for Application
В Access пользователь может управлять выполнением приложении, например, изменить информацию в таблице или щелкнуть на командной кнопке. Используя в приложении макросы и процедуры, можно реализовать реакцию пользователя на эти действия. Для этого в Access предусмотрены характеристики событий для каждого элемента управления, который помещается в форму. Подключая макрос или процедуру к определенному событию элемента управления, можно не заботиться о последовательности действий, выполняемых пользователем в форме. Обработка событий представляет собой программный код, выполняемый при возникновении этого события. Код непосредственно присоединяется к форме или отчету, содержащему обрабатываемое событие.
В предыдущих версиях Access имела собственный язык Basic, называемый Access Basic. В последних версиях Access он заменен языком Visual Basic for Applications (VBA) компании Microsoft. Несмотря на некоторую схожесть, между этими языками есть существенные различия. VBA становится общим языком для всех приложений Microsoft Office. VBA является современным языком структурного программирования. Находясь в окне модулей, можно создавать и редактировать код VBA и процедуры.Visual Basic для приложений играет важную роль при разработке баз данных Access. С помощью VBA можно настроить формы и отчеты, запустить макросы, а также отобразить объект Access в других приложениях или извлечь данные. Используя Visual Basic для приложений, можно вывести формы и отчеты, выполнить методы объектов, а также создать и изменить элементы. Кроме того, имеется возможность работать с информацией непосредственно: можно создать наборы данных, задать их параметры и изменить информацию в них.
2.12 Что такое фильтр?
На наш взгляд, при изучении БД центральным понятием должен быть запрос (точнее, запрос на выборку). Ведь основное назначение БД – отвечать на запросы. Однако запрос – довольно сложное понятие. К счастью, есть понятие близкое к запросу, но более простое. Это – фильтр. По сути дела фильтр – это запрос для одной таблицы. Поэтому прежде, чем приступать к изучению запрос, уместно рассмотреть фильтр.
Что же говорится о фильтре в “пользовательских” учебниках, рассматривающих Access? В пособии С. Симоновича и др. [10] фильтр, к сожалению, не рассматривается. В учебнике под редакцией проф. Н. Макаровой о фильтре говорится следующее. “В созданной базе данных можно группировать записи разными способами, т.е. отбирать записи по условию. Для этого необходимо нажать кнопку Изменить фильтр, в появившемся окне указать в выбранных полях условия отбора, после чего после чего нажать кнопку Применить фильтр (рис. …). После применения фильтра в окне базы данных мы увидим только те записи, которые удовлетворяют условию отбора (рис. …). Кстати, условие отбора может вводиться как для одного, так и для нескольких полей.” ([7], стр. 240) Кроме этого текста, в учебнике проф. Н. Макаровой к фильтру относятся еще две иллюстрации.
На наш взгляд, этот текст обладает одним существенным изъяном. Авторы объясняют, какие кнопки и в какой последовательности нажимать, а вот для чего это делать, что получится в результате – не ясно. Что означают слова “группировать …, т.е. отбирать записи по условию”? Что, группировка и отбор – это синонимы? И затем, по какому условию отбирать? Сначала говорится, что в фильтре задается несколько условий отбора, а потом - что в результате отбираются записи, которые удовлетворяют одному условию. Что это за условия, как из нескольких условий получается одно, авторы не разъясняют.
Конечно, если школьник пришел на урок информатики, чтобы поиграть на компьютере, или посмотреть “прикольные” картинки, если “болтовню” учителя он привык пропускать мимо ушей, то ему и так сойдет. Ну, а если он задумается над словами учителя? Что он поймет из такого объяснения?
Ю.Шафрин определяет фильтр так. “Совокупность условий (логическое выражение) которую указывает пользователь для выделения некоторого подмножества строк таблицы в реляционной базе данных. Частный случай запроса” (стр. 671).
Как мы видим, и здесь наблюдается некая коллизия единственного и множественного числа. С одной стороны – много условий, а с другой – одно логическое выражение. Опять неясно, как из многих условий получается одно логическое выражение.
Обратимся к “фирменным” источникам. Надо сказать, что фирма Microsoft очень не любит разрешать пользователям копаться в “подводной части айсберга”. Она пространно объясняет, как с данным понятием работать, но неохотно и крайне невнятно объясняет, что же это понятие означает.
Help определяет фильтр так. “Набор условий, применяемых для отбора подмножества записей или для сортировки записей. В Microsoft Access существуют фильтры четырех типов: фильтр по выделенному фрагменту, обычный фильтр, расширенный фильтр и фильтр по вводу.” В свою очередь, условие отбора определяется как “набор ограничительных условий, например, = "Россия" (означающее, что требуется строковое значение "Россия") или > 30000, используемых для вывода определенного набора записей при создании запроса или фильтра.”
Итак, фильтр - это набор (или даже набор наборов) условий вида = "Россия" или > 30000. И что это такое? Ну, искушенный читатель (или пользователь) может догадаться, что на самом деле речь идет об условиях вида Х= "Россия" или У> 30000, где Х и У - это, скорее всего, атрибуты. Но что значит “набор”? Просто совокупность таких условий? Нет, скажет вдумчивый ученик, тут что-то не так. Это все равно, что сказать, что дом - это совокупность кирпичей. Но ведь все дело в том, как эти кирпичи (или условия) связаны! Скажем, Х= "Россия" AND У> 30000 - это одно, а Х= "Россия" OR У> 30000 – совсем другое.
Примерно на таком же уровне определяется фильтр и во “взрослой” литературе.
В справочнике [2] на стр. 191 говорится: “Фильтр – это набор условий, которые можно применить к данным. Применение другого фильтра к результату предыдущего дополнительно урезает результирующий набор данных.” В том же справочнике на стр. 395 фильтр определяется так. “Режим, позволяющий отображать только некоторые записи таблицы. В программе Access с помощью фильтра можно также отсортировать информацию. В отличии от запросов, фильтры не являются объектами, и не появляются в окне базы данных.”
Так что же такое фильтр: режим или набор условий? Ни то, ни другое. Оказывается это – нечто!
“Фильтр – нечто, отсеивающее определенные элементы, - одно или несколько условий, которым должна удовлетворять запись, чтобы попасть на экран.” ([8], стр. 72)
На самом деле фильтр – это просто логическое выражение. Фильтрация таблицы – это отбор тех кортежей, для которых соответствующее выражение истинно.
Здесь мы согласны с Ю.Шафриным, определяющим фильтр как логическое выражение. Нужно только пояснить, как оно строится из пресловутых “условий”. Но прежде нам придется вспомнить, что такое арифметическое выражение.
Арифметические и логические выражения
Help определяет выражение так. “Любая комбинация операторов, констант, значений текстовых констант, функций, имен полей, элементов управления или свойств, результатом которой является конкретное значение.”
Нас такое определение не устраивает. Оно не конструктивно. Мы хотели бы, чтобы по виду текста можно было бы узнать, является ли оно выражением. А как узнать, является ли результатом данной комбинации “конкретное значение”?
Попробуем найти более конструктивное определение. Чтобы не загромождать изложение непринципиальными деталями, мы ограничимся случаем, когда в таблице все атрибуты – числовые (т.е. в клетках таблицы могут стоять только числа).
Как арифметические, так и логические выражения строятся из неких “кирпичей” с помощью определенного набора операций. В случае арифметических выражений “кирпичами” служат числа и атрибуты (других “кирпичей” мы для простоты не рассматриваем), а соединяют их обычные арифметические операции. Формально арифметические выражения определяются так.
Всякое число или атрибут есть арифметическое выражение.
Если А и В - арифметические выражения, то выражения (А+В), (А-В), (А*В), (А/В) и (А**В) тоже являются арифметическими.
Символы +, -, *, / и ** интерпретируются, соответственно, как операции сложения, вычитания, умножения, деления и возведения в степень.
Вот примеры арифметических выражений: 7, х, 2+2, 2*(х+3).
Имея формальное определение, мы можем доказать, что, скажем, выражение 2*(х+3) является арифметическим. Действительно, согласно правилу 1, выражения х и 3 являются арифметическими. Отсюда, по правилу 2, следует, что выражение (х+3) тоже является арифметическим. По правилу 1, выражение 2 – арифметическое. Значит, по правилу 2, и выражение 2*(х+3) - арифметическое. В этом смысле приведенное определение конструктивно.
Переходим к определению логических выражений. Мы будем считать, что “кирпичи” логических выражений имеют вид х Т, где х – атрибут, Т – арифметическое выражение, а - один из символов сравнения: = (равно), (не равно), < (меньше) или > (больше). Соединяются они при помощи логических операций AND, OR и NOT.
Как и для арифметических выражений, мы хотим дать формальное определение. Сначала определим простейшие логические выражения, или атомы.
Определение 1. Пусть х – атрибут, Т – арифметическое выражение. Тогда выражения х=Т, хТ, хТ являются атомами.
Теперь можно формально определить логические выражения. Мы будем обозначать их большими латинскими буквами.
Определение 2.
Всякий атом есть логическое выражение.
Если Х и У - логические выражения, то выражения (Х AND У), (Х OR У) и (NOT Х) тоже являются логическими.
Вот примеры арифметических выражений: (NOT х = 7), (х = 2+2, AND у > 2*(х+3)).
Замечание 1. На практике при записи формул можно во многих случаях опускать скобки, что мы и будем делать без особых оговорок.
Теперь переходим к значениям выражений. Значениями арифметических выражений являются числа, а значениями логических выражений – Истина и Ложь.
Если мы знаем значения всех атрибутов, входящих в выражение, то мы можем вычислить и значение самого выражения. Скажем, если значение х и у есть, соответственно, 7 и 8, то значением выражения (х+2*у) есть 23. Значением атома х=(х+2*у) будет Ложь, потому что на самом деле 7 не равно 23.
Ну, а как вычислять значений логических выражений, не являющихся атомами?
Для этого служат так называемые таблицы истинности. Они позволяют вычислить значение логического выражения, если известны значения его подвыражений. Вот например таблица истинности для операции AND.
| Х | У | Х AND У |
| Истина | Истина | Истина |
| Истина | Ложь | Ложь |
| Ложь | Истина | Ложь |
| Ложь | Ложь | Ложь |
Она показывает, как, зная значения выражений Х и У, вычислить значение выражения (Х AND У).
А вот таблицы истинности для OR и NOT:
| Х | У | Х OR У |
| Истина | Истина | Истина |
| Истина | Ложь | Истина |
| Ложь | Истина | Истина |
| Ложь | Ложь | Ложь |
| Х | NOT Х |
| Истина | Ложь |
| Ложь | Истина |
Зная значения атомов, вы можете с помощью этих таблиц вычислить значение любого выражения, построив для него свою таблицу истинности. В качестве примера построим такую таблицу для выражения NOT (Х OR У)
| Х | У | Х OR У | NOT(Х OR У) |
| Истина | Истина | Истина | Ложь |
| Истина | Ложь | Истина | Ложь |
| Ложь | Истина | Истина | Ложь |
| Ложь | Ложь | Ложь | Истина |
Замечание 2. С подобными конструкциями мы встречаемся в естественных языках, например в русском. Там аналогами логических выражений являются повествовательные предложения, аналогами атомов – простые повествовательные предложения, а аналогами логических операций – слова И, ИЛИ, НЕТ и др. Конечно, аналогия здесь далеко не полная, но все же она позволяет понять основные идеи алгебры логики.
В самом деле, когда истинно предложение “На улице потемнело ИЛИ у меня устали глаза”? Когда истинно хотя бы одно из предложений “На улице потемнело” или “у меня устали глаза”. Таким образом, в данном случае ИЛИ действует аналогично операции OR (правда, в других фразах ИЛИ может употребляться в другом смысле). Точно так же союз И можно считать аналогом операции AND. Например, фраза “Вдруг заиграла музыка И в зал вошла она” истинна если и только истинны обе ее составные части: “вдруг заиграла музыка” и “в зал вошла она”. НЕ или НЕТ часто выступает аналогом операции NOT. Скажем предложение “я НЕ знаю этого человека” истинно в точности в тех случаях, когда ложна фраза “я знаю этого человека”. Вообще, язык алгебры логики можно рассматривать как попытку формализовать естественный язык.
Замечание 3. Выше мы говорили о классической, двузначной логике, когда имеется всего два значения истинности ДА и НЕТ (употребляются еще и другие обозначения, скажем ИСТИНА и ЛОЖЬ или TRUE и FALSE). Кроме двузначной логики в принципе можно рассматривать и другие логики, например трехзначную, в которой кроме ДА и НЕТ есть еще и третье значение – НЕИЗВЕСТНО (в Access оно обозначается как Null). На самом деле в Access реализована некая мешанина из двузначной и трехзначной логики. Оговоримся сразу, что мы не рекомендуем учителю выходить за рамки классической логики. Тем не менее, для полного понимания работы Access нам придется коснуться и трехзначной логики.
Наличие в Access трехзначной логики связано с тем, что в таблицах Access допускаются пустые клетки (так называемые Null-значения). Например, таблица ЗНАКОМЫЕ может выглядеть так:
| Фамилия | Имя | Отчество |
| Иванов | Петр |
(Отчество Иванова мы не знаем.)
Спрашивается, как должна такая БД отвечать на запрос “Верно ли, что у Петра Иванова отчество – Сергеевич?” Ясно, что ни ДА, ни НЕТ тут не подходит. Необходимо ввести третье значение.
Надо сказать, что попытки ввести в БД Null-значения и трехзначную логику многим авторам представляются неуместными. Вот что говорит по этому поводу известный специалист в области БД К.Дейт в своей последней монографии. “Автор данной книги разделяет мнение многих других авторов о том, что null-значения и трехзначная логика являются ошибочными понятиями и им нет места в число формальных системах, подобных реляционной модели.” ([4], стр. 544).
На наш взгляд, забивать школьнику голову трехзначной логикой и Null-значениями при изучении Access не стоит. Дай Бог ему разобраться с обычной, двузначной логикой.
Мы рекомендуем ограничиться случаем, когда таблицы не имеют пустых клеток. Можно даже установить значение ДА параметра Свойства поля/Обязательное поле. В этом случае Access будет сам следить, чтобы все клетки были заполнены. Тогда пользователь гарантирован ото всех неприятностей, связанных с Null-значениями.
Замечание 4. Обычно логику определяют как науку о правильных рассуждениях ([1, 3, 5, 9]). На наш взгляд, это не совсем верно. В вычислительной науке и, в особенности, в теории баз данных на первый план выходит другой аспект. Здесь логика используется как формальная модель естественного языка. На это, конечно, можно возразить, что язык и мышление тесно связаны. Но ведь мышление отнюдь не сводится к дедуктивным (т.е. основанным на доказательствах) методам.
Пусть логическое выражение Х не содержит атрибутов, кроме х1, х2, … , хк. Придав этим атрибутам некоторые значения, мы, тем самым, придаем числовые значения всем арифметическим выражениям, входящим в Х. Выполнив соответствующие сравнения, мы узнаем значения всех атомов, входящих в Х. Далее, с помощью таблиц истинности, мы можем вычислить и значение выражения Х.
Теперь пусть у нас есть кортеж К с атрибутами х1, х2, … , хк. Он сопоставляет каждому из этих атрибутов некоторое число. Следовательно, он обращает выражение Х либо в ИСТИНУ, либо в ЛОЖЬ.
Итак, мы доказали следующее утверждение.
Теорема 1. Пусть Х логическое выражение, не содержащее атрибутов, кроме х1, х2, …, хк, а К - кортеж с атрибутами х1, х2, … , хк. Тогда выражение Х либо истинно, либо ложно.
В первом случае мы говорим, что выражение Х ИСТИННО на кортеже К, а во втором – что оно ЛОЖНО.
Таким образом, логическое выражение можно трактовать как функцию, перерабатывающую кортеж в одно из двух значений ИСТИНА или ЛОЖЬ.
Т
еорема
1 позволяет
использовать
логические
выражения в
качестве фильтров.
Каждое такое
выражение будет
выбирать из
таблицы те
кортежи, на
которых оно
истинно.
Как задать фильтр?
Теперь переходим к процедурной части. Чтобы посмотреть фильтр (если он есть), нужно открыть соответствующую таблицу в режиме конструктора и выполнить команду “Свойства” меню Вид или контекстного меню. Откроется окно “Свойства таблицы”, в котором есть строка “Фильтр”.
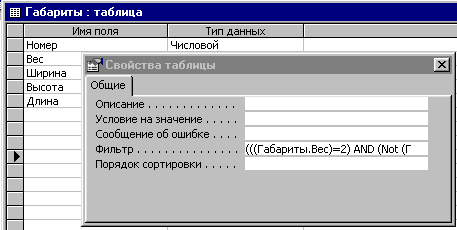
Установив курсор в поле Фильтр, вы можете распахнуть его с помощью комбинации Shift+F2.
Е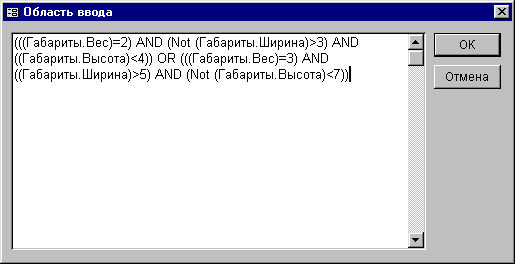
сли
фильтра еще
нет, то вы можете
создать его
прямо в этом
окне. Там же
можно и корректировать
его.
Однако, это не единственный способ задания фильтра. Вы можете воспользоваться также специальным окном “Фильтр”, вызываемым командой Записи Фильтр Расширенный фильтр.
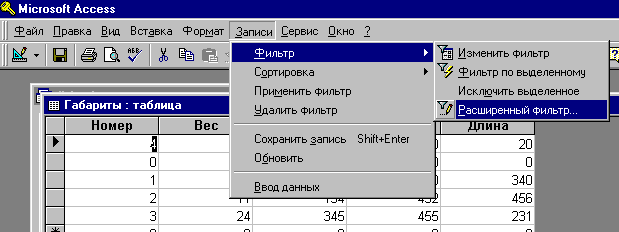
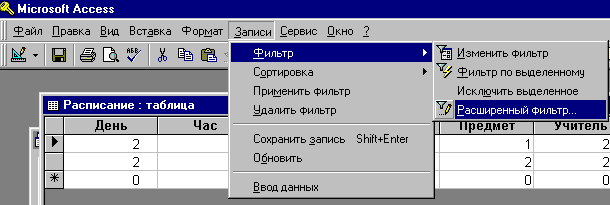
В окне “Фильтр” находится бланк QBE.
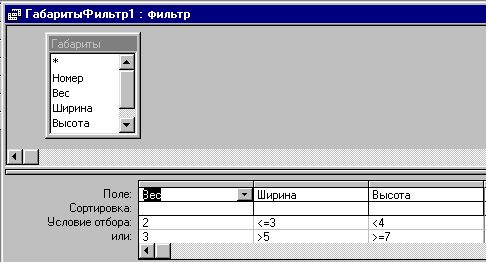
Окно фильтра состоит из двух частей. В верхней части находится схема отношения (прямоугольник, содержащий имя таблицы и перечень атрибутов). В нижней части находится бланк запроса QBE. Он содержит строку ПОЛЕ, в которой указываются атрибуты, по которым идет фильтрация, либо сортировка. Ниже располагается строка СОРТИРОВКА, в которой для некоторых атрибутов указывается порядок сортировки (по убыванию, или по возрастанию). Еще ниже располагается строка УСЛОВИЕ ОТБОРА и строки ИЛИ (из них обычно видна только одна).
На наш взгляд, сортировку стоит объяснять отдельно, и мы пока не будем ее рассматривать. Отметим также, что сортировка несколько выходит за рамки классической реляционной модели, поскольку там отношение мыслится как множество (т.е. неупорядоченный набор) кортежей. Впрочем, тот, кто прилежно изучал информатику, знает, что любая хорошая модель проще, чем соответствующая реальность.
Этот бланк удобно применять, если фильтр имеет некоторый специальный вид, о котором мы сейчас поговорим. Это так называемая дизъюнктивная нормальная форма (сокращенно – ДНФ). Она заслуживает внимание не только в связи с изучением Access, и поэтом мы уделим ей особое внимание.
Вот примеры выражений в ДНФ (мы будем для краткости называть их ДНФ-выражениями).
(Вес = 2 AND NOT (Высота >3) AND Ширина 5 AND NOT (Ширина 4 AND Высота >6 AND Ширина 80 AND NOT (Зарплата 80) AND Зарплата 80 AND NOT (Зарплата 80) AND Зарплата 80 OR NOT (Зарплата 80) AND Зарплата 3) AND Ширина 5 AND NOT (Ширина 4 AND Высота >6 AND Ширина 3
5
NOT 4
>6
Похожие работы
... для создания вычисляемых выражений в формах, отчетах и запросах. Макросы: программирование без программирования Для непрограммистов (или опытных пользователей, которые просто не желают программировать) в Access предусмотрены макросы. Они позволяют автоматизировать выполнение некоторых задач. Около пятидесяти макросов дают возможность манипулировать данными, создавать меню и диалоговые окна, ...
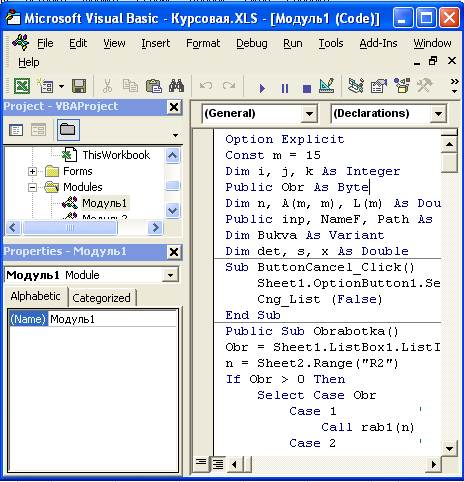
... VB или VBA. Обработка модулей VBA Проект – Файл приложения Microsoft Office, в котором написана программа VBA Приложение – Приложение Microsoft Office (Word, Excel, Access, Power Point и др.) Модуль – Именованная область в файле проекта содержащая в себе код, написанный на языке VBA Окно проекта – “дерево”, содержащее на себе все “деревья” загруженных проектов, “дерево” состоит из ...
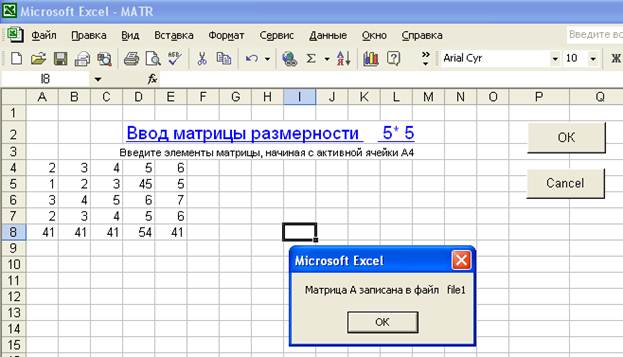
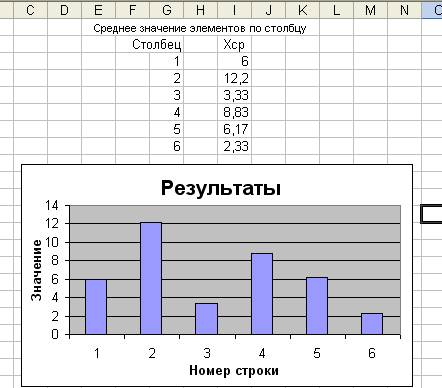
... оболочки позволяющих создавать, вести и обрабатывать любые документы и информацию. Причем информация набранная например в Excel может быть свободно перенесена в Word или наоборот. Табличный процессор Excel 7.0 Табличный процессор Excel фирмы Microsoft предназначен для ввода хранения обсчета и выдачи больших обьемов данных в виде удобном для анализа и восприятия информации. Все данные хранятся и ...
... для реализации системы бюджетирования Консультационной группы "Воронов и Максимов". Статья о проблемах выбора системы бюджетирования - в проекте "УПРАВЛЕНИЕ 3000". Бюджетный автомат Если вы решитесь на автоматизацию системы бюджетирования компании, перед вами сразу встанут вопросы: что выбрать, сколько платить, как внедрять. Примеряйте! О ЧЕМ РЕЧЬ В “Капитале” на стр. 44, 45 мы рассказали ...
0 комментариев