Навигация
Ключ является массивом из восьми 32-битных элементов кода, далее в
1. Ключ является массивом из восьми 32-битных элементов кода, далее в
настоящей работе он обозначается символом К: . В ГОСТе элементы ключа
используются как 32-разрядные целые числа без знака: . Таким образом, размер
ключа составляет 32·8=256 бит или 32 байта.
2. Таблица замен является матрицей 8ґ16, содержащей 4-битовые элементы,
которые можно представить в виде целых чисел от 0 до 15. Строки таблицы замен
называются узлами замен, они должны содержать различные значения, то есть каждый
узел замен должен содержать 16 различных чисел от 0 до 15 в произвольном
порядке. В настоящей статье таблица замен обозначается символом H: . Таким
образом, общий объем таблицы замен равен: 8 узлов ґ 16 элементов/узел ґ 4
бита/элемент = 512 бит или 64 байта.
Основной шаг криптопреобразования.
Основной шаг криптопреобразования по своей сути является оператором,
определяющим преобразование 64-битового блока данных. Дополнительным параметром
этого оператора является 32-битовый блок, в качестве которого используется
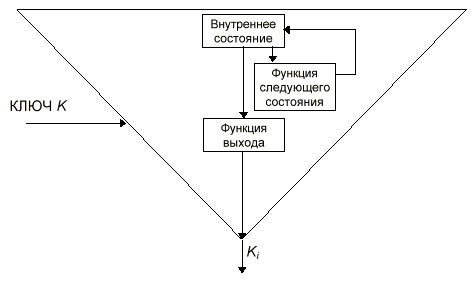
какой-либо элемент ключа. Схема алгоритма основного шага приведена на рисунке 1.
Ниже даны пояснения к алгоритму основного шага:
Определяет исходные данные для основного шага криптопреобразования:
N–преобразуемый 64-битовый блок данных, в ходе выполнения шага его младшая
(N1) и старшая (N2) части обрабатываются как отдельные 32-битовые целые
числа без знака. Таким образом, можно записать N=(N1,N2).
X–32-битовый элемент ключа;
Сложение с ключом. Младшая половина преобразуемого блока складывается по
модулю 232 с используемым на шаге элементом ключа, результат передается на
следующий шаг;
Поблочная замена. 32-битовое значение, полученное на предыдущем шаге,
интерпретируется как массив из восьми 4-битовых блоков кода:
S=(S0,S1,S2,S3,S4,S5,S6,S7).
значение каждого из восьми блоков заменяется на новое, которое выбирается по
таблице замен следующим образом: значение блока Si заменяется на Si-тый по
порядку элемент (нумерация с нуля) i-того узла замен (т.е. i-той строки
таблицы замен, нумерация также с нуля). Другими словами, в качестве замены для
значения блока выбирается элемент из таблицы замен с номером строки, равным
номеру заменяемого блока, и номером столбца, равным значению заменяемого блока
как 4-битового целого неотрицательного числа. Теперь становится понятным
размер таблицы замен: число строк в ней равно числу 4-битных элементов в
32-битном блоке данных, то есть восьми, а число столбцов равно числу различных
значений 4-битного блока данных, равному как известно 24, шестнадцати.
Циклический сдвиг на 11 бит влево. Результат предыдущего шага сдвигается
циклически на 11 бит в сторону старших разрядов и передается на следующий шаг.
На схеме алгоритма символом ?11 обозначена функция циклического сдвига своего
аргумента на 11 бит в сторону старших разрядов.
Побитовое сложение: значение, полученное на шаге 3, побитно складывается по
модулю 2 со старшей половиной преобразуемого блока.
Сдвиг по цепочке: младшая часть преобразуемого блока сдвигается на место
старшей, а на ее место помещается результат выполнения предыдущего шага.
Полученное значение преобразуемого блока возвращается как результат выполнения
алгоритма основного шага криптопреобразования.
Базовые циклы криптографических преобразований.
Как отмечено в начале настоящей статьи, ГОСТ относится к классу блочных шифров,
то есть единицей обработки информации в нем является блок данных. Следовательно,
вполне логично ожидать, что в нем будут определены алгоритмы для
криптографических преобразований, то есть для зашифрования, расшифрования и
"учета" в контрольной комбинации одного блока данных. Именно эти алгоритмы и
называются базовыми циклами ГОСТа, что подчеркивает их фундаментальное значение
для построения этого шифра.
Базовые циклы построены из основных шагов криптографического преобразования,
рассмотренного в предыдущем разделе. В процессе выполнения основного шага
используется только один элемент ключа, в то время как ключ ГОСТ содержит восемь
таких элементов. Следовательно, чтобы ключ был использован полностью, каждый из
базовых циклов должен многократно выполнять основной шаг с различными его
элементами. Вместе с тем кажется вполне естественным, что в каждом базовом цикле
все элементы ключа должны быть использованы одинаковое число раз, по
соображениям стойкости шифра это число должно быть больше одного.
Все сделанные выше предположения, опирающиеся просто на здравый смысл, оказались
верными. Базовые циклы заключаются в многократном выполнении основного шага с
использованием разных элементов ключа и отличаются друг от друга только числом
повторения шага и порядком использования ключевых элементов. Ниже приведен этот
порядок для различных циклов.
Цикл зашифрования 32-З:
K0,K1,K2,K3,K4,K5,K6,K7,K0,K1,K2,K3,K4,K5,K6,K7,K0,K1,K2,K3,K4,K5,K6,K7,K7,K6,K5,K4,K3,K2,K1,K0.
Цикл расшифрования 32-Р:
K0,K1,K2,K3,K4,K5,K6,K7,K7,K6,K5,K4,K3,K2,K1,K0,K7,K6,K5,K4,K3,K2,K1,K0,K7,K6,K5,K4,K3,K2,K1,K0.
Цикл выработки имитовставки 16-З:
K0,K1,K2,K3,K4,K5,K6,K7,K0,K1,K2,K3,K4,K5,K6,K7.
Каждый из циклов имеет собственное буквенно-цифровое обозначение,
соответствующее шаблону "n-X", где первый элемент обозначения (n), задает число
повторений основного шага в цикле, а второй элемент обозначения (X), буква,
задает порядок зашифрования ("З") или расшифрования ("Р") в использовании
ключевых элементов. Этот порядок нуждается в дополнительном пояснении:
Цикл расшифрования должен быть обратным циклу зашифрования, то есть
последовательное применение этих двух циклов к произвольному блоку должно дать в
итоге исходный блок, что отражается следующим соотношением: Ц32-Р(Ц32-З(T))=T,
где T – произвольный 64-битный блок данных, ЦX(T) – результат выполнения цикла X
над блоком данных T. Для выполнения этого условия для алгоритмов, подобных
ГОСТу, необходимо и достаточно, чтобы порядок использования ключевых элементов
соответствующими циклами был взаимно обратным. В справедливости записанного
условия для рассматриваемого случая легко убедиться, сравнив приведенные выше
последовательности для циклов 32-З и 32-Р. Из сказанного вытекает одно
интересное следствие: свойство цикла быть обратным другому циклу является
взаимным, то есть цикл 32-З является обратным по отношению к циклу 32-Р. Другими
словами, зашифрование блока данных теоретически может быть выполнено с помощью
цикла расшифрования, в этом случае расшифрование блока данных должно быть
выполнено циклом зашифрования. Из двух взаимно обратных циклов любой может быть
использован для зашифрования, тогда второй должен быть использован для
расшифрования данных, однако стандарт ГОСТ28147-89 закрепляет роли за циклами и
не предоставляет пользователю права выбора в этом вопросе.
Цикл выработки имитовставки вдвое короче циклов шифрования, порядок
использования ключевых элементов в нем такой же, как в первых 16 шагах цикла
зашифрования, в чем нетрудно убедиться, рассмотрев приведенные выше
последовательности, поэтому этот порядок в обозначении цикла кодируется той же
самой буквой "З".
Схемы базовых циклов приведены на рисунках 2а-в. Каждый из них принимает в
качестве аргумента и возвращает в качестве результата 64-битный блок данных,
обозначенный на схемах N. Символ Шaг(N,X) обозначает выполнение основного шага
криптопреобразования для блока N с использованием ключевого элемента X. Между
циклами шифрования и вычисления имитовставки есть еще одно отличие, не
упомянутое выше: в конце базовых циклов шифрования старшая и младшая часть блока
результата меняются местами, это необходимо для их взаимной обратимости.
Основные режимы шифрования.
ГОСТ 28147-89 предусматривает три следующих режима шифрования данных:
простая замена,
гаммирование,
гаммирование с обратной связью,
и один дополнительный режим выработки имитовставки.
В любом из этих режимов данные обрабатываются блоками по 64 бита, на которые
разбивается массив, подвергаемый криптографическому преобразованию, именно
поэтому ГОСТ относится к блочным шифрам. Однако в двух режимах гаммирования есть
возможность обработки неполного блока данных размером меньше 8 байт, что
существенно при шифровании массивов данных с произвольным размером, который
может быть не кратным 8 байтам.
Прежде чем перейти к рассмотрению конкретных алгоритмов криптографических
преобразований, необходимо пояснить обозначения, используемые на схемах в
следующих разделах:
Tо,Tш– массивы соответственно открытых и зашифрованных данных;
, – i-тые по порядку 64-битные блоки соответственно открытых и зашифрованных
данных: , ??i?n, последний блок может быть неполным: ;
n –число 64-битных блоков в массиве данных;
ЦX– функция преобразования 64-битного блока данных по алгоритму базового цикла
"X";
Теперь опишем основные режимы шифрования:
Простая замена.
Зашифрование в данном режиме заключается в применении цикла 32-З к блокам
открытых данных, расшифрование – цикла 32-Р к блокам зашифрованных данных. Это
наиболее простой из режимов, 64-битовые блоки данных обрабатываются в нем
независимо друг от друга. Схемы алгоритмов зашифрования и расшифрования в режиме
простой замены приведены на рисунках 3а и б соответственно, они тривиальны и не
нуждаются в комментариях.
Размер массива открытых или зашифрованных данных, подвергающийся соответственно
зашифрованию или расшифрованию, должен быть кратен 64 битам: Tо=Tш=64·n, после
выполнения операции размер полученного массива данных не изменяется.
Режим шифрования простой заменой имеет следующие особенности:
Так как блоки данных шифруются независимо друг от друга и от их позиции в
массиве, при зашифровании двух одинаковых блоков открытого текста получаются
одинаковые блоки шифротекста и наоборот. Отмеченное свойство позволит
криптоаналитику сделать заключение о тождественности блоков исходных данных,
если в массиве зашифрованных данных ему встретились идентичные блоки, что
является недопустимым для серьезного шифра.
Если длина шифруемого массива данных не кратна 8 байтам или 64 битам,
возникает проблема, чем и как дополнять последний неполный блок данных массива
до полных 64 бит. Эта задача не так проста, как кажется на первый взгляд,
поскольку очевидные решения типа "дополнить неполный блок нулевыми битами"
или, более обще, "дополнить неполный блок фиксированной комбинацией нулевых и
единичных битов" могут при определенных условиях дать в руки криптоаналитика
возможность методами перебора определить содержимое этого самого неполного
блока, и этот факт означает снижение стойкости шифра. Кроме того, длина
шифротекста при этом изменится, увеличившись до ближайшего целого, кратного 64
битам, что часто бывает нежелательным.
первый взгляд, перечисленные выше особенности делают практически невозможным
использование режима простой замены, ведь он может применяться только для
шифрования массивов данных с размером кратным 64 битам, не содержащим
повторяющихся 64-битных блоков. Кажется, что для любых реальных данных
гарантировать выполнение указанных условий невозможно. Это почти так, но есть
одно очень важное исключение: вспомните, что размер ключа составляет 32 байта,
а размер таблицы замен – 64 байта. Кроме того, наличие повторяющихся
8-байтовых блоков в ключе или таблице замен будет говорить об их весьма плохом
качестве, поэтому в реальных ключевых элементах такого повторения быть не
может. Таким образом мы выяснили, что режим простой замены вполне подходит для
шифрования ключевой информации, тем более, что прочие режимы для этой цели
менее удобны, поскольку требуют наличия дополнительного синхронизирующего
элемента данных – синхропосылки (см. следующий раздел). Наша догадка верна,
ГОСТ предписывает использовать режим простой замены исключительно для
шифрования ключевых данных.
Гаммирование.
Как же можно избавиться от недостатков режима простой замены? Для этого
необходимо сделать возможным шифрование блоков с размером менее 64 бит и
обеспечить зависимость блока шифротекста от его номера, иными словами,
рандомизировать процесс шифрования. В ГОСТе это достигается двумя различными
способами в двух режимах шифрования, предусматривающих гаммирование.
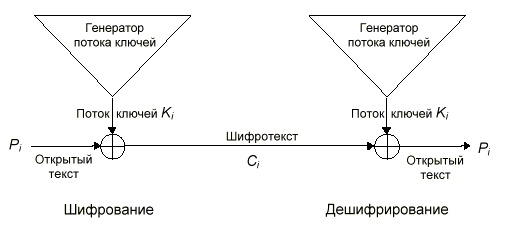
Гаммирование – это наложение (снятие) на открытые (зашифрованные) данные
криптографической гаммы, то есть последовательности элементов данных,
вырабатываемых с помощью некоторого криптографического алгоритма, для получения
зашифрованных (открытых) данных. Для наложения гаммы при зашифровании и ее
снятия при расшифровании должны использоваться взаимно обратные бинарные
операции, например, сложение и вычитание по модулю 264 для 64-битных блоков
данных. В ГОСТе для этой цели используется операция побитного сложения по модулю
2, поскольку она является обратной самой себе и к тому же наиболее просто
реализуется. Гаммирование решает обе упомянутые проблемы; во первых, все
элементы гаммы различны для реальных шифруемых массивов и, следовательно,
результат зашифрования даже двух одинаковых блоков в одном массиве данных будет
различным. Во вторых, хотя элементы гаммы и вырабатываются одинаковыми порциями
в 64 бита, использоваться может и часть такого блока с размером, равным размеру
шифруемого блока.
Теперь перейдем непосредственно к описанию режима гаммирования. Гамма для этого
режима получается следующим образом: с помощью некоторого алгоритмического
рекуррентного генератора последовательности чисел (РГПЧ) вырабатываются
64-битные блоки данных, которые далее подвергаются преобразованию по циклу 32-З,
то есть зашифрованию в режиме простой замены, в результате получаются блоки
гаммы. Благодаря тому, что наложение и снятие гаммы осуществляется при помощи
одной и той же операции побитового исключающего или, алгоритмы зашифрования и
расшифрования в режиме гаммирования идентичны, их общая схема приведена на
рисунке 5.
РГПЧ, используемый для выработки гаммы, является рекуррентной функцией:
?i+1=f(?i), где ?i – элементы рекуррентной последовательности, f – функция
преобразования. Следовательно, неизбежно возникает вопрос о его инициализации,
то есть об элементе ?0. В действительности, этот элемент данных является
параметром алгоритма для режимов гаммирования, на схемах он обозначен как S, и
называется в криптографии синхропосылкой, а в нашем ГОСТе – начальным
заполнением одного из регистров шифрователя. По определенным соображениям
разработчики ГОСТа решили использовать для инициализации РГПЧ не непосредственно
синхропосылку, а результат ее преобразования по циклу 32-З: ?0=Ц32-З(S).
Последовательность элементов, вырабатываемых РГПЧ, целиком зависит от его
начального заполнения, то есть элементы этой последовательности являются
функцией своего номера и начального заполнения РГПЧ: ?i=fi(?0), где
fi(X)=f(fi–1(X)), f0(X)=X. С учетом преобразования по алгоритму простой замены
добавляется еще и зависимость от ключа:
Гi=Ц32-З(?i)=Ц32-З(fi(?0))=Ц32-З(fi(Ц32-З(S)))=?i(S,K), где Гi – i-тый элемент
гаммы, K – ключ.
Таким образом, последовательность элементов гаммы для использования в режиме
гаммирования однозначно определяется ключевыми данными и синхропосылкой.
Естественно, для обратимости процедуры шифрования в процессах за- и
расшифрования должна использоваться одна и та же синхропосылка. Из требования
уникальности гаммы, невыполнение которого приводит к катастрофическому снижению
стойкости шифра, следует, что для шифрования двух различных массивов данных на
одном ключе необходимо обеспечить использование различных синхропосылок. Это
приводит к необходимости хранить или передавать синхропосылку по каналам связи
вместе с зашифрованными данными, хотя в отдельных особых случаях она может быть
предопределена или вычисляться особым образом, если исключается шифрование двух
массивов на одном ключе.
Теперь подробно рассмотрим РГПЧ, используемый в ГОСТе для генерации элементов
гаммы. Прежде всего надо отметить, что к нему не предъявляются требования
обеспечения каких-либо статистических характеристик вырабатываемой
последовательности чисел. РГПЧ спроектирован разработчиками ГОСТа исходя из
необходимости выполнения следующих условий:
период повторения последовательности чисел, вырабатываемой РГПЧ, не должен
сильно (в процентном отношении) отличаться от максимально возможного при
заданном размере блока значения 264;
соседние значения, вырабатываемые РГПЧ, должны отличаться друг от друга в
каждом байте, иначе задача криптоаналитика будет упрощена;
РГПЧ должен быть достаточно просто реализуем как аппаратно, так и программно
на наиболее распространенных типах процессоров, большинство из которых, как
известно, имеют разрядность 32 бита.
Исходя из перечисленных принципов создатели ГОСТа спроектировали весьма
удачный РГПЧ, имеющий следующие характеристики:
64-битовом блоке старшая и младшая части обрабатываются независимо друг от
друга: , фактически, существуют два независимых РГПЧ для старшей и младшей
частей блока.
рекуррентные соотношения для старшей и младшей частей следующие:
, где C1=101010116;
, где C2=101010416;
Нижний индекс в записи числа означает его систему счисления, таким образом,
константы, используемые на данном шаге, записаны в 16-ричной системе
счисления.
Второе выражение нуждается в комментариях, так как в тексте ГОСТа приведено
нечто другое: , с тем же значением константы C2. Но далее в тексте стандарта
дается комментарий, что, оказывается, под операцией взятия остатка по модулю
232–1 там понимается не то же самое, что и в математике. Отличие заключается в
том, что согласно ГОСТу (232–1)mod(232–1)=(232–1), а не 0. На самом деле, это
упрощает реализацию формулы, а математически корректное выражение для нее
приведено выше.
период повторения последовательности для младшей части составляет 232, для
старшей части 232–1, для всей последовательности период составляет
232?(232–1), доказательство этого факта, весьма несложное, получите сами.
Первая формула из двух реализуется за одну команду, вторая, несмотря на ее
кажущуюся громоздкость, за две команды на всех современных 32-разрядных
процессорах.
алгоритма шифрования в режиме гаммирования приведена на рисунке 4, ниже
изложены пояснения к схеме:
0.Определяет исходные данные для основного шага криптопреобразования:
Tо(ш) – массив открытых (зашифрованных) данных произвольного размера,
подвергаемый процедуре зашифрования (расшифрования), по ходу процедуры
массив подвергается преобразованию порциями по 64 бита;
S– синхропосылка, 64-битный элемент данных, необходимый для инициализации
генератора гаммы;
1.Начальное преобразование синхропосылки, выполняемое для ее "рандомизации",
то есть для устранения статистических закономерностей, присутствующих в ней,
результат используется как начальное заполнение РГПЧ;
2.Один шаг работы РГПЧ, реализующий его рекуррентный алгоритм. В ходе данного
шага старшая (S1) и младшая (S0) части последовательности данных
вырабатываются независимо друг от друга;
3.Гаммирование. Очередной 64-битный элемент, выработанный РГПЧ, подвергается
процедуре зашифрования по циклу 32–З, результат используется как элемент гаммы
для зашифрования (расшифрования) очередного блока открытых (зашифрованных)
данных того же размера.
4.Результат работы алгоритма – зашифрованный (расшифрованный) массив данных.
Ниже перечислены особенности гаммирования как режима шифрования.
1. Одинаковые блоки в открытом массиве данных дадут при зашифровании
различные блоки шифротекста, что позволит скрыть факт их идентичности.
2. Поскольку наложение гаммы выполняется побитно, шифрование неполного
блока данных легко выполнимо как шифрование битов этого неполного блока, для
чего используется соответствующие биты блока гаммы . Так, для зашифрования
неполного блока в 1 бит можно использовать любой бит из блока гаммы.
Похожие работы
... версия программы, осуществляющей шифрование информации. В дальнейшем предполагается разработка и усовершенствование комплекса программ, обеспечивающих защиту информации от несанкционированного доступа. В процессе разработки были закреплены навыки шифрования информации по ГОСТ 28147-89 и программирования на ассемблере. Библиографический список 1. Конспект лекций по курсу «Кодирование и ...
... которым они имели место, является одним из необходимых условий разработки защищенных систем и их использования.АЛГОРИТМ RC4 В настоящей работе проведен анализ криптостойкости методов защиты информации, применяемых в операционных системах семейства Microsoft Windows 95, 98. Кроме того, нами было проведено исследование по поиску необходимой длины ключа и пароля, а также были рассмотрены проблемы ...
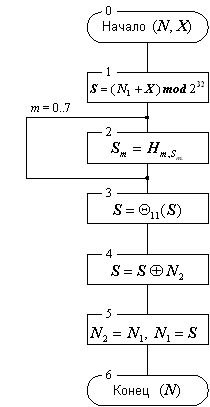


0 комментариев