Навигация
ОБОСНОВАНИЕ ВЫБОРА ЯЗЫКА ПРОГРАММИРОВАНИЯ
6. ОБОСНОВАНИЕ ВЫБОРА ЯЗЫКА ПРОГРАММИРОВАНИЯ
Язык Borland Pascal 7.0 обладает свойствами использования графики, строковых типов и констант, любых видов переменных, имеет возможность использования модулей (как уже существующих, так и созданных пользователями). Язык Borland Pascal 7.0 - язык высокого уровня, на нем писать программы намного удобнее так, как языки высокого уровня имеют резервированные слова, которые замещают ряд кодовых символов на языках низкого уровня. Язык Borland Pascal 7.0 имеет практичный интерфейс, который позволяет быстро и удобно совершить те или иные действия. Мой выбор остановился на этом языке.
7. РЕШЕНИЕ ЗАДАЧИ ТЕСТА ДЛЯ
НАПИСАНИЯ И ОТЛАДКИ ПРОГРАММЫДля нашей конкретной задачи ресурсные ограничения имеют вид:
1.2X1 + 1.8X2 + 2.4X3 768
2.4X1 + 1.2X3 + 2.4X4 600
1.2X2 + 1.2X3 + 1.2X4 480
Ограничения по комплектности:
| A1 2 A2 1 A1 = 2A2 | A3 4 A4 1 A3 = 4A4 |
Отсюда составляем систему уравнений:
X1 - 2X2 = 0
X3 - 4X4 = 0
Итак, система ограничений задачи состоит из 5 уравнений и целевой функции:
Fmax = X1+X2+X3+X4
Приводим систему к каноническому виду:
1.2X1 + 1.8X2 + 2.4X3 +X5 768
2.4X1 + 1.2X3 + 2.4X4 +X6 600
1.2X2 + 1.2X3 + 1.2X4 +X7 480
X1 - 2X2 +Y1 = 0
X3 - 4X4 +Y2 = 0
Приводим целевую функцию к каноническому виду:
Fmax = X1+X2+X3+X4 + 0X5+0X6+0X7-My1-My2
Так как введены искусственные переменные – исследуем на минимум.
Fmin = -X1-X2-X3-X4 - 0X5-0X6-0X7+My1+My2
Таблица 7.1
Симплекс таблица
| | -1 | -1 | -1 | -1 | 0 | 0 | 0 | M | M | ||
| C | Б | H | X1 | X2 | X3 | X4 | X5 | X6 | X7 | Y1 | Y2 |
| 0 0 0 M M | X5 X6 X7 Y1 Y2 | 768 600 480 0 0 | 1.2 2.4 0 1 0 | 1.8 0 1.2 -2 0 | 2.4 1.2 1.2 0 1 | 0 2.4 1.2 0 -4 | 1 0 0 0 0 | 0 1 0 0 0 | 0 0 1 0 0 | 0 0 0 1 0 | 0 0 0 0 1 |
| | 0 | 1 | -2 | 1 | -4 | 0 | 0 | 0 | 0 | 0 | |
| 0 0 0 M -1 | X5 X6 X7 Y1 X3 | 768 600 480 0 0 | 1.2 2.4 0 1 0 | 1.8 0 1.2 -2 0 | 0 0 0 0 1 | 9.6 7.2 6.0 0 -4 | 1 0 0 0 0 | 0 1 0 0 0 | 0 0 1 0 0 | 0 0 0 1 0 | |
| | 0 | 1 | -2 | 0 | 0 | 0 | 0 | 0 | 0 | ||
| 0 0 0 -1 -1 | X5 X6 X7 X1 X3 | 768 600 480 0 0 | 0 0 0 1 0 | 4.2 4.8 1.2 -2 0 | 0 0 0 0 1 | 9.6 7.2 6.0 0 -4 | 1 0 0 0 0 | 0 1 0 0 0 | 0 0 1 0 0 | ||
| | 0 | 0 | 3 | 0 | 5 | 0 | 0 | 0 | |||
| 0 0 -1 -1 -1 | X5 X6 X4 X1 X3 | 0 24 80 0 320 | 0 0 0 1 0 | 2.28 3.36 0.2 -2 0.8 | 0 0 0 0 1 | 0 0 1 0 0 | 1 0 0 0 0 | 0 1 0 0 0 | -1.6 -1.2 0.16 0 0.66 | ||
| | -400 | 0 | 2 | 0 | 0 | 0 | 0 | -0.83 | |||
| -1 0 -1 -1 -1 | X2 X6 X4 X1 X3 | 0 24 80 0 320 | 0 0 0 1 0 | 1 0 0 0 0 | 0 0 0 0 1 | 0 0 1 0 0 | 0.43 -1.47 -0.08 0.87 -0.35 | 0 1 0 0 0 | -0.7 1.15 0.3 -1.4 1.22 | ||
| | -400 | 0 | 0 | 0 | 0 | -0.87 | 0 | 0.57 | |||
| -1 0 -1 -1 -1 | X2 X7 X4 X1 X3 | 14.54 20.72 73.63 29.08 294.5 | 0 0 0 1 0 | 1 0 0 0 0 | 0 0 0 0 1 | 0 0 1 0 0 | -0.45 -1.27 0.3 -0.9 1.21 | 0.6 0.86 -0.26 1.21 -1.06 | 0 1 0 0 0 | ||
| -410 | 0 | 0 | 0 | 0 | -0.15 | -0.49 | 0 |
Индексная строка при исследовании на минимум не содержит положительных элементов, значит, получено оптимальное решение:
Fmax = - Fmin = 410 – максимально возможный выпуск продукции (шт).
X1 = 29, 08 – Детали А1 (шт).
X2 = 14, 54 – Детали А2 (шт).
X3 = 294, 52 – Детали А3 (шт).
X4 = 73, 63 – Детали А4 (шт).
X7 = 20, 72 – Недостающие ресурсы (станко-часы).
Похожие работы
... положит в такой симплекс-таблице текущие базисные переменные равными Ai,0, а свободные - нулю, то будет получено оптимальное решение. Практика применения симплекс метода показала, что число итераций, требуемых для решения задачи линейного программирования обычно колеблется от 2m до 3m, хотя для некоторых специально построенных задач вычисления по правилам симплекс метода превращаются в прямой ...
... и подставляя её во всех остальных равенствах и неравенствах (а также в функции f).Такую задачу называют «основной» или «стандартной» в линейном программировании. 1.2 Решение задач линейного программирования симплекс-методом Задача ЛП в общем виде может быть записана так: (c, x) − max Ax = b, где c =(c1,c2,...,cn)T – мерный вектор-столбец коэффициентов; x =(x1,x2,...,xn)T – ...
... под названием метода обратной матрицы или модифицированного симплекс-метода. При решении задач линейного программирования, в которых n (количество переменных) существенно больше m (количество ограничений), улучшенный симплекс-метод требует по сравнению с другими значительно меньшего количества вычислительных операций и объема памяти ЭВМ. В улучшенном симплекс-методе реализуется та же основная ...
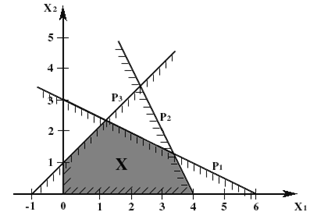
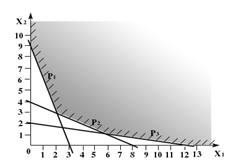
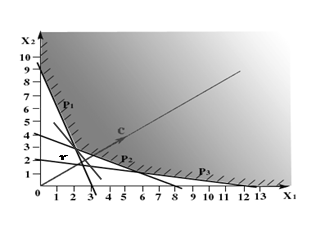
... ограничения несовместны, множество планов пусто и задача ЛП решения не имеет. Рис. 1.4 Рис. 1.5 Рис. 1.6 2. Симплекс-метод 2.1 Идея симплекс-метода Рассмотрим универсальный метод решения канонической задачи линейного программирования , , , с n переменными и m ограничениями-равенствами, известный как симплекс-метод. Множество планов канонической задачи – ...

0 комментариев