Навигация
3. Спецификации
| Имя переменной | Тип | Назначение |
| n | int | Число разбиений отрезка [a, b] |
| i | int | Счетчик циклов |
| a | float | Нижний предел интегрирования |
| b | float | Верхний предел интегрирования |
| h | float | Шаг разбиения отрезка |
| e | float | Допустимая относительная ошибка |
| f | float (*) | Указатель на интегрируемую фун - цию |
| s_ab | float | Сумма значений фун – ции в точках a и b |
| s_even | float | Сумма значений фун – ции в нечетных точках |
| s_odd | float | Сумма значений фун – ции в четных точках |
| s_res | float | Текущий результат интегрирования |
| s_pres | float | Предыдущий результат интегрирования |
4. Листинг программы
#include <stdio.h>
#include <math.h>
/* Прототип фун – ции, вычисляющей интеграл */
float integral(float, float, float, float (*)(float));
/* Прототип фун – ции, задающей интегрируемую фун – цию */
float f(float);
main()
{
float result;
result = integral(0, 6, .1, f);
printf("%f", result);
return 0;
}
/* Реализация фун – ции, задающей интегрируемую фун – цию */
float f(float x)
{
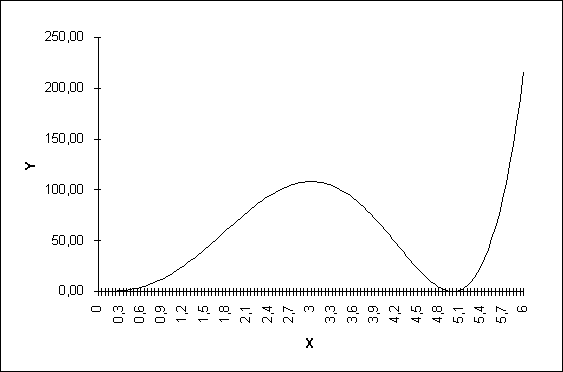
/* Функция f(x) = x³(x - 5)² */
return pow(x, 3) * pow(x - 5, 2);
}
/* Реализация фун – ции, вычисляющей интеграл */
float integral(float a, float b, float e, float (*f)(float))
{
int n = 4, i; /* Начальное число разбиений 4 */
float s_ab = f(a) + f(b); /* Сумма значений фун – ции в a и b */
float h = (b – a) / n; /* Вычисляем шаг */
float s_even = 0, s_odd;
float s_res = 0, s_pres;
/* Сумма значений фун – ции в нечетных точках */
for (i = 2; i < n; i += 2) {
s_even += f(a + i * h);
}
do {
s_odd = 0;
s_pres = s_res;
/* Сумма значений фун – ции в четных точках */
for (i = 1; i < n; i += 2) {
s_odd += f(a + i * h);
}
/* Подсчет результата */
s_res = h / 3 * (s_ab + 2 * s_even + 4 * s_odd);
/* Избегаем деления на ноль */
if (s_res == 0) s_res = e;
s_even += s_odd;
n *= 2;
h /= 2;
} while (fabs((s_pres - s_res) / s_res) > e);/* Выполнять до тех пор, пока результат не будет удовлетворять допустимой ошибке */
return fabs(s_res); /* Возвращаем результат */
}
5. Ручной счет
Таблица константных значений для n = 8
| Имя переменной | Значение |
| a | 0 |
| b | 6 |
| e | .1 |
| s_ab | 216 |
| h | .75 |
Подсчет s_even
| i | a + i * h | f(a + i * h) | s_even |
| 2 | 1.5 | 41.34375 | 41.34375 |
| 4 | 3 | 108 | 149.34375 |
| 6 | 4.5 | 22.78125 | 172.125 |
Подсчет s_odd
| i | a + i * h | f(a + i * h) | s_odd |
| 1 | .75 | 7.62012 | 7.62012 |
| 3 | 2.25 | 86.14158 | 93.7617 |
| 5 | 3.75 | 82.3973 | 176.159 |
| 7 | 5.25 | 9.044 | 185.203 |
Подсчет s_res
| ò f(x) dx | s_res = h / 3 * (s_ab + 2 * s_even + 4 * s_odd) | Абсолютная ошибка |
| 324 | 325.266 | 1.266 |
Похожие работы
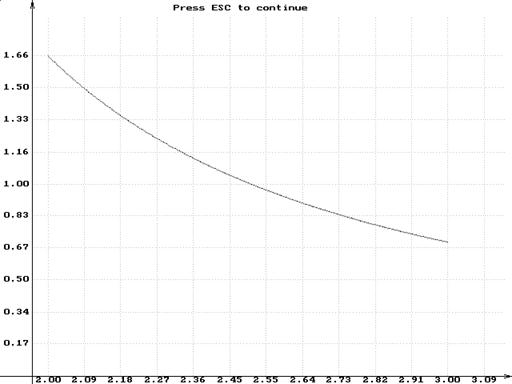
... , т. е. знакопостоянна. рис. 2 Для выполнения поставленной задачи составлена нижеописанная программа, приближенно вычисляющая определенный интеграл с помощью формулы Симпсона. Программа состоит из трех функций main, f и integral. Функция main вызывает функцию integral для вычисления интеграла и распечатывает на экране результат. Функция f принимает аргумент x типа float и возвращает значение ...
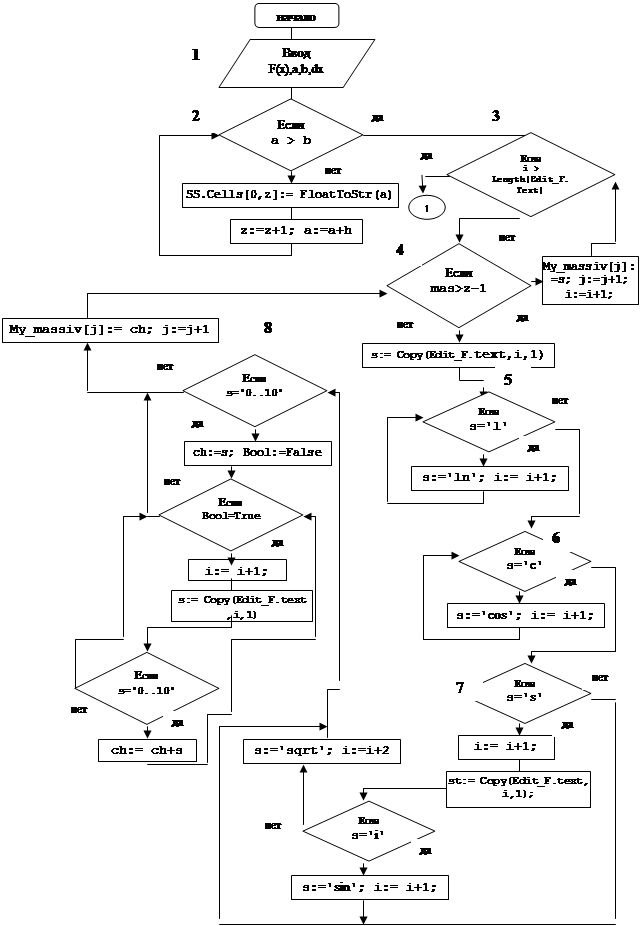
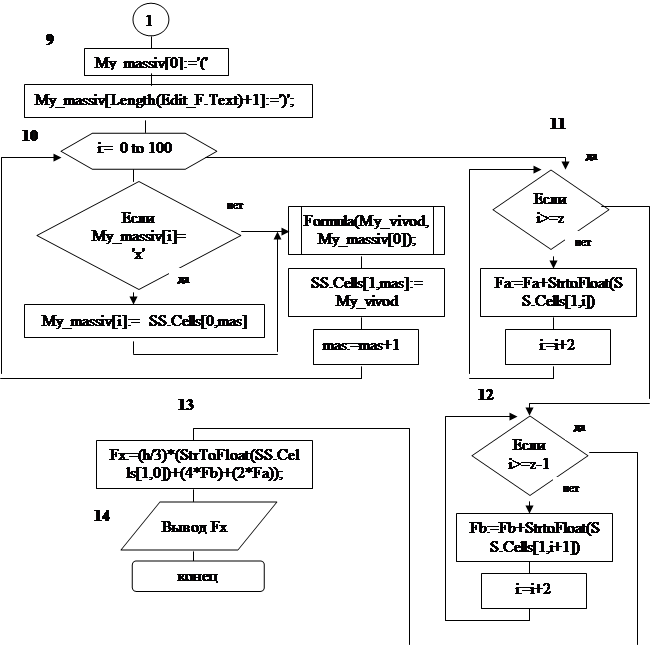
... значение разности текущего и предыдущего значений интегрирования меньше чем 0.001, если да, то выход из цикла, если нет, то переход на блок 13. Блок 15. Вывод результатов, полученных при вычислении интеграла методом Симпсона на экран. Блок 16. Конец программы. 5. Текст программы program tr_s; uses crt,graph; var a,b:real; { Границы отрезка } r,r2:real; { Предыдущее и ...
... этом отрезке функция непрерывна. Для выполнения поставленной задачи составлена нижеописанная программа, приближенно вычисляющая определенный интеграл с помощью метода трапеций. Программа состоит из трех функций main, f и trap. Функция main позволяет ввести интервалы интегрирования и задать точность вычисления интеграла, а также вызывает функцию trap для вычисления интеграла и распечатывает на ...
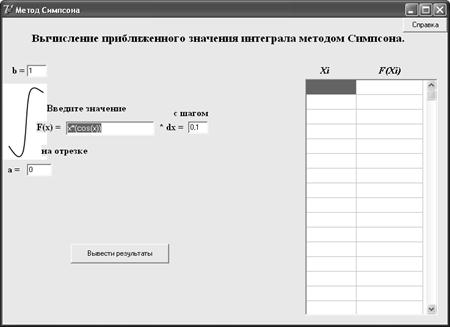
... из 1 откомпилированного exe файла – Метод Симпсона.exe и rar-архива содержащего все компоненты программы написанных на языке программирования – Delphi 7.0. 1. Запуск программы осуществляется путем открытия файла Метод Симпсона .exe. Рис 1. 2. Ввод значений производится следующим образом: Рис 2. Ввод функции f(x) – в данное ...



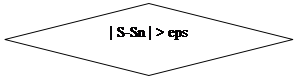

0 комментариев