Содержание. 1
Используемая литература. 1
Метод Ньютона (касательных). 2
Описание. 2
Блок-схема алгоритма. 3
Листинг программы.. 4
Результаты работы программы.. 6
Пример №1. 6
Пример №2. 6
Пример №3. 7
Метод итераций. 8
Блок-схема алгоритма. 8
Листинг программы.. 9
Результаты работы программы.. 11
Пример №1. 11
Пример №2. 11
Пример №3. 12
Используемая литература1. http://www.kyshtym.net.ru/rww/ Учимся программировать на С++
2. http://www.sprin.ru/soft.php Решение линейных уравнений методом Ньютона (касательных)
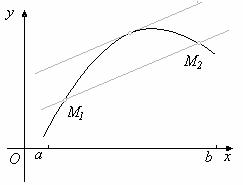
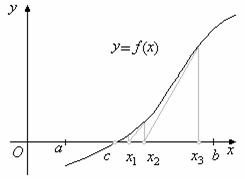
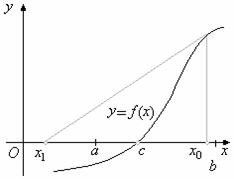
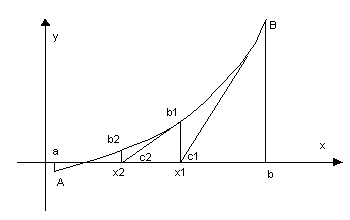
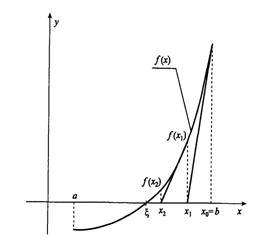
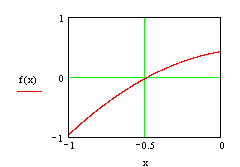
В рамках метода Ньютона предполагается, что функция дифференцируема. Согласно этому методу строится линейная аппроксимация функции в начальной точке, а точка, в которой аппроксимирующая линейная функция обращается в нуль, принимается в качестве следующего приближения.
Итерационый процесс схождения к корню реализуется формулой:
xn+1=xn-f(xn)/f '(xn). Вычисления продолжаются пока соблюдается условие
|xn+1-xn |>=eps.
В зависимости от выбора начальной точки и вида функции алгоритм по методу Ньютона может как сходиться к корню уравнения, так и расходиться.
Ниже приведена блок-схема алгоритма и листинг программы, реализующей данный алгоритм на языке С++. Также привожу текст, которая выдает данная программа при решении исходного уравнения.
Блок-схема алгоритма
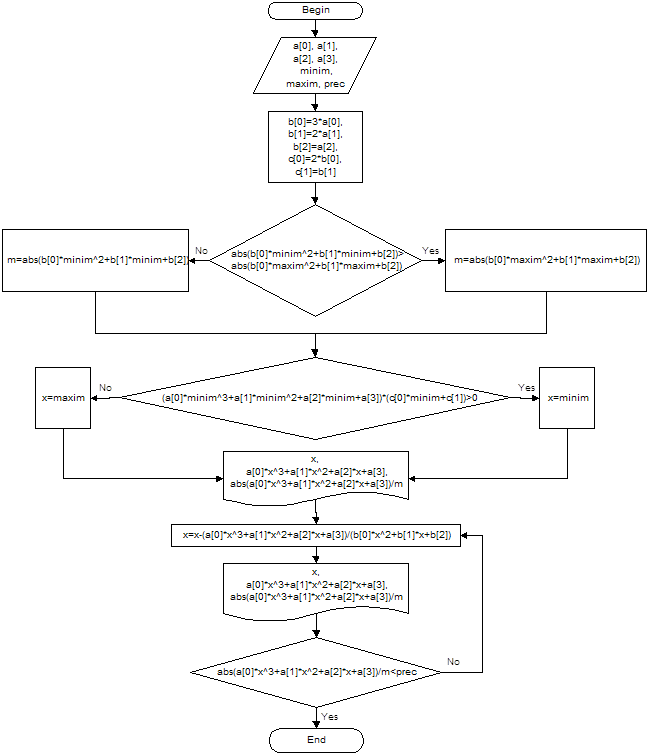
Листинг программы
//метод Ньютона для решения кубических уравнений
#include<math.h>
#include<iostream.h>
double a[4]={0},
b[3]={0},
c[2]={0},
prec=0.00000;
double minim=0, maxim=0;
void Hello(void);
void Input();
void Derivative();
void Calculation();
double Calc_Fun(double);
double Calc_First(double);
double Calc_Second(double);
main(void)
{
Hello();
Input();
Derivative();
Calculation();
return 0;
}
void Hello(void)
{
cout<<"Программа для решения кубических уравнений методом касательных (метод Ньютона).\n\n";
}
void Input()
{
cout<<"Кубическое уравнение имеет вид"<<endl
<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;
for (int i=0;i<4;i++)
{
cout<<"Введите значение коэффициента a["<<i+1<<"] : ";
cin>>a[i];
}
cout<<endl<<"Необходимо указать интервал поиска решения."<<endl
<<"Введите нижнюю границу поиска : ";
cin>>minim;
cout<<"Введите верхнюю границу поиска : ";
cin>>maxim;
while(minim==maxim||minim>maxim)
{
cout<<"\nНижняя граница должна быть меньше верхней и не может быть ей равна."<<endl
<<"Повторите ввод нижней границы : ";
cin>>minim;
cout<<"Повторите ввод верхней границы : ";
cin>>maxim;
}
cout<<"Введите допустимую погрешность : ";
cin>>prec;
}
void Derivative()
{
b[0]=a[0]*3;
b[1]=a[1]*2;
b[2]=a[2];
c[0]=b[0]*2;
c[1]=b[1];
cout<<"\n\n\n"
<<"Исходное уравнение имеет вид : \n\n"
<<a[0]<<"x^3+("<<a[1]<<")x^2+("<<a[2]<<")x+("<<a[3]<<")=0\n\n"
<<"Первая производная имеет вид : \n\n"
<<"f'(x)="<<b[0]<<"x^2+("<<b[1]<<")x+("<<b[2]<<")\n\n"
<<"Вторая производная имеет вид : \n\n"
<<"f''(x)="<<c[0]<<"x+("<<c[1]<<")\n\n";
}
void Calculation()
{
double x=0, m=0;
cout<<"-------------------------------------------------"<<endl
<<"| Xn | f(Xn) | |f(Xn)|/m |"<<endl
<<"-------------------------------------------------"<<endl;
if (abs(Calc_Fun(minim))*abs(Calc_Second(minim))>0) x=minim;
else x=maxim;
if (Calc_First(minim)>Calc_First(maxim)) m=abs(Calc_First(maxim));
else m=abs(Calc_First(minim));
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<(fabs(Calc_Fun(x))/m);
cout<<"|\n";
while((fabs(Calc_Fun(x))/m)>prec)
{
x=(x-(Calc_Fun(x)/Calc_First(x)));
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<fabs(Calc_Fun(x))/m;
cout<<"|\n";
}
cout<<"-------------------------------------------------";
}
double Calc_Fun(double x)
{
return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);
}
double Calc_First(double x)
{
return (b[0]*x*x+b[1]*x+b[2]);
}
double Calc_Second(double x)
{
return (c[0]*x+c[1]);
}
Результаты работы программы Пример №1
![]()
Программа для решения кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решения.
Введите нижнюю границу поиска : -4
Введите верхнюю границу поиска : -3
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
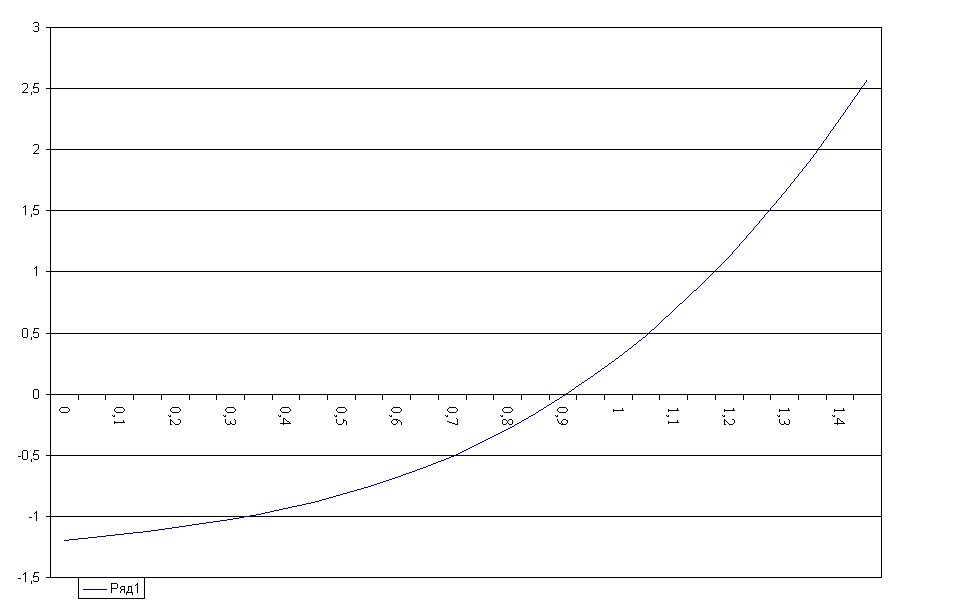
1x^3+(-6)x^2+(-9)x+(58)=0
Первая производная имеет вид :
f'(x)=3x^2+(-12)x+(-9)
Вторая производная имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| -4| -66| 1.222222222|
| -3.24137931| -9.922506048| 0.183750112|
| -3.079817529| -0.40621762| 0.007522548518|
| -3.07261683|-0.000789793230|1.462580056e-05|
-------------------------------------------------
Пример №2![]()
Программа для решения кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решения.
Введите нижнюю границу поиска : 3
Введите верхнюю границу поиска : 4
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
Первая производная имеет вид :
f'(x)=3x^2+(-12)x+(-9)
Вторая производная имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| 3| 4| 0.4444444444|
| 3.222222222| 0.159122085| 0.01768023167|
| 3.231855174| 0.000341137633|3.790418145e-05|
-------------------------------------------------
Пример №3![]()
Программа для решения кубических уравнений методом касательных (метод Ньютона).
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решения.
Введите нижнюю границу поиска : 5
Введите верхнюю границу поиска : 6
Введите допустимую погрешность : 0.00005
Исходное уравнение имеет вид :
1x^3+(-6)x^2+(-9)x+(58)=0
Первая производная имеет вид :
f'(x)=3x^2+(-12)x+(-9)
Вторая производная имеет вид :
f''(x)=6x+(-12)
-------------------------------------------------
| Xn | f(Xn) | |f(Xn)|/m |
-------------------------------------------------
| 6| 4| 0.6666666667|
| 5.851851852| 0.2601229487| 0.04335382479|
| 5.840787634| 0.001413241032| 0.000235540172|
| 5.840726862|4.255405933e-08|7.092343222e-09|
-------------------------------------------------
Метод итераций. Блок-схема алгоритма
Блок-схема решения и листинг программы, реализующей этот алгоритм на языке программирования С++.
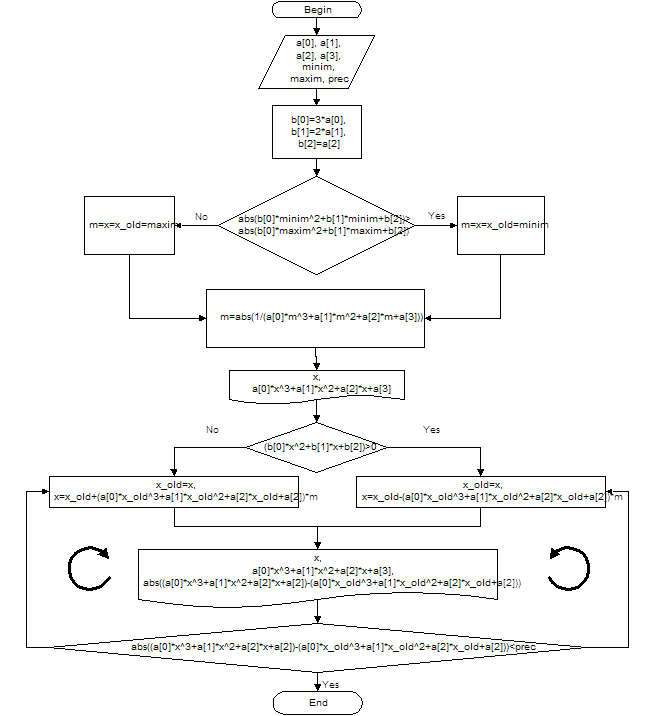
Листинг программы
//метод итераций для решения кубических уравнений
#include<math.h>
#include<iostream.h>
double a[4]={0},
b[3]={0},
prec=0.00000;
double minim=0, maxim=0;
void Hello(void);
void Input();
void Derivative();
void Calculation();
double Calc_Fun(double);
double Calc_First(double);
main(void)
{
Hello();
Input();
Derivative();
Calculation();
return 0;
}
void Hello(void)
{
cout<<"Программа для решения кубических уравнений методом итераций.\n\n";
}
void Input()
{
cout<<"Кубическое уравнение имеет вид"<<endl
<<"a1*x^3+a2*x^2+a3*x+a4=0"<<endl<<endl;
for (int i=0;i<4;i++)
{
cout<<"Введите значение коэффициента a["<<i+1<<"] : ";
cin>>a[i];
}
cout<<endl<<"Необходимо указать интервал поиска решения."<<endl
<<"Введите нижнюю границу поиска : ";
cin>>minim;
cout<<"Введите верхнюю границу поиска : ";
cin>>maxim;
while(minim==maxim||minim>maxim)
{
cout<<"\nНижняя граница должна быть меньше верхней и не может быть ей
равна." <<endl
<<"Повторите ввод нижней границы : ";
cin>>minim;
cout<<"Повторите ввод верхней границы : ";
cin>>maxim;
}
cout<<"Введите допустимую погрешность : ";
cin>>prec;
}
void Derivative()
{
b[0]=a[0]*3;
b[1]=a[1]*2;
b[2]=a[2];
}
void Calculation()
{
double x=0, x_old=0, m=0;
cout<<"-------------------------------------------------"<<endl
<<"| Xn | f(Xn) | X(n+1)-Xn |"<<endl
<<"-------------------------------------------------"<<endl;
if(fabs(Calc_First(minim))>fabs(Calc_First(maxim))) m=x=x_old=minim;
else m=x=x_old=maxim;
m=fabs(1/Calc_First(m));
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"| |\n";
if(Calc_First(x)>0)
{
do
{
x_old=x;
x=x_old-m*Calc_Fun(x_old);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<fabs( Calc_Fun(x) - Calc_Fun(x_old) );
cout<<"|\n";
}
while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);
}
else
{
do
{
x_old=x;
x=x_old+m*Calc_Fun(x_old);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<x;
cout<<"|";
cout.width(15);cout.precision(10);
cout<<Calc_Fun(x);
cout<<"|";
cout.width(15);cout.precision(10);
cout<<fabs( Calc_Fun(x) - Calc_Fun(x_old) );
cout<<"|\n";
}
while(( fabs( Calc_Fun(x) - Calc_Fun(x_old) ) )>prec);
}
cout<<"-------------------------------------------------";
}
double Calc_Fun(double x)
{
return (a[0]*x*x*x+a[1]*x*x+a[2]*x+a[3]);
}
double Calc_First(double x)
{
return (b[0]*x*x+b[1]*x+b[2]);
}
![]()
Результаты работы программы Пример №1
Программа для решения кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решения.
Введите нижнюю границу поиска : -4
Введите верхнюю границу поиска : -3
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| -4| -66| |
| -3.24137931| -9.922506048| 56.07749395|
| -3.127327517| -3.12093462| 6.801571427|
| -3.091454705| -1.064778438| 2.056156183|
| -3.079215872| -0.372281515| 0.6924969227|
| -3.074936774| -0.131239433| 0.241042082|
| -3.073428275| -0.04639844126| 0.08484099175|
| -3.07289496| -0.01642029825| 0.02997814301|
| -3.072706221|-0.005813178631| 0.01060711962|
| -3.072639403|-0.002058264249| 0.003754914382|
| -3.072615744|-0.000728799396| 0.001329464852|
| -3.072607367|-0.000258060628|0.0004707387678|
| -3.072604401|-9.137721784e-0|0.0001666834108|
| -3.072603351|-3.235601088e-0|5.902120696e-05|
| -3.072602979|-1.145703711e-0|2.089897377e-05|
-------------------------------------------------
Пример №2![]() Программа для решения кубических уравнений методом итераций.
Программа для решения кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решения.
Введите нижнюю границу поиска : 3
Введите верхнюю границу поиска : 4
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| 3| 4| |
| 3.222222222| 0.159122085| 3.840877915|
| 3.231062338| 0.01338370012| 0.1457383849|
| 3.231805877| 0.001151957391| 0.01223174272|
| 3.231869875|9.934183961e-05| 0.001052615552|
| 3.231875394|8.568402322e-06|9.077343728e-05|
| 3.23187587|7.390497921e-07| 7.82935253e-06|
-------------------------------------------------
Пример №3![]()
Программа для решения кубических уравнений методом итераций.
Кубическое уравнение имеет вид
a1*x^3+a2*x^2+a3*x+a4=0
Введите значение коэффициента a[1] : 1
Введите значение коэффициента a[2] : -6
Введите значение коэффициента a[3] : -9
Введите значение коэффициента a[4] : 58
Необходимо указать интервал поиска решения.
Введите нижнюю границу поиска : 5
Введите верхнюю границу поиска : 6
Введите допустимую погрешность : 0.00005
-------------------------------------------------
| Xn | f(Xn) | X(n+1)-Xn |
-------------------------------------------------
| 6| 4| |
| 5.851851852| 0.2601229487| 3.739877051|
| 5.842217669| 0.0346921878| 0.2254307609|
| 5.840932773| 0.004788677115| 0.02990351069|
| 5.840755414|0.0006639855431| 0.004124691572|
| 5.840730822|9.212373716e-05|0.0005718618059|
| 5.84072741|1.278267885e-05|7.934105832e-05|
| 5.840726937|1.773688694e-06|1.100899016e-05|
-------------------------------------------------
![]()
МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ ТАТАРСТАН
АЛЬМЕТЬЕВСКИЙ НЕФТЯНОЙ ИНСТИТУТ
Кафедра информатики
Курсовая работа
На тему: метод касательных (метод Ньютона)
Работу выполнил студент гр. 52-61
Низамова Г.Н.
Проверил: Борганова Э.М.
Альметьевск 2003 г.
Похожие работы
... - в методе Ньютона наблюдается ускорение сходимости процесса приближений. 5. Метод касательных (метод Ньютона) Метод касательных, связанный с именем И. Ньютона, является одним из наиболее эффективных численных методов решения уравнений. Идея метода очень проста. Возьмём производную точку x0 и запишем в ней уравнение касательной к графику функции f(x): y=f(x0)+ f ¢(x) (x-x0) (1.5) Графики ...
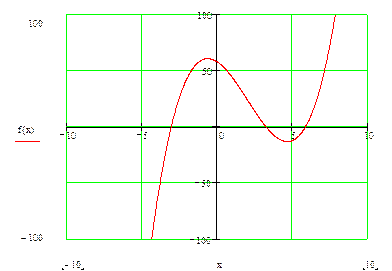
... интервал, на котором будем находить решение. Для отделения корней существует несколько способов. Наиболее популярные из них – графический и аналитический. В литературе рассматриваются эти способы по отдельности. По заданию курсовой работы требуется отделить корни каждым из этих способов. Рискну нарушить это требование, и объединить эти два способа в один. То есть исследовать функцию аналитически ...
... : в работе инженера. СОДЕРЖАНИЕ стр. ВВЕДЕНИЕ........................................ 5 1. Краткое описание сущности метода касательных ( метода секущих Ньютона).................... 7 2. Решение нелинейного уравнения аналитически .. 9 3. Блок схема программы ........................ 11 4. Программа на языке ...
... 35437 x4=0.58554 5 x1=1.3179137 x2=-1.59467 x3=0.35371 x4=0.58462 6 x1=1.3181515 x2=-1.59506 x3=0.35455 x4=0.58557 5. Сравнительный анализ различных методов численного дифференцирования и интегрирования 5.1 Методы численного дифференцирования 5.1.1 Описание метода Предположим, что в окрестности точки xiфункция F (x) дифференцируема достаточное число раз. ...
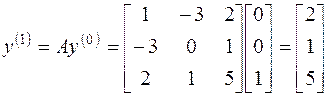
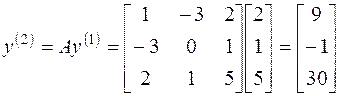
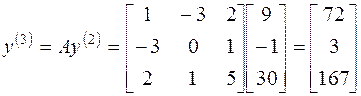
0 комментариев