Навигация
Курсовая работа по численным методам
21954
знака
7
таблиц
10
изображений
1. Методом Крылова развернуть характеристический определитель матрицы А=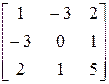
. Исходную систему линейных уравнений решить методом Жордана-Гаусса.
Решение. Метод Крылова основан на свойстве квадратной матрицы обращать в нуль свой характеристический многочлен.
Согласно теореме Гамильтона-Кали, всякая квадратная матрица является корнем своего характеристического многочлена и, следовательно, обращает его в нуль.
Пусть
– (1)
характеристический многочлен.
Заменяя в выражении (1) величину 
на 
, получим
. (2)
Возьмем произвольный ненулевой вектор
. (3)
Умножим обе части выражения (2) на 
:
(4)
Положим
, (5)
т.е.
(6)
Учитывая (5), выражение (4) запишем в виде
, (7)
или в виде
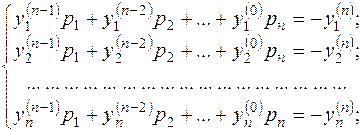
Решаем систему (7). Если эта система имеет единственное решение, то ее корни 
являются коэффициентами характеристического многочлена (1).
Если известны коэффициенты и корни 
характеристического многочлена, то метод Крылова дает возможность найти соответствующие собственные векторы по следующей формуле:
(8)
Здесь 
– векторы, использованные при нахождении коэффициентов методом Крылова, а коэффициенты 
определяются по схеме Горнера
(9)
Используя все выше сказанное, развернем характеристический определитель матрицы А=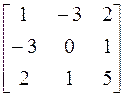
методом Крылова.
Выберем в качестве начального следующий вектор:
, 
Вычислим
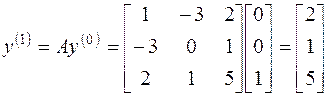
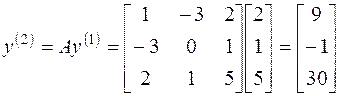
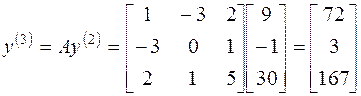
Составим матричное уравнение
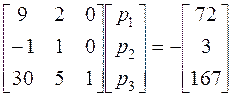, или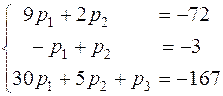 
Полученную систему уравнений решим методом Жордана-Гаусса.
|
|
|
|
|
|
| |
| 1 | 9 | 2 | 0 | -72 | -61 | -61 |
| -1 | 1 | 0 | -3 | -3 | -3 | |
| 30 | 5 | 1 | -167 | -131 | -131 | |
| 2 | 1 | 2/9 | 0 | -8 | -61/9 | -61/9 |
| 0 | 11/9 | 0 | -11 | -88/9 | -88/9 | |
| 0 | -15/9 | 1 | 657/9 | 651/9 | 651/9 | |
| 3 | 1 | 0 | 0 | -6 | -5 | -5 |
| 0 | 1 | 0 | -9 | -8 | -8 | |
| 0 | 0 | 1 | 58 | 59 | 59 | |
| 4 | 1 | 0 | 0 | |||
| 0 | 1 | 0 | ||||
| 0 | 0 | 1 |
Исходя из результатов таблицы, имеем 
.
Таким образом характеристическое уравнение матрицы имеет вид
2. Для определения собственных чисел матрицы необходимо решить полученное характеристическое уравнение третьей степени
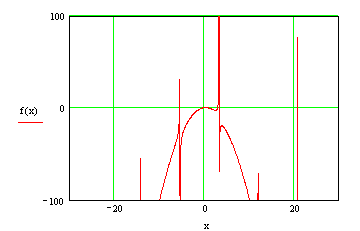
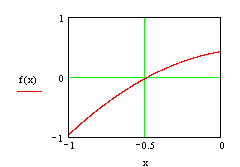
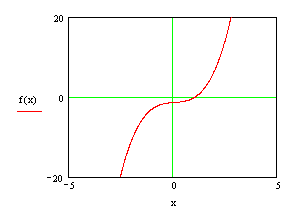
Данное кубическое уравнение невозможно решить стандартными средствами. Воспользуемся для этой цели числовыми методами, а точнее методами приближенного вычисления.
Похожие работы
... затрачивается большой объем памяти для хранения промежуточных данных (u,v,p,…). Метод Рунге скорее удобен для вычисления вручную, но менее актуален в программировании. Если говорить о нахождении более оптимального метода расчета коэффициентов Фурье на ЭВМ, то таким является вышеописанное быстрое преобразование Фурье. Он позволяет сократить количество операций до . В сравнении с вышеописанными ...
... точке приближенного решения, т. е. Последовательные приближения (4) строятся по формулам: , (9) где – начальное приближение к точному решению . 4.5 Метод Зейделя на основе линеаризованного уравнения Итерационная формула для построения приближенного решения нелинейного уравнения (2) на основе линеаризованного уравнения (7) имеет вид: 4.6 Метод наискорейшего спуска Методы ...
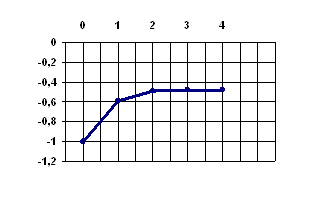
... 35437 x4=0.58554 5 x1=1.3179137 x2=-1.59467 x3=0.35371 x4=0.58462 6 x1=1.3181515 x2=-1.59506 x3=0.35455 x4=0.58557 5. Сравнительный анализ различных методов численного дифференцирования и интегрирования 5.1 Методы численного дифференцирования 5.1.1 Описание метода Предположим, что в окрестности точки xiфункция F (x) дифференцируема достаточное число раз. ...
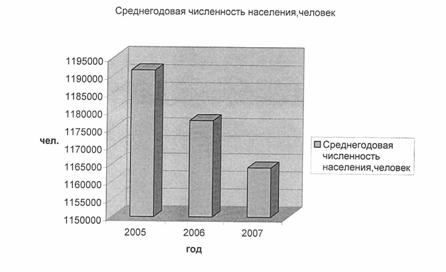
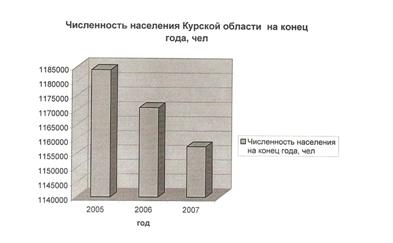
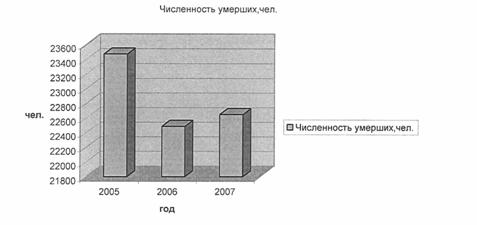
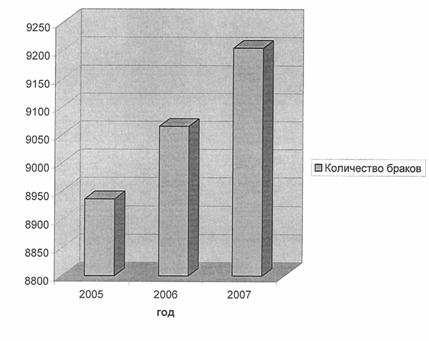
... производства, выполненных работ и услуг собственными силами по добыче полезных ископаемых в 2006 г. область занимает 22 место в России, по обрабатывающим производствам - 51, по производству и распределению электроэнергии, газа и воды - 28. 2.2 Статистическое изучение численности населения области Для характеристики численности населения представим имеющиеся данные о численности населения. ...
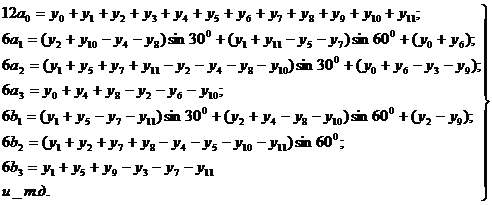
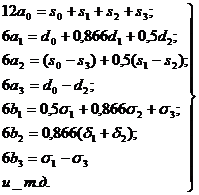
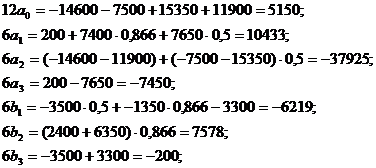
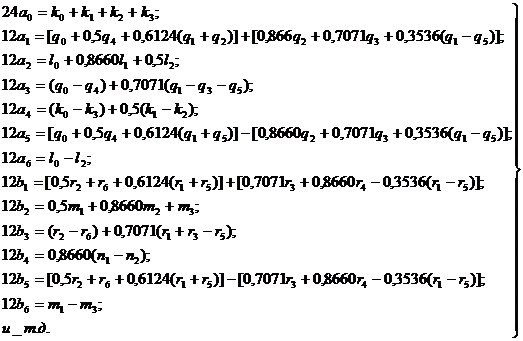
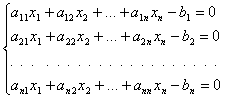
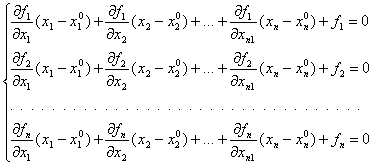
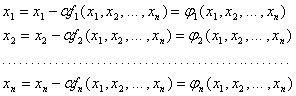
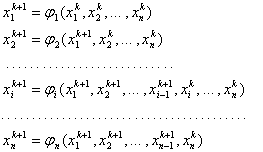
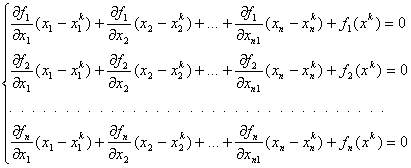
0 комментариев