Навигация
Уравнение переходной функции получаем путем проведения обратного преобразования по Лапласу (см. табл.1 задание 4)
6. Уравнение переходной функции получаем путем проведения обратного преобразования по Лапласу (см. табл.1 задание 4).
x(t)=10-11.33*e-2t+1.877*e+j111°*e(-3+4j)*t+1.877*e-j111°*e(-3-4j)*t=
=10-11.33*e-2t+1.877*(e+j*(111°+4t)+e-j*(111°+4t))*e-3t.
Выражение в скобках преобразуем согласно формуле Эйлера.
(e+ja+e-ja)=2*cosa
x(t)=10-11.33*e-2t+1.877*e-3t*2*cos(4t+111°)=
=10-11.33*e-2t+3.75*e-3t*cos(4t-1.204).
Примечание. cos(111°)= -cos(180°-111°)= -cos(-69°)= -cos(-1.204), где 1.204 угол в радианах от j=69°.
Проверим правильность вычисления коэффициентов c.
При t=0 значение x(t=0)=0, т.к. начальные условия нулевые.
x(t)=10-11.33*1+3.75*1*cos(-1.2)=-1.33+3.75*0.3583=-1.33+1.343=0.
Условия выполняются в пределах точности вычисления.
6.Уравнение переходной функции.
x(t)=10-11.33*e-2t+3.75*e-3t*cos(4t-1.204).
ПРИМЕР 8. Определить уравнение весовой функции по ПФ примера №7:
W(p)=
РЕШЕНИЕ.
1. Определяем изображение по Лапласу регулируемого параметра, учитывая, что U(p)=1.
x(p)=
2. Определяем корни характеристического уравнения.
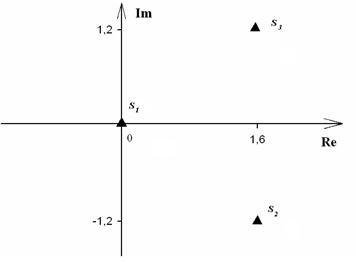
p1= -2 p2,3= -3±j4.
4. Разложим полученное изображение x(p) на простые дроби.
x(p)=
5. Определяем коэффициенты разложения c.
c1(p1=-2)=
c2(p2=-3+j4)=
c3(p3)=-3-j4=7.45*e+j*137°54’.
5. Представим изображение по Лапласу регулируемого параметра в виде простых дробей с учетом полученных значений c1,c2,c3.
x(p)=
6. Уравнение весовой функции получаем путем проведения обратного преобразования по Лапласу.
x(t)=22.66*e-2t+7.45*e-j*137°54’*e(-3-j4)*t+7.45*ej*137°94’*e(3+j4)*t=
=22.66*e-2t+7.45+7.45*e-3t*(ej*(-137°54’+4t)+e-j*(-137°54’+4t))=
=22.66*e-2t+14.9*e-3t*cos(4t-2.4),
где 2.4 угол в радианах от j=-137°54’.
2. ИСХОДНЫЕ ДАННЫЕ ДЛЯ ВЫПОЛНЕНИЯ ЗАДАНИЯ.
Определить уравнение переходного процесса по заданной П.Ф.
W(p)=
Значения коэффициентов k и Тi показано в таблице 1.
Таблица 1 - Значение коэффициентов k и Т для задания 5.
| № варианта | Вид воздействия | k | T1 | T2 | T3 | T4 |
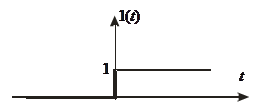
| 1 | 1(t) | 2 | 0.25 | 0.005 | 0.07 | 0.325 |
| 2 | 1(t) | 4 | 0.3 | 0.00625 | 0.03 | 0.325 |
| 3 | 1(t) | 5 | 0.16 | 0.0 | 0.05 | 0.4 |
| 4 | 1(t) | 3 | 0.12 | 0.0077 | 0.107 | 0.4 |
| 5 | 1(t) | 10 | 0.24 | 0.015 | 0.21 | 0.8 |
| 6 | 1’(t) | 6 | 0.15 | 0.03 | 0.4 | 1.2 |
| 7 | 1’(t) | 8 | 0.2 | 0.002 | 0.04 | 0.18 |
| 8 | 1’(t) | 4 | 0.08 | 0.012 | 0.16 | 0.62 |
| 9 | 1’(t) | 4 | 0.72 | 0.018 | 0.18 | 2.2 |
| 10 | 1’(t) | 2 | 0.32 | 0.01 | 0.06 | 0.92 |
3. ПОРЯДОК ВЫПОЛНЕНИЯ ЗАДАНИЯ
1. Записать передаточную функцию, вид управляющего воздействия согласно варианту задания.
2. Определяется регулируемый параметр в изображении по Лапласу.
3. Определить корни.
4. Разложить изображение по Лапласу регулируемой величины на простейшие дроби.
5. Определить коэффициенты разложения C.
6. Преобразовать простейшие дроби с комплексными корнями к виду, удобному для проведения обратного преобразования по Лапласу по первому и второму варианту.
7. Получить уравнение переходного процесса при нулевых начальных условиях.
4. СОДЕРЖЕНИЕ ОТЧЕТА ПО ВЫПОЛНЕНОЙ РАБОТЕ.
В отчете должно быть показано:
1. Заданная ПФ.
2. Вид воздействия.
3. Начальные условия.
4. Изображение по Лапласу регулируемого параметра.
5. Определение корней.
6. Представление регулируемого параметра через простые дроби.
7. Вычисление коэффициентов разложения.
8. Уравнение переходного процесса.
5. КОНТРОЛЬНЫЕ ВОПРОСЫ
1. Как выглядит изображение по Лапласу регулируемого параметра при импульсном воздействии, если u(t)=4.
2. Как выглядит изображение по Лапласу регулируемого параметра при скачкообразном воздействии, если u(t)=4(t).
3. Как определяется изображение по Лапласу регулируемого параметра, если u’(t)=4t.
4. Какой вид имеет переходный процесс при скачкообразном воздействии, если корни вещественные отрицательные.
5. Какой вид имеет переходный процесс, если корни чисто мнимые.
6. Какой вид имеет переходный процесс, если корни комплексные.
7. Какой вид имеет переходный процесс, если корни вещественные положительные.
8. Как в первом приближении можно определить корни характеристического уравнения.
9. Как во втором приближении можно определить корни характеристического уравнения.
10. Что делать, если при определении корней процесс расходится.
11. Как определяются коэффициенты разложения, если корни вещественные и разные.
12. Как определяются коэффициенты разложения, если есть один корень равный нулю.
13. Как определяются коэффициенты разложения, если корни комплексные.
14. Как проверить правильность получения коэффициентов разложения.
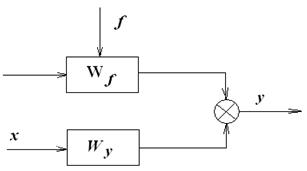
15. Как получить уравнение переходного процесса при одновременном воздействии управляющего и возмущающего сигналов.
Похожие работы
... , феноло- и мочевиноформальдегидных смол, а также применяют в производстве пластмасс, резиновых изделий, бумаги, линолеума, искусственных волокон и немного в парфюмерии. Цель дипломного проекта - автоматизация технологического процесса получения диоксида титана. 3. Технология производства. 3.1 Описание технологического процесса. Очищенный в отделении ректификации тетрахлорид титана (ОТТ) насосом ...
... можно записать: . (4) Для определения установившегося значения можно полагать, что воздействие началось в момент и для расчета использовать выражение: . Использование частотных передаточных функций Частотная передаточная функция (комплексный коэффициент передачи) определяет реакцию системы на гармоническое входное воздействие и используется для анализа следящих систем. Ее можно найти, ...
... равна: . Для процесса с 20 % перерегулированием ПИД-регулятора, его настройки: ; ; . Практическая работа № 4 Дана одноконтурная АСР. Требуется определить: · передаточные функции регулятора и объекта управления, · передаточную функцию разомкнутой системы W∞(s), · характеристическое выражение замкнутой системы (ХВЗС), · передаточные функции замкнутой системы Фз(s) – по ...
... АСР. Данная схема детализируется для расчета замкнутой АСР и приводится к виду X0 Wp(p) Рис. 7. Структурная схема замкнутой автоматической системы управления, состоящей из объекта и регулятора В качестве выходной величины системы ...

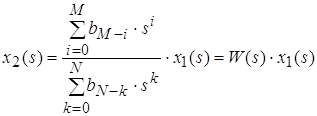
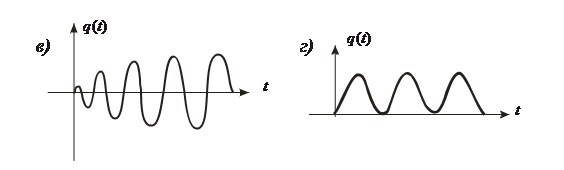
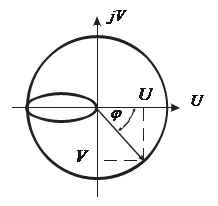
0 комментариев