Навигация
Различные порождающие правила имеют разные правые части
2. Различные порождающие правила имеют разные правые части.
Отношения =, < и > называют отношениями предшествования для символов. Отношение предшествования единственно для каждой упорядоченной пары символов. При этом между какими-либо двумя символами может и не быть отношения предшествования - это значит, что они не могут находиться рядом ни в одном элементе разбора синтаксически правильной цепочки. Отношения предшествования зависят от порядка, в котором стоят символы, и в этом смысле их нельзя путать со знаками математических операций - например, если Si > Sj, то не обязательно, что Sj < Si (поэтому знаки предшествования иногда помечают специальной точкой: =× , <× , × >)
Метод предшествования основан на том факте, что отношения предшествования между двумя соседними символами распознаваемой строки соответствуют трем следующим вариантам:
· Si < Si+1, если символ Si+1 - крайний левый символ некоторой основы;
· Si > Si+1 , если символ Si - крайний правый символ некоторой основы;
· Si = Si+1 , если символы Si и Si+1 принадлежат одной основе.
Исходя из этих соотношений выполняется разбор строки для грамматики предшествования.
На основании отношений предшествования строят матрицу предшествования грамматики. Строки матрицы предшествования помечаются первыми символами, столбцы - вторыми символами отношений предшествования, а в клетки матрицы на пересечении соответствующих столбца и строки помещаются знаки отношений. При этом пустые клетки матрицы говорят о том, что между данными символами нет ни одного отношения предшествования.
Матрицу предшествования грамматики можно построить, опираясь непосредственно на определения отношений предшествования, но удобнее воспользоваться двумя дополнительными множествами - множеством крайних левых и множеством крайних правых символов относительно нетерминалов грамматики. Эти множества определяются следующим образом:
· L(U) = {T | $ UÞ *Tz}, U,TÎ V, zÎ V* - множество крайних левых символов относительно нетерминального символа U (цепочка z может быть и пустой цепочкой);
· R(U) = {T | $ UÞ *zT}, U,TÎ V, zÎ V* - множество крайних правых символов относительно нетерминального символа U.
Тогда отношения предшествования можно определить так:
· Si = Sj (" Si,SjÎV), если $ правило U® xSiSjy Î P, где UÎ VN, x,yÎ V*;
· Si < Sj (" Si,SjÎV), если $ правило U® xSiDy Î P и SjÎL(D), где U,DÎ VN, x,yÎ V*;
· Si > Sj (" Si,SjÎV) , если $ правило U® xCSjy Î P и SiÎR(C) или $ правило U® xCDy Î P и SiÎR(C), SjÎL(D), где U,C,DÎ VN, x,yÎ V*.
Такое определение отношений удобнее на практике, так как не требует построения выводов, а множества L(U) и R(U) могут быть построены для каждого нетерминального символа UÎ VN по очень простому алгоритму:
Шаг 1. Для каждого нетерминального символа U ищем все правила, содержащие U в левой части. Во множество L(U) включаем самый левый символ из правой части правил, а во множество R(U) - самый крайний символ правой части. Переходи к шагу 2.
Шаг 2. Для каждого нетерминального символа U: если множество L(U) содержит нетерминальные символы грамматики U’,U”,..., то его надо дополнить символами, входящими в соответствующие множества L(U’), L(U”), ... и не входящими в L(U). Ту же операцию надо выполнить для R(U).
Шаг 3. Если на предыдущем шаге хотя бы одно множество L(U) или R(U) для некоторого символа грамматики изменилось, то надо вернуться к шагу 2, иначе построение закончено.
После построения множеств L(U) и R(U) по правилам грамматики создается матрица предшествования. Матрицу предшествования дополняют символами ^ н и ^ к (начало и конец цепочки). Для них определены следующие отношения предшествования:
^ н < a, " aÎ V, если $ SÞ *ax, где SÎ VN, xÎ V* или (с другой стороны) если aÎ L(S);
^ к > a, " aÎ V, если $ SÞ *xa, где SÎ VN, xÎ V* или (с другой стороны) если aÎ R(S).
3.2 Грамматики операторного предшествованияГрамматикой операторного предшествования называется приведенная КС-грамматика без l -правил (e-правил), в которой правые части продукций не содержат смежных нетерминальных символов. Для грамматики операторного предшествования отношения предшествования можно задать на множестве терминальных символов (включая символы ^ н и ^ к).
Отношения предшествования для грамматики операторного предшествования G(VN,VT,P,S) задаются следующим образом:
· a = b, если и только если существует правило U® xaby Î P или правило U® xaCby, где a,bÎ VT, U,CÎ VN, x,yÎ V*;
· a < b, если и только если существует правило U® xaCy Î P и вывод CÞ *bz или вывод CÞ *Dbz, где a,bÎ VT, U,C,DÎ VN, x,y,zÎ V*;
· a > b, если и только если существует правило U® xCby Î P и вывод CÞ *za или вывод CÞ *zaD, где a,bÎ VT, U,C,DÎ VN, x,y,zÎ V*.
В грамматике операторного предшествования различные порождающие правила имеют разные правые части. Для грамматики операторного предшествования тоже строится матрица предшествования, но она содержит только терминальные символы грамматики.
Для построения этой матрицы удобно ввести множества крайних левых и крайних правых терминальных символов относительно нетерминального символа U - Lt(U) или Rt(U):
· Lt(U) = {t | $ UÞ *tz или $ UÞ *Ctz}, где tÎ VT, U,CÎ VN, zÎ V*;
· Rt(U) = {t | $ UÞ *zt или $ UÞ *ztC }, где tÎ VT, U,CÎ VN, zÎ V*.
Тогда определения отношений операторного предшествования будут выглядеть так:
· a = b, если $ правило U® xaby Î P или правило U® xaCby, где a,bÎ VT, U,CÎ VN, x,yÎ V*;
· a < b, если $ правило U® xaCy Î P и bÎ Lt(C), где a,bÎ VT, U,CÎ VN, x,yÎ V*;
· a > b, если $ правило U® xCby Î P и aÎ Rt(C), где a,bÎ VT, U,CÎ VN, x,yÎ V*.
В данных определениях цепочки символов x,y,z могут быть и пустыми цепочками.
Для нахождения множеств Lt(U) и Rt(U) используется следующий алгоритм:
Шаг 1. Для каждого нетерминального символа грамматики U строятся множества L(U) и R(U).
Шаг 2. Для каждого нетерминального символа грамматики U ищутся правила вида U® tz и U® Ctz, где tÎ VT, CÎ VN, zÎ V*; терминальные символы t включаются во множество Lt(U). Аналогично для множества Rt(U) ищутся правила вида U® zt и U® ztC.
Шаг 3. Просматривается множество L(U), в которое входят символы U’,U”,... Множество Lt(U) дополняется символами, входящими в Lt(U’), Lt(U”), ... и не входящими в Lt(U). Аналогичная операция выполняется и для множества Rt(U) на основе множества R(U).
Для практического использования матрицу предшествования дополняют символами ^ н и ^ к (начало и конец цепочки). Для них определены следующие отношения предшествования:
^ н < a, " aÎ VT, если $ SÞ *ax или $ SÞ *Cax, где S,CÎ VN, xÎ V* или если aÎ Lt(S);
^ к > a, " aÎ VT, если $ SÞ *xa или $ SÞ *xaC, где S,CÎ VN, xÎ V* или если aÎ Rt(S).
3.3 Пример построения матрицы предшествованияПостроим матрицу предшествования для грамматики операторного предшествования.
Рассмотрим в качестве примера грамматику G({S,B,T,J},{-,&,^,(,),p},P,S): (Терминалы выделены жирным шрифтом)
P: S ® -B (правило 1)
B ® T | B&T (правила 2 и 3)
T ® J | T^J (правила 4 и 5)
J ® (B) | p (правила 6 и 7)
Видно, что эта грамматика является грамматикой операторного предшествования.
Построим множества крайних левых и крайних правых символов L(U), R(U) относительно всех нетерминальных символов грамматики. Результат построения приведен в табл. 2.
На основе полученных множеств построим множества крайних левых и крайних правых терминальных символов Lt(U), Rt(U) относительно всех нетерминальных символов грамматики. Результат (второй и третий шаги построения) приведен в табл. 3.
Таблица 2.
Множества крайних правых и крайних левых символов грамматики (по шагам построения)
| Символ | Шаг 1 (начало построения) | Последний шаг (результат) | |||
| (U) | L(U) | R(U) | L(U) | R(U) | |
| J | ( p | ) p | ( p | ) p | |
| T | J T | J | J T ( p | J ) p | |
| B | T B | T | T B J ( p | T J ) p | |
| S | - | B | - | B T J ) p | |
Таблица 3.
Множества крайних правых и левых терминальных символов грамматики (по шагам построения)
| Символ | Шаг 1 (начало построения) | Последний шаг (результат) | |||
| (U) | Lt(U) | Rt(U) | Lt(U) | Rt(U) | |
| J | ( p | ) p | ( p | ) p | |
| T | ^ | ^ | ^ ( p | ^ ) p | |
| B | & | & | & ^ ( p | & ^ ) p | |
| S | - | - | - | - & ^ ) p | |
На основе этих множеств и правил грамматики G построим матрицу предшествования грамматики (табл. 4).
Таблица 4.
Матрица предшествования грамматики
| Символы | - | & | ^ | ( | ) | p | ^ к |
| - | < | < | < | < | > | ||
| & | > | < | < | > | < | > | |
| ^ | > | > | < | > | < | > | |
| ( | < | < | < | = | < | ||
| ) | > | > | > | > | |||
| P | > | > | > | > | |||
| ^ н | < |
Посмотрим, как заполняется матрица предшествования в табл. 4 на примере символа &. В правиле грамматики B ® B&T (правило 3) этот символ стоит слева от нетерминального символа T. В множество Lt(T) входят символы: ^ ( p. Ставим знак < в клетках матрицы, соответствующих этим символам, в строке для символа &. В то же время в этом же правиле символ & стоит справа от нетерминального символа B. В множество Rt(B) входят символы: & ^ ) p. Ставим знак > в клетках матрицы, соответствующим этим символам, в столбце для символа &. Больше символ & ни в каком правиле не встречается, значит заполнение матрицы для него закончено, берем следующий символ и продолжаем заполнять матрицу таким же методом.
Алгоритм разбора цепочек грамматики операторного предшествования игнорирует нетерминальные символы. Поэтому имеет смысл преобразовать исходную грамматику таким образом, чтобы оставить в ней только один нетерминальный символ. Тогда получим следующий вид правил:
P: E ® -E (правило 1)
E ® E | E&E (правила 2 и 3)
E ® E | E^E (правила 4 и 5)
E ® (E) | p (правила 6 и 7)
Это преобразование не ведет к созданию эквивалентной грамматики и выполняется только после построения всех множеств и матрицы предшествования. Само преобразование выполняется только с целью более эффективного выполнения алгоритма разбора, в который уже заложены необходимые данные о порядке применения правил при создании матрицы предшествования.
3.4 Линеаризация матрицы предшествованияДля компактного хранения матрицы предшествования часто можно использовать следующий прием. По матрице M[n][n], элементы которой принимают только три значения (< = >), попытаемся построить два целочисленных вектора f и g:
M[i][j] равно >, если f[i]>g[j]
M[i][j] равно <, если f[i]<g[j]
M[i][j] равно =, если f[i]=g[j]
Для получения этих векторов используется следующий метод: построить ориентированный граф, содержащий n вершин типа F и n вершин типа G;
- построить ребро графа F[i]->G[j], если i > j
- построить ребро графа F[i]<-G[j], если i < j
- склеить вершины F[i] и G[j], если i = j
Если полученный граф циклический, то линеаризация невозможна. Иначе положить f[i] равным длине самого длинного пути из F[i], g[i] равным длине самого длинного пути из G[i].
4. Руководство пользователяПосле запуска программы пользователю предлагается ввести КС-грамматику (ограничение при вводе: длина нетерминала не больше восьми символов). Ввод строки заканчивается нажатием клавиши Enter. Для определения в программе нетерминала используются символы ‘<’ и ‘>’ непосредственно между которыми находится нетерминал, знак или ‘|’, знак присвоить ‘:=’. Новая строка обязательно должна начинаться с нетерминала и последующим символом(и) ‘:=’.
Для начала анализа введённой КС-грамматике нужно нажать клавишу F5 или выбрать в меню пункт «Запуск» (меню вызывается нажатием F9). Перед тем как начать построение матрицы предшествования производится синтаксический анализ введенного текста.
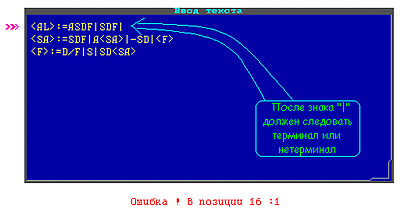 Возможные ошибки при вводе грамматики:
Возможные ошибки при вводе грамматики:
После символа ‘|’ должен обязательно следовать терминал или нетерминал.
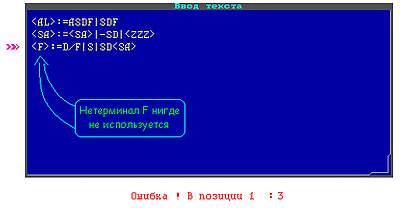
В грамматике описан нетерминал <F>, но он нигде не используется (отсутствует в правой части).
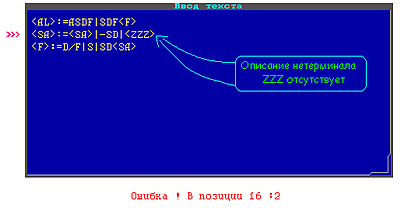
В грамматике отсутствует описание нетерминала <ZZZ> (отсутствует в правой части)
Если грамматика введена верно, то начинается построение матрицы (алгоритм описан выше). При возникновении ошибки (один или несколько (не)терминалов имеют более чем одно отношение предшествования) выводится сообщение и в соответствующую ячейку записывается символ Х.
После этого выполняется линеаризация матрицы с помощью графа: для упрощения алгоритма в матрице сначала ведется поиск отношений = при нахождении таковых выполняется склеивание соответствующих вершин. Эта операция избавляет нас от рутинных действий связанных с «перестановкой» связей. Также упрощается описание графа в программе: надобность в хранении связей отсутствует - необходимо лишь хранить количество входящих и выходящих ребер. При построении векторов граф, проверяется на цикличность (при существовании цикла выводится сообщении о невозможности построения функции предшествования).
5. Текст программы
Program KP;
Uses TpCrt,Graph,GrText,DataUnit;
Const Txt='По заданной КС-грамматике построить отношение простого'+
' или операторного предшествования и функцию предшествования,'+
' используя граф линеаризации и алгоритм пересчета с визуализацией'+
' шагов построения графа';
Errors : array [0..10] of String[34] ={ошибки}
(' КС-грамматика синтаксически верна',{0}
' Ожидается ~"<"', {1}
' Ожидается ~">"', {2}
' Ожидается ~":="', {3}
' Требуется нетерминал', {4}
' Требуется терминал', {5}
' Неопределенный нетерминал', {6}
' Неиспользуемый нетерминал', {7}
' Требуется терминал или нетерминал',{8}
' Многоопределенный нетерминал', {9}
' Найдены недопустимые символы'); {10}
menu:array[1..5] of string[10]=
('Открыть','Сохранить','Запуск','Информация','Выход');
Type
notTerm=^List;
List=Record{список терминалов и нетерминалов}
Name:Str10;{терминал или нетерминал}
Next:notTerm;
End;
strBuf=array [1..800] of Char;
matrixPr=array [1..20,1..20] of 0..4;
Var i:Byte;{текущая позиция}
s:String;{текущая строка}
Len:Byte absolute s;
str_:strBuf;{общий буфер для текста}
LenStr:Integer;{всего символов в буфере}
CLine,{кол-во строк}
y:Byte;{текущая строка}
CTerm:Byte;{кол-во нетерминалов}
CTrmNotTrm:Byte;{кол-во нетерминалов и терминалов}
notTerminalS:NotTerm;{нетерминалы встречающиеся в правых частях}
notTerminalL:NotTerm;{нетерминалы в левой части}
Trm_notTrm:NotTerm;{список терминалов и нетерминалов}
LTN:NotTerm;{левые}
RTN:NotTerm;{правые}
tmp:NotTerm;{временная переменная}
matrixPrecede:matrixPr;
LenWin:Byte;{ширина окна}
{$I Dinamic.inc} {процедуры для работы с динамическими переменными}
{$I GraphPr.inc} {графический интерфейс}
{$I ServFunc.inc} {дополнительные процедуры обработки строки}
{----------------------------------------------------------------------------}
Procedure Blank;
(* пропуск управляющих символов и пробелов *)
Begin
While (i<=Len) and (S[i] = #32) do inc(i);
End;
{}
Function Let(s:Char):Boolean;
(* контроль букв *)
Begin
Let:=((s) >= 'A') and ((s) <= 'Z') or (s in RusLetters);
End;
{}
Function Dig (s:Char;Var n:Byte):Boolean;
(* контроль цифр *)
Begin
If (s >= '0') and (s <= '9') Then
Begin
n:=ord(s)-48;
Dig:=true
End
Else Dig:=false
End;
{}
Function Terminal (Var term:String):Boolean;
(* поиск терминала *)
Begin
term:='';
If i<=Len Then
While (i<=Len) and (S[i] in Digits+LatLetters+Punctuation+Service+RusLetters)
and not (s[i]='<') and not (s[i]='>') and not (s[i]='|') Do
Begin
term:=term+s[i];
inc(i);
End;
Terminal:=term > '';
End;
{}
Function notTerminal (Var term:String):Boolean;
(* поиск нетерминала *)
Var
j:word;
n:Byte;
Ex:Boolean;
Begin
Blank;
j:=i;
term:='';
Ex:=True;
If i<=Length(s) Then
If Let(S[i]) Then
Begin
While (i<=Length(s)) and Let(S[i]) or Dig(S[i],n) do
Begin
If (i-j) < 9 Then term:=term+S[i];
inc(i);
End;
If (i-j) > 8 Then
Ex:=False
Else
Blank;
End
Else
Ex:=False
Else
Ex:=False;
notTerminal:=Ex;
End;
{}
Procedure Check;
Var term:String;
Exist,Ex:Boolean;
notT:List;
k:Byte;
Label notTerminalOrTerminal,
OrS,LineS,EndS,Start,New,Gluk;
Begin
Goto Start;
New:{при возникновении ошибки}
DeleteList(NotTerminalS);
DeleteList(NotTerminalL);
DeleteList(Trm_NotTrm);
If not InputText Then Exit;
Start:{один раз}
i:=1;
y:=1;
k:=1;
CTerm:=0;
CTrmNotTrm:=0;
PosStr(1,s);{первая строка}
If s='' Then
Goto New;
LineS:{новая строка}
GotoXY(1,10);Write(s+' Длина анализ.строки ',Length(s),' '+#13#10,'y=',y,' всего строк ',Cline);
Blank;
If not (s[i]='<') Then
Begin
Error(1);
Goto New;
End
Else
Begin
inc(i);
Blank;
If not notTerminal(term) Then
Begin
Error(4);
Goto New;
End
Else
Begin{есть нетерминал}
Blank;
If not (s[i]='>') Then
Begin
Error(2);
Goto New;
End
Else{записываем нетерминал}
Begin
NotT.Name:='<'+term+'>';
If Search(NotTerminalL,NotT)>0 Then
Begin{многоопределенный}
Error(9);
Goto New;
End;
If Search(Trm_NotTrm,NotT)=0 Then
Begin
Complete(Trm_NotTrm,NotT);{в общий список теминалов&нетерминалов}
inc(CTrmNotTrm);
End;
Complete(NotTerminalL,NotT);{лев. часть}
inc(CTerm);
inc(i);
Blank;
If not (Copy(s,i,2)=':=') Then
Begin
Error(3);
Goto New;
End
Else
Begin{есть :=}
inc(i,2);
notTerminalOrTerminal:{после := обязательный терминал или нетерминал}
Blank;
If s[i]='<' Then{нетерминал}
Begin
inc(i);
Blank;
If notTerminal(term) Then
Begin{есть нетерминал}
Blank;
If s[i]='>' Then{записываем нетерминал}
Begin
NotT.Name:='<'+term+'>';
Complete(NotTerminalS,NotT);
If Search(Trm_NotTrm,NotT)=0 Then
Begin
Complete(Trm_NotTrm,NotT);{в общий список теминалов&нетерминалов}
inc(CTrmNotTrm);
End;
inc(i);
Blank;
Goto OrS;{может быть знак ИЛИ}
End
Else
Begin
Error(2);{нет >}
Goto New;
End
End
Else
Begin
Error(4);{нет нетерминала, но < есть}
Goto New;
End
End
Else{терминал}
If Terminal(term) Then{записываем терминал}
Begin
NotT.Name:=term;
If Search(Trm_NotTrm,NotT)=0 Then
Begin
Complete(Trm_NotTrm,NotT);{в общий список теминалов&нетерминалов}
inc(CTrmNotTrm);
End;
Blank;
Goto OrS;
End
Else
Begin
Error(8);{нет нетерминала или терминала}
Goto New;
End;
OrS: If i>Len Then Goto Gluk;{обходим глюк}
If s[i]='|' Then{знак ИЛИ}
Begin
inc(i);
Goto notTerminalOrTerminal
End
Else{знака ИЛИ нет}
Begin
Blank;
If i>Len Then{конец строки ?}
Gluk: If y<CLine Then{дошли до конца строки}
Begin
{следующ. стр}
inc(y);
posStr(y,s);
If s='' Then Goto EndS;
i:=1;
Goto LineS;
End
Else{конец файла}
Goto EndS
Else Goto notTerminalOrTerminal;{знака ИЛИ нет}
End;
End;
End;
End;
End;
EndS:
{проверка нетерминалов}
tmp:=NotTerminalL^.Next;{пропускаем первый}
exist:=True;
y:=2;
While (tmp<>Nil) and Exist Do
Begin
NotT:=tmp^;
Exist:=Search(NotTerminalS,NotT)>0;
tmp:=tmp^.Next;
inc(y);
End;
dec(y);
i:=1;
While (i<=y) Do
Begin{позицианируем на нужную строку}
{в s строка с ошибкой}
posStr(y,s);
inc(i);
End;
If not Exist Then{неиспользуемый нетерминал}
Begin
i:=1;
Error(7);
Goto New;
End;
{----------------}
tmp:=NotTerminalS;
exist:=True;
While (tmp<>Nil) and Exist Do
Begin
NotT:=tmp^;
Exist:=Search(NotTerminalL,NotT)>0;
tmp:=tmp^.Next;
End;
If not Exist Then{неопределенный нетерминал}
Begin
i:=1;
y:=0;
Ex:=False;
While not Ex Do
Begin{позицианируем на нужную строку}
inc(y);
PosStr(y,s);{в s строка с ошибкой}
i:=Pos(NotT.name,s);
Ex:=i>0;
End;
Error(6);
Goto New;
End;
Window(5,21,59,25);
TextColor(15);
TextBackGround(1);
WriteLN(Errors[0]);
readkey;
End;
Procedure SearchLR;
Function SearchInBlock(n:Byte;l:NotTerm;inf:List):Byte;
Var j:Byte;
Ex:Boolean;
Begin
If l<>Nil Then
Begin
j:=1;
While (l<>Nil) and (n<>j) Do
Begin
If l^.Name=#0 Then inc(j);
l:=l^.Next;
End;
Ex:=False;
While (l<>nil) and (l^.Name<>inf.Name) and Not Ex Do
Begin
inc(j);
If l^.Name=#0 Then Ex:=True;
l:=l^.next;
End;
End;
If (l=Nil) or Ex Then SearchInBlock:=0
Else SearchInBlock:=j;
End;
Procedure InsListInBlock(n:Byte; l:NotTerm;x,d:List);
Var q:NotTerm;
j:Byte;
Begin
If l=Nil Then WriteLN('Внимание! Внутренняя ошибка 03')
Else
Begin
j:=1;
While (l<>Nil) and (n<>j) Do
Begin
If l^.Name=#0 Then inc(j);
l:=l^.Next;
End;
While (l<>Nil) and (l^.Name<>x.Name) Do
l:=l^.Next;
If l<>Nil Then
Begin
new(q);
q^.Name:=d.Name;
q^.Next:=l^.Next;
l^.Next:=q;
End;
End;
End;
Procedure Add_(ListLR:NotTerm);
Var tmp,p:NotTerm;
tmp2:NotTerm;
tmpName:Str10;
y,j:Byte;
inf:List;
inf2:List;
Begin
y:=1;
tmp:=ListLR;{список с разделителями}
p:=tmp;
Repeat
{ищем нетерминал (в левых или правых)}
tmp:=p;
tmp2:=NotTerminalL;
While (tmp<>Nil) and (Pos('<',tmp^.Name)<>1) Do
Begin
If tmp^.Name=#0 Then inc(y);
tmp:=tmp^.Next;
End;
If tmp=Nil Then p:=Nil
Else If tmp^.Next<>Nil Then
p:=tmp^.Next{сохраняем позицию указатель на следующий}
Else p:=Nil;
tmpName:=tmp^.Name;
i:=1;
{ищем tmpName в правых или левых}
If tmp<>Nil Then Seek(tmpName,ListLR,tmp);
{tmp указывает на элемент с которого нужно начать добавлять}
inf2.Name:=tmpName;
While (tmp<>Nil) and (tmp^.Name<>#0) Do
Begin
inf.Name:=tmp^.Name;{!!! нужно проверить на повторяющиеся !!!}
If SearchInBlock(y,ListLR,inf)=0 Then
InsListInBlock(y,ListLR,inf2,inf);
tmp:=tmp^.Next;
End;
Until p=Nil;
End;
Var tmp:List;
term:String;
Label More,Next;
Begin
{предполагаем что грамматика не содержит ошибок}
{анализ грамматики без отслеживания ошибок}
y:=1;
i:=1;
Repeat
PosStr(y,s);
Blank;
i:=Pos('=',S)+1;{i ставим после :=}
More:Blank;
If s[i]='<' Then
Begin
inc(i);
Blank;
Terminal(term);
tmp.Name:='<'+term+'>';
If (SearchInBlock(y,LTN,tmp)=0) and (term>'') Then
Complete(LTN,tmp);{добавляем левый}
Blank;
inc(i);
End
Else
Begin
Terminal(term);
tmp.Name:=term;
If (SearchInBlock(y,LTN,tmp)=0) and (term>'') Then
Complete(LTN,tmp);{добавляем левый}
If (i-1)=Len Then {после := или после | только один терминал}
Complete(RTN,tmp);
End;
If i>Len Then Goto Next;{последний в строке был терминал}
While (i<Len) and (S[i+1]<>'|') Do inc(i);{до конца правила}
If s[i]='>' Then {последний в правиле нетерминал}
Begin
While (i>1) and (s[i]<>'<') Do dec(i);
inc(i);
Blank;
Terminal(term);{последний нетерминал}
tmp.Name:='<'+term+'>';
If (SearchInBlock(y,RTN,tmp)=0) and (term>'') Then
Complete(RTN,tmp);{добавляем правый}
inc(i);{пропуск >}
If s[i]='|' Then
Begin
inc(i);
Goto More;
End;
End
Else{последний в правиле терминал}
Begin
While (i>1) and not((s[i]=' ') or (s[i]='|') or (s[i]='>')) Do dec(i);
inc(i);
Blank;
Terminal(term);
tmp.Name:=term;
If (SearchInBlock(y,RTN,tmp)=0) and (term>'') Then
Complete(RTN,tmp);{добавляем правый}
If s[i]='|' Then
Begin
inc(i);
Goto More;
End;
End;
If i<Len Then{прошли не всю строку}
Goto More;
next:inc(y);
tmp.Name:=#0;{после каждой строки ставим разделитель}
Complete(LTN,tmp);{добавляем левый}
Complete(RTN,tmp);{добавляем правый}
Until y>CLine;
{после цикла получили "предварительные" левые и правые, их еще надо дополнить}
For y:=1 To 10 Do
Begin
Add_(LTn);
Add_(RTn);
End;
{получили левые и правые, разделенные #0}
End;
Procedure Matrix;
Procedure Precede;
Label More,Next;
Var mi,mj:Byte;
tmp:List;
p:NotTerm;
term,term2:String;
Ex:Boolean;
Begin
y:=1;
i:=1;
Repeat
PosStr(y,s);
Blank;
i:=Pos('=',S)+1;{i ставим после :=}
More:Blank;
If s[i]='<' Then
Begin
inc(i);
Blank;
Terminal(term);
tmp.Name:='<'+term+'>';
term2:=tmp.Name;
Blank;
inc(i);
mi:=Search(Trm_notTrm,tmp);
If Terminal(term) Then{нетерминал за ним терминал}
Begin
tmp.Name:=term;
mj:=Search(Trm_notTrm,tmp);
Ex:=matrixprecede[mi,mj]=0;
If not Ex Then
matrixprecede[mi,mj]:=4
Else
matrixprecede[mi,mj]:=3;
p:=RTN;
Seek(term2,RTN,p);
While (p<>Nil) and (p^.Name<>#0) Do
Begin
tmp.Name:=p^.Name;
mi:=Search(Trm_notTrm,tmp);
Ex:=matrixprecede[mi,mj]=0;
If not Ex Then
matrixprecede[mi,mj]:=4
Else
matrixprecede[mi,mj]:=2;
p:=p^.Next;
End;
End
Else
If i>Len Then Goto Next
Else
If s[i]='|' Then
Begin
inc(i);
Goto More;
End;
Blank;
If s[i]='|' Then
Begin
inc(i);
Goto More;
End;
If i<=Len Then{не дошли до конца правила}
Begin
i:=i-Length(term);
While s[i]=' ' Do dec(i);
Goto More;
End;
End
Else
Begin
Terminal(term);
tmp.Name:=term;
mi:=Search(Trm_notTrm,tmp);
Blank;
If i>Len Then{последний в правиле терминал}
Goto Next;
If s[i]='<' Then{за терминалом следует нетерминал}
Begin
inc(i);
Terminal(term);
tmp.Name:='<'+term+'>';
mj:=Search(Trm_notTrm,tmp);
{записываем в матрицу =}
Ex:=matrixprecede[mi,mj]=0;
If not Ex Then
matrixprecede[mi,mj]:=4
Else
matrixprecede[mi,mj]:=3;
p:=LTN;
Seek(tmp.Name,LTN,p);
While (p<>Nil) and (p^.Name<>#0) Do
Begin
tmp.Name:=p^.Name;
mj:=Search(Trm_notTrm,tmp);
Ex:=matrixprecede[mi,mj]=0;
If not Ex Then
matrixprecede[mi,mj]:=4
Else
matrixprecede[mi,mj]:=1;
p:=p^.Next;
End;
Blank;
inc(i);
Blank;
If s[i]='|' Then
Begin
inc(i);
Goto More;
End;
If i<=Len Then{не дошли до конца правила}
Begin
i:=i-Length(term)-2;
Goto More;
End;
End
Else
If i<Len Then
Begin
If s[i]='|' Then
Begin
inc(i);
Goto More;
End;
{за терминалом терминал}
tmp.Name:=term;
mi:=Search(Trm_notTrm,tmp);
Terminal(term);
tmp.Name:=term;
mj:=Search(Trm_notTrm,tmp);
Ex:=matrixprecede[mi,mj]=0;
If not Ex Then
matrixprecede[mi,mj]:=4
Else
matrixprecede[mi,mj]:=3;
i:=i-Length(term);
End;
End;
If i<Len Then{прошли не всю строку}
Goto More;
next:inc(y);
Until y>CLine;
End;
Procedure WrtSymbol(i,j,c:Byte);
Begin
Case c of
1:Begin
OutTextXY(18+i*25,27+j*24-40,'<');
PutPixel(18+i*25+5,27+j*24+3-40,3);
End;
2:Begin
OutTextXY(18+i*25,27+j*24-40,'>');
PutPixel(18+i*25-1,27+j*24+3-40,3);
End;
3:Begin
OutTextXY(18+i*25,25+j*24+3-40,'=');
PutPixel(18+i*25+2,25+j*24+3-40,3);
End;
4:OutTextXY(18+i*25,25+j*24+3-40,'X');
End;
End;
Var sdig:String[2];
j:Byte;
x,y:Byte;
tmp:NotTerm;
tmp2:NotTerm;
Error:Boolean;
Pic:Pointer;
size:Word;
Begin
Message(30,15,15,7,'',False);
Zoom;
Message(30,15,15,7,'Матрица предшествования',False);
Tab(CTrmNotTrm+1,10,20);
WriteGr('ГРАММАТИКА',440,360,200);
For j:=1 To CLine Do
Begin
PosStr(j,s);
LineStr(s,400,375+j*13);
End;
TextColor(14);
TextBackGround(0);
Window(1,1,80,28);
x:=2;
y:=24;
GotoXY(50,2);
WriteLN('Левые Правые');
SetColor(14);
tmp:=Trm_NotTrm;
tmp2:=notTerminalL;
For i:=1 To CTrmNotTrm Do
Begin
Str(i,sdig);
OutTextXY(18+i*25,25,sdig);
OutTextXY(18,35+i*24,sdig);
inc(y);
If y=29 Then
Begin
inc(x,13);
y:=25;
End;
GotoXY(x,y);
TextColor(14);
Write(sdig,'. ');
TextColor(3);
Write(tmp^.Name);
GotoXY(43,2+i);
If tmp2<>Nil Then
Write(tmp2^.Name);
tmp2:=tmp2^.Next;
tmp:=tmp^.Next;
End;
tmp2:=LTN;
i:=3;
GotoXY(50,WhereY);
While tmp2<>Nil Do
Begin
If tmp2^.Name=#0 Then
Begin
GotoXY(50,WhereY);
inc(i);
End;
GotoXY(WhereX,i);
If tmp2^.Name<>#0 Then Write(tmp2^.Name);
tmp2:=tmp2^.Next;
End;
tmp2:=RTN;
i:=3;
GotoXY(70,WhereY);
While tmp2<>Nil Do
Begin
If tmp2^.Name=#0 Then
Begin
GotoXY(70,WhereY);
inc(i);
End;
GotoXY(WhereX,i);
If tmp2^.Name<>#0 Then Write(tmp2^.Name);
tmp2:=tmp2^.Next;
End;
Precede;
SetColor(3);
Error:=False;
For j:=1 To CTrmNotTrm Do{!!!}
For i:=1 To CTrmNotTrm Do{!!!}
Begin
If MatrixPrecede[j,i]=4 Then Error:=True;
WrtSymbol(i,j+2,MatrixPrecede[j,i]);
End;
If Error Then
Begin
TextColor(15);
TextBackGround(1);
Message(30,15,15,7,'Нажмите любую клавишу',True);
VerticalRetrace;
SaveWindow(GraphCooX(20),GraphCooY(12),GraphCooX(62)+1,GraphCooY(19),Pic,size);
TextBackGround(4);
TextColor(14);
OpenWindow(20,12,60,17,3,' Внимание ',True);
WriteLn('Матрица предшествования содержит ошибки');
Write(' Построение функции предшествования ');
Write(' невозможно');
Attention(363,243);
ReadKey;
LoadWindow(GraphCooX(20),GraphCooY(12),size,pic);
End;
End;
{основная программа}
Begin
Init;
InitText;
If InputText Then
Begin
Check;
SearchLR;
Matrix;
ClearBuf;
ReadKey;
End;
GraphWriteOff;
CloseGraph;
End.
1. Грис Д. Конструирование компиляторов для цифровых вычислительных машин. – М.: Мир, 1975.
2. Шамашов М.А. Основные структуры данных и алгоритмы компиляции. – Самара: Университет Наяновой, 1999.
3. Шамашов М.А. Теория формальных языков. Грамматики и автоматы. – Самара: Университет Наяновой, 1996.
4. Интернет сайт. - WWW.CodeNet.ru
Похожие работы
... и определяю- щем вхождении идентификатора. КОНТЕКСТНЫЕ УСЛОВИЯ ЧЕТВЕРТОГО ТИПА Некоторые логические ограничения, которые относятся к реа- лизации той или иной версии транслятора. Массив может быть с неограниченным размером. ЛЕКЦИЯ 17 ПРОГРАММНЫЕ ГРАММАТИКИ Правила вывода этих грамматик имеют тот же вид, что и у классических, однако в ...
... habe die Sommerferien sehr gern. После проведения предэкспериментального среза началось пробное обучение (второй этап), в ходе которого основное внимание было направлено на формирование языковой компетенции учащихся (её грамматического аспекта) с учётом дифференцированного подхода к обучению активной и пассивной грамматике. В рамках учебной программы учащиеся знакомились с таким грамматическим ...
... , в данном каталоге в каждый момент времени может быть активным только один процесс yacc Постановка задачи Реализовать: – транслятор с языка математических выражений на язык деревьев вывода – интерпретатор языка деревьев вывода К разрабатываемым программам предъявляются следующие требования: – реализация осуществляется на языке C++. – функциональность транслятора и интерпретатора должна ...
... 78 IsNumeric 19 2 ( 22 77 A 21 1 ) 23 78 <> 9 67 0 20 3 and 18 1 A 21 1 > 9 66 0 20 3 ) 23 78 Then 11 11 A 21 1 = 1 65 B 21 2 EndIf 11 11 Text 14 14 . 6 74 Text 16 16 = 1 65 A 21 1 End 10 10 Sub 10 10 Отладка формальной грамматики Отладка грамматики – это процесс преобразования грамматики к виду, удовлетворяющему ...


0 комментариев