Навигация
Для отыскания решения требуется экспоненциальное время
1. Для отыскания решения требуется экспоненциальное время.
2. Искомое решение настолько велико, что не может быть представлено в виде выражение, длина которого ограничена некоторым полиномом. Эти задачи в курсе рассматриваться не будут.
Первые результаты о трудно решаемых задачах были получены Тьюрингом. Он доказал, что некоторые задачи “неразрешимы” в том смысле, что вообще не существует алгоритма их решения. Некоторые задачи по теории автоматов, теории формальных языков и математической логики являются трудно решаемыми.
NP-полная задача - это задача, к которой сводится за полиномиальной время любая задача из класса NP-задач. Фундаментальные исследования и теорию NP-задач разработал С.Кук в 1971 году. Им определено понятие сводимости за полиномиальное время. Если одна задача сводится за полиномиальное время к другой, то любой полиномиальный алгоритм - решение другой задачи может быть превращен в полиномиальный алгоритм первой задачи.
Выделен класс задач распознавания свойств, которые могут быть решены за полиномиальное время на недетерминированном вычислительном устройстве. Доказано, что любая задача из класса NP-задач может быть сведена к задаче выполнимой за полиномиальное время.
Существуют 6 основных классов NP-полных задач:
1. Задачи выполнимости.
2. Трехмерное сочетание.
3. Вершинное покрытие.
4. Поиск клики.
5. Гамильтонов цикл.
6. Разбиение.
- внутренние параметры - характеризуют свойства элементов ;
- выходные параметры - характеризуют свойства систем;
- ограничения выходных параметров.
ПРИМЕР 3.
Применительно к операционному усилителю:
а) переменные
- фазовые переменные - напряжение и токи всех ветвей (рассматриваются как функции времени или частоты);
б) параметры
- внешние параметры - напряжения источников питания, параметры входных сигналов и нагрузки, температура окружающей среды;
- внутренние параметры - номиналы резисторов, барьерные емкости и тепловые токи переходов в транзисторах, емкости конденсаторов;
- выходные параметры - коэффициент усиления на средних частотах, полоса пропускания, потребляемая мощность, динамический диапазон;
- ограничения - верхние границы допустимых значений коэффициентов усиления, полосы пропускания, динамического диапазона.
Применительно к вычислительной системе:
а) переменные
- фазовые переменные - состояния отдельных устройств;
б) параметры
- внешние параметры - параметры входных источников заявок;
- внутренние параметры - емкости запоминающих устройств, быстродействие процессоров, число каналов;
- выходные параметры - производительность системы, коэффициент загрузки оборудования, вероятность решения поступающих задач, средние длины очередей заявок на обслуживание;
- ограничения - нижние границы допустимых диапазонов значений производительности, коэффициентов загрузки оборудования, вероятности обслуживания заявок.
При блочно-иерархическом подходе внутренние параметры k -го уровня являются выходными параметры (k+1) -го уровня. При многоаспектном рассмотрении систем, включающих физически разнородные подсистемы, роль внешних переменных для данной подсистемы играют фазовые переменные других подсистем. Они влияют на рассматриваемую подсистему.
Внутренние параметры являются случайными величинами из-за разброса параметров комплектующих изделий, материалов и нестабильности условий изговления. Выходные параметры также имеют случайный характер следствие случайных значений внутренних параметров.
4. Классификация проектных процедур.
Классификация проектных процедур приведена в табл.1.
ТАБЛИЦА 1. ПРОЕКТНЫЕ ПРОЦЕДУРЫ
| АНАЛИЗ | СИНТЕЗ |
| Одновариантный Многовариантный | Параметрический Структурный |
| Статики Чувствительности Динамики Статистический В частной области Расчет зависимостей выходных параметров Стационарных режимов от внутренних и внешних параметров Устойчивости | Расчет внутренних параметров Оптимизация параметров Оптимизация допусков Оптимизация технических требований |
В процедурах анализа оцениваются варианты построения объектов, а в процедурах синтеза - разрабатываются.
Одновариантный анализ заключается в определении вектора выходных параметров Y при заданных:
- структуре системы,
- значениях векторов параметров элементов X,
- значениях внешних параметров Q.
Структура системы задана, если заданы перечень типов элементов и способ их связи друг с другом в составе системы. По известной структуре и значениям X и Q могут быть созданы физическая или математическая модели и по результатам исследования модели оценены значения gпараметров вектора Y.
Приемлемость полученных значений выходных параметров из вектора Y определяется путем сопоставления их со значениями параметров из вектора T, указанных в техническом задании (ТЗ).
Требуемое по ТЗ соотношение между значениями параметров yi и ti , i=1,n называют условием работоспособности по параметру yi.
Условия работоспособности могут быть представлены в следующем виде:
yi = t i, (2)
tнi = > = 0 ,
где скобки обозначают усреднение по времени.
Уравнения (9) и (10) описывают существенно различные физические процессы, которые в рассматриваемом контексте можно назвать "обучением" и "распознаванием образов". Рассмотрим первое из них. Обучение состоит в том, что в (9) включается сильное внешнее поле, действующее в течение времени t . В результате того вектор m(t) принимает стационарное значение fi , соответствующее "образу" с компонентами m . После "обучения" элементы матрицы , со временем в соответствии с уравнением (10), получат приращение ( при этом предполагается, что t значительно больше времени релаксации на внешнем поле вектора m к своему стационарному значению fi ). Процедуру обучения можно повторить многократно, используя образы fi , s=1,...,n. Считая, что до начала обучения = 0, после окончания этого процесса получим
,
где коэффициенты nu зависят от длительности обучения. Таким образом, уравнения (9) и (10) описывают процесс запоминания поступающей в систему информации в виде матриц связей хеббовского вида.
Ранее предполагалось, что до начала обучения нейронная сеть не содержит никакой информации, = 0. Можно рассмотреть противоположный случай, когда до начала обучения нейронная сеть имеет большое число устойчивых состояний. Предполагается, что доминируют глубокие энергетические минимумы, которые могут образовывать структуру дерева. Процедура обучения должна приводить к селекции образов . В процессе обучения заучиваемый образ задается в качестве начального состояния сети и эволюционирует к некоторому аттрактору, энергия которого уменьшается за счет синоптических изменений ( в частности, если время релаксации меньше времени обучения), а область притяжения смещается и увеличивается за счет
присоединения соседних областей. Таким образом, процесс селекции отличается от режима обучения, рассмотренного ранее тем что используется внешнее поле.
ОСНОВНЫЕ ФУНКЦИИ НЕЙРОННЫХ СЕТЕЙ
АССОЦИАТИВНАЯ ПАМЯТЬ И КАТЕГОРИЗАЦИЯ
Под ассоциативной памятью ( или памятью, адресуемой по содержанию) понимается способность системы нейронов, например, мозга млекопитающих восстанавливать точную информацию по некоторой
ее части. К этому определению близок процесс категоризации - отнесение предъявленного объекта к одному из классов. Многие из предложенных в настоящее время сетей способны фактически осуществлять эти функции. При этом критерии, по которым осуществляется отнесение объектов к тому или иному классу ( распознавание) , различны в разных моделях.
Рассмотрим в качестве примера модель Хопфилда.
Пусть сначала n=1 b и в матрице Т записан всего один образ fi . Скалярноe произведение произвольного вектора m и fi задается выражением (fi , m ) = N - 2 m, где m - хеммингово расстояние между векторами m и fi, равное числу элементов, отличающих эти векторы. Подставляя это выражение в ( 7 ), получим следующее выражение для энергии:
.
Из данного выражения видно, что Е принимает минимальное значение при m=0. При этом вектор М совпадает с записанным образом либо, когда m=N ( в этом случае m совпадает с "негативом" ). Поэтому эволюция любого начального состояния системы заканчивается в состояниях m = fi .
В случае n = 2 выражение для энергии имеет вид
.
Здесь N - число позиций, в которых компоненты записанных в Т векторов совпадают: fi= fi , N- число несовпадающих компонент этих векторов, для которых fi=- fi , m и m - число компонент вектора m в первой и во второй группе нейронов соответственно, отличающих m от fi . Из последнего выражения видно, что система нейронов имеет четыре устойчивых состояния, отвечающих m = 0,N , m =0,N . При этом они совпадают с одним из векторов fi,= fi.
Функцию категоризации могут осуществлять нейронные сети других типов, при этом каждая из сетей делает это по разному. Так, если сеть Хопфилда относит к одному устойчивому вектору все стимулы, попавшие в область его зоны притяжения, то сеть Хемминга относит каждый входной вектор к ближайшему вектору, записанному в память.
ВЫРАБОТКА ПРОТОТИПА И ОБОБЩЕНИЕ
Различные типы нейронных сетей допускают возможность их обучения для выполнения алгоритмов обработки входной информации. При этом в обучающей выборке может не содержаться полного описания
предлагаемых алгоритмов.
Рассмотрим два примера:
- выработка прототипа в модели Хопфилда ( образование устойчивого образа в памяти, не содержавшегося среди обучаемых векторов),
- обобщение по индукции.
При увеличении числа образов в памяти минимальные значения энергии, вычисленные с помощью выражения (7) и соответствующие различным записанным векторам, могут начать сливаться.
Рассмотрим группу образов fi ( s=1,...,n) , получающихся при небольших случайных искажениях del некоторого вектора fi .
При изменении вектора fi на величину del происходит изменение энергии, соответствующей этому вектору, на величину del E.
При и случайном искажении исходного вектора fi при построении группы образов может выполняться неравенство del E 0 и следовательно, исходный вектор отвечает минимуму энергии системы. В психологии образ, аналогичный fi ( т.е. являющийся в определенном смысле усреднением некоторого числа образов и остающийся в памяти человека наряду с действительно предъявлявшимися образами) , получил название прототипа.
Сущность обобщения по индукции можно понять на следующем примере. Предположим, что множество входов сети разделено на две части, кодирующие соответственно два "образа". Например, это могут быть два числа либо два изображения предметов. Выходной слой персептрона пусть содержит один бинарный нейрон. При обучении будем стремиться к тому , чтобы на выходе сети была 1, если образы на входе совпадают и 0 , в противном случае. Установлено, что трехслойная сеть может быть обучена по указанному правилу, и способна определять совпадение образов на входе ( или симметрию входного вектора, что в данном случае одно и то же). Таким образом, сеть по индукции обучается устанавливать совпадение двух
векторов, хотя при обучении явное определение понятия совпадение не приводилось. По этому же принципу можно обучить нейронную сеть складывать числа.
ЗАКЛЮЧЕНИЕ
Практические процедуры обучения нейронных сетей часто сталкиваются с невозможностью добиться от сети желаемого поведения. Ранее упоминались некоторые проблемы такого рода:
- отсутствие сходимости процесса обучения персептронов,
- ложная память в модели Хопфилда.
Причины этого могут разделены на две группы.
1. Значительное время обучения нейронных сетей в сложных случаях.
2. Принципиальная невозможность получения необходимой структуры фазового пространства в заданной модели нейронной сети.
Область приложения нейронных сетей значительна и расширяется.
Этот процесс идет по ряду направлений. К их числу можно отнести следующие:
- поиск новых нелинейных элементов , которые могли бы реализовывать сложное коллективное поведение в ансамбле,
- разработка новых архитектур нейронных сетей, перспективных с точки зрения их реализации на электронной, оптической и оптоэлектронной элементной базе,
- поиск областей приложения нейронных сетей в системах управления, робототехнике, системах обработки изображений, распознавания речи.
ЛЕКЦИЯ №3
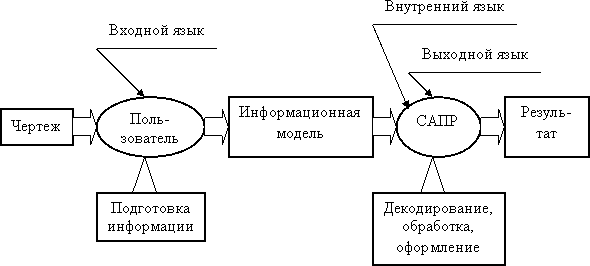
СИСТЕМА АВТОМАТИЧЕСКОГО ВВОДА ИНФОРМАЦИИ В ЭВМ
Похожие работы
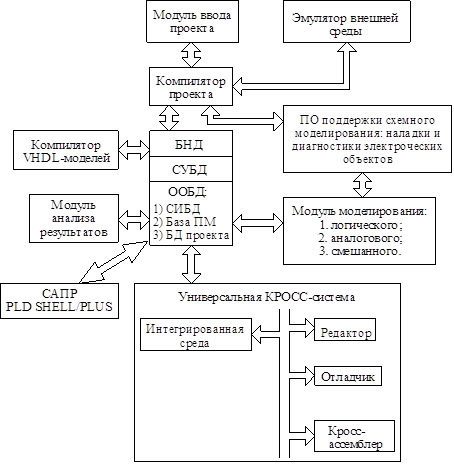
... литературе как "рабочая станция" (PC). Рис. 3. Структура рабочей станции проектирования электронных систем. Рис. 4. Структура ПО САПР. 4. Иерархические уровни представления электронных устройств Основным методом проектирования с применением САПР является блочно-иерархический метод или метод декомпозиции сложного объекта на подсистемы (блоки, узлы, компоненты). В этом случае ...
... него среде, знакомой ему по версии "AutoCAD 14. Однако более 400 усовершенствований делают работу конструктора существенно удобней и проще. 2. Технология автоматизированного проектирования в системе AutoCAD 2.1 Основы AutoCAD Чертить в системе AutoCAD — значит, формировать на экране дисплея изображение из отдельных графических элементов (примитивов), которые вводятся при помощи ...
... актуальностью информации, идентифицировать ошибки и избежать перепроектирования (по оценкам компании Aberdeen, не менее 70 % затрат на производство и сопровождение продукции приходится на этап проектирования). PLM-система способна предоставить пользователю информацию в форме, соответствующей выполняемым функциям в жизненном цикле создаваемого продукта: трехмерные модели, схематические диаграммы, ...
... являются Лоцман:PLM компании Аскон, PDM STEP Suite, разработанная под НПО "Прикладная логистика", Party Plus компании Лоция-Софт и т.д. Итак, термин САПР (система автоматизации проектирования) подразумевает комплексный подход к разработке изделия и включает совокупность систем CAD/CAM/CAE. Развитие систем геометрического моделирования, анализа и расчета характеристик изделия сопровождается ...


0 комментариев