Отличие
ЭС от других
программных
продуктов
Области
применения
экспертных
систем
Проблемы,
возникающие
при созданииЭС.
Перспективы
разработки
Критерий
пользователя
ЭС
Подсистема
вывода
Компонент
вывода
Диалог
с ЭС. Объяснение
Разработка
стратегии
Представление
задач в пространстве
состояний
Запись
в виде графа
Метод
равных цен
Изменение
при переборе
на произвольных
графах
Использование
других эвристик
Навигация
Метод равных цен
Экспертные системы. Классификация экспертных систем. Разработка простейшей экспертной системы
102315
знаков
3
таблицы
0
изображений
4.2.2 Метод равных цен.
Могут встретится задачи, в которых решению предъявляются какие-то иные требования, отличные от требования получения наикратчайшей последовательности операторов. Присваивание дугам деревьев определенных цен (с последующим нахождением решающего пути, имеющего минимальную стоимость) соответствует многим из таких обещанных критериев. Более общий вариант метода полного перебора, называемый методом равных цен, позволяет во всех случаях найти некоторый путь от начальной вершины к целевой, стоимость которого минимальна. В то время как в выше описанном алгоритме распространяются линии равной длины пути от начальной вершины, в более общем алгоритме, который будет описан ниже, распространяются линии равной стоимости пути. Предполагается, что нам задана функция стоимости c(ni,nj), дающая стоимость перехода от вершины ni к некоторой следующей за ней вершине nj.
В методе равных цен для каждой вершины n в дереве перебора нам нужно помнить стоимость пути, построенного от начальной вершины s к вершине n. Пусть g(n)- стоимость от вершины s к вершине n в дереве перебора. В случае деревьев перебора мы можем быть уверены, что g(n) является к тому же стоимостью того пути, который имеет минимальную стоимость (т.к. этот путь единственный).
В методе равных цен вершины раскрываются в порядке возрастания стоимости g(n). Этот метод характеризуется такой последовательностью шагов:
1) Поместить начальную вершину s в список, называемый ОТКРЫТ. Положить g(s)=0.
2) Если список ОТКРЫТ пуст, то на выход подается сигнал о неудаче поиска, в противном случае переходить к следующему шагу.
3) Взять из списка ОТКРЫТ ту вершину, для которой величина g имеет наименьшее значение, и поместить ее в список ЗАКРЫТ. Дать этой вершине название n. (В случае совпадения значений выбирать вершину с минимальными g произвольно, но всегда отдавая предпочтение целевой вершине.)
4) Если n есть целевая вершина, то на выход выдать решающий путь, получаемый путем просмотра назад в соответствии с указателями; в противном случае переходить к следующему шагу.
5) Раскрыть вершину n, построив все непосредственно следующие за ней вершины. (Если таковых нет переходить к шагу (2).) Для каждой из такой непосредственно следующей (дочерней) вершины ni вычислить стоимость g(n), положив g(ni)=g(n)+c(n,ni). Поместить эти вершины вместе с соответствующими им только что найденными значениями g в список ОТКРЫТ и построить указатели, идущие назад к n.
6) Перейти к шагу (2).
Блок- схема этого алгоритма показана на рис.7. Проверка того, является ли некоторая вершина целевой, включена в эту схему так, что гарантируется обнаружение путей минимальной стоимости.
Алгоритм, работающий по методу равных цен, может быть также использован для поиска путей минимальной длины, если просто положить стоимость каждого ребра равной единице. Если имеется несколько начальных вершин, о алгоритм просто модифицируется: на шаге (1) все начальные вершины помещаются в список ОТКРЫТ. Если состояния, отвечающие поставленной цели, могут быть описаны явно, то процесс перебора можно пустить в обратном направлении, приняв целевые вершины в качестве начальных и используя обращение оператора Г.
Пуск
Поместить s в список ОТКРЫТ.
Положить g(s)=0.
нет Пуст ли да
список неудача
ОТКРЫТ?
Взять из списка ОТКРЫТ вершину
с наименьшим значением g
и поместить ее в список ЗАКРЫТ.
Обозначить ее через n.
нет Является ли n да успех
вершиной цели?
Раскрыть n. Вычислить значение g
для дочерних вершин.
Поместить эти вершины в список ОТКРЫТ.
Провести от них указатели к n.
рис.7 Блок- схема программы алгоритма равных цен для деревьев.
4.3 Метод перебора в глубину.
В методах перебора в глубину прежде всего раскрываются те вершины, которые были построены последними. Определим глубину вершины дереве следующим образом:
Глубина корня дерева равна нулю.
Глубина любой последующей вершины равна единице плюс глубина вершины, которая непосредственно ей предшествует.
Таким образом, вершиной, имеющей наибольшую глубину в дереве перебора, в данный момент служит та, которая должна в этот момент быть раскрыта.
Такой подход может привести к процессу, разворачивающемуся вдоль некоторого бесполезного пути, поэтому нужно ввести некоторую процедуру возвращения. После того как в ходе процесса строится вершина с глубиной, превышающей некоторую граничную глубину, мы раскрываем вершины наибольшей глубины, не превышающей этой границы и т.д.
Метод перебора в глубину определяется следующей последовательностью шагов:
1) Поместить начальную вершину в список, называемый ОТКРЫТ.
2) Если список ОТКРЫТ пуст, то на выход подается сигнал о неудаче поиска, в противном случае перейти к шагу (3).
3) Взять первую вершину из списка ОТКРЫТ и перенести в список ЗАКРЫТ. Дать этой вершине название n.
4) Если глубина вершины n равна граничной глубине, то переходить к (2), в противном случае к (5).
5) Раскрыть вершину n, построив все непосредственно следующие за ней вершины. Поместить их (в произвольном порядке) в начало списка ОТКРЫТ и построить указатели, идущие от них к n.
6) Если одна из этих вершин целевая, то на выход выдать решение , просматривая для этого соответствующие указатели, в противном случае переходить к шагу (2).
На рис.8 приведена блок- схема для метода перебора в глубину.
Пуск
Поместить s в список ОТКРЫТ.
нет Пуст ли да
список неудача
ОТКРЫТ?
Взять первую вершину из списка
ОТКРЫТ
и поместить ее в список ЗАКРЫТ.
Обозначить ее через n.
да Равна ли глубина нет
n граничной глубине
Раскрыть n. Вычислить значение g
для дочерних вершин.
Поместить эти вершины в список ОТКРЫТ.
Провести от них указатели к n
Являются ли
нет какие- либо да
из дочерних вершин успех
целевыми?
рис.8 Блок-схема программы алгоритма поиска в глубину для деревьев.
В алгоритме поиска в глубину сначала идет перебор вдоль одного пути, пока не будет достигнута максимальная глубина, затем рассматриваются альтернативные пути той же или меньшей глубины, которые отличаются от него лишь последним шагом, после чего рассматриваются пути, отмечающимися последними двумя шагами, и т.д.
Похожие работы
... охватывало бы вопросы воспитания, взаимодействия учителей с родителями учеников и самими учениками, вопросы самоподготовки желающих учиться учеников, помощи отстающим и т.п. 5. РАЗРАБОТКА ШКОЛЬНОЙ ИНФОРМАЦИОННОЙ СИСТЕМЫ (ШИС) НА ОСНОВЕ IT-ТЕХНОЛОГИЙ ДЛЯ МОУ СОШ № 97 Поставленные в предыдущем разделе задачи могут быть решены путем организации широчайшего (относительно родителей, учеников и ...
... основании вышеуказанных протоколов проводится окончательная оценка соответствия средства размещения определенной категории. Средства размещения определенной категории должны соответствовать: гостиницы, мотели и пр. с количеством номеров более 50: - требованиям, определенным в таблицах приложения к системе классификации; - критериям балльной оценки (табл. 2) с учетом следующего суммарного ...
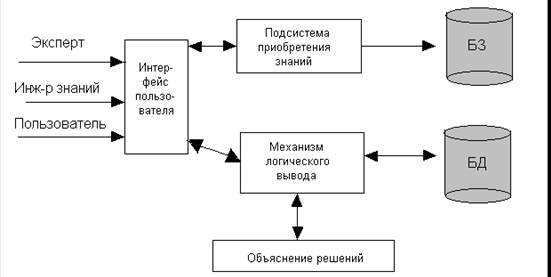
... профессиональных знаний из экспертов и проектирование базы знаний экспертной системы и ее архитектуры. Программист необходим при разработке специализированного для данной экспертной системы программного обеспечения, когда подходящего стандартного (например, оболочки для создания экспертных систем) не существует или его возможностей не достаточно и требуются дополнительные модули. В процессе ...
... системы управления (АСУ); автоматизированные системы информационного обеспечения (АСИО). Рассмотрим каждый из перечисленных в классификации типов АИС подробнее. Под автоматизированной информационно-справочной системой (АИСС) в области права будем понимать автоматизированную информационную систему, предназначенную для сбора, систематизации, хранения и поиска правовой информации по запросам ...
0 комментариев