Навигация
Определение корреляционной функции сигнала
1.4. Определение корреляционной функции сигнала.
Для случайного сигнала с заданным энергетическим спектром W(w) определить:
а) Корреляционную функцию K(t);
б) эффективную ширину спектра;
в) интервал корреляции.
Изобразить графики W(w) и K(t), показать на них эффективную ширину спектра и интервал корреляции.
1.5. Нелинейное преобразование сигналов.
Стационарный гауссовский случайный процесс u(t) с параметрами m(t) и s(t) воздействует на безынерционную нелинейную цепь с характеристикой, заданной в варианте.
Определить плотность распределения вероятностей w(y) процесса на выходе цепи y(t), его математическое ожидание, дисперсию и среднеквадратическое отклонение.
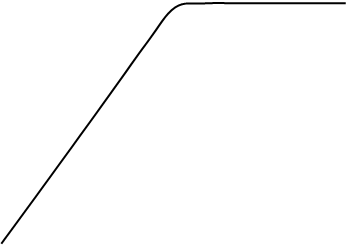
Построить графики входного и выходного процессов относительно заданной передаточной характеристики безынерционной нелинейной цепи и соответствующих им плотностей распределения вероятностей мгновенных значений w(uвх) и w(y). Показать на них mx, sx, my, sy.
Графики должны быть построены с учетом заданных параметров входного процесса и цепи.
4.
Помехоустойчивое кодирование и декодирование поясняется для случая использования кода с проверкой на четность.
1.
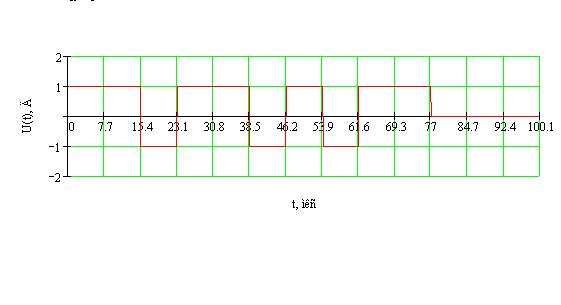
2. В основе выполнения пункта 1.3. лежит определение плотности распределения вероятностей мгновенных значений по временной реализации U(t) эргодического сигнала длительностью T. При этом плотность распределения вероятностей определяется соотношением вида
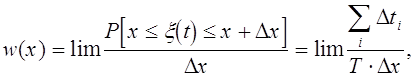
Dx®0 T®¥
Dx®0
где  представляет собой относительное время пребывания зна-
представляет собой относительное время пребывания зна-
T®¥ чений реализации в интервале от x до (x+Dx).
В курсовой работе используется графический (“ручной”) способ определения ![]() времени пребывания значений случайного напряжения Ui(t) в интервале от U до (U+DU) для различных U. При этом получаем гистограмму распределения вероятностей. По определению
времени пребывания значений случайного напряжения Ui(t) в интервале от U до (U+DU) для различных U. При этом получаем гистограмму распределения вероятностей. По определению

следовательно, 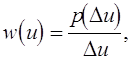 т.е. в общем случае w(u) получается путем аппроксимации (сглаживания) гистограммы распределения вероятностей непрерывной кривой или ожидаемым законом распределения.
т.е. в общем случае w(u) получается путем аппроксимации (сглаживания) гистограммы распределения вероятностей непрерывной кривой или ожидаемым законом распределения.
Описанные выше соотношения должны удовлетворять условию нормировки
P[- ¥ < xi(t) < ¥] = 1 для 0 £ t £ T
и, соответственно,
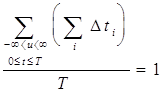
Для интервала времени, на котором напряжение является постоянным на некотором уровне U0, плотность распределения вероятностей представляет собой дельта-функцию d(u - U0), удовлетворяющую условию нормировки
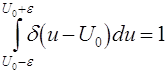
Выражения для плотности и функции распределения вероятностей должны быть заданы (описаны) для диапазона изменения значений и в пределах от - ¥ до ¥. Если w(u) содержит дельта-функцию, то она обозначается как p(U0) × d(u-U0 ) , где p(U0) - вероятность значения U0. В функции распределения F(u) при значении u = U0 будет скачок на величину p(U0). Выражение и график F(u) должны удовлетворять условию "неубываемости" ее в пределах - ¥ < u< ¥.
Вероятность попадания значений сигнала в заданный интервал
U1 £ u £ U2 определяется через плотность распределения вероятностей известным соотношением

3. При выполнении пункта 1.4 рекомендуется для упрощения расчетов учитывать особенность определения функции корреляции узкополосного случайного процесса. Получаемые выражения целесообразно приводить к виду, близкому к табличному или к виду характерных функций, например, sin(x)/x, sin2(x)/x2, что упрощает расчеты. В приложении 1 приведен справочный материал для интегралов, встречающихся в работе подинтегральных выражений.
Эффективная ширина спектра Dfэфф и интервал корреляции t0 следует определять по функции энергетического спектра и функции корреляции соответственно. Выражение для связи между Dfэфф и t0 рекомендуется использовать только для проверки правильности расчетов.
Для удобства расчетов и построения графиков энергетического спектра W(w) и функции корреляции B(t) значения w и t можно задавать в виде
w = k ×a, t = k ×1/a, где k - числа 0, 0,5, 1,0, 1,5, 2, и т.д., что позволяет упростить расчет. Однако, при этом оси w и t графиков W(w) и B(t) должны быть промасштабированы и в абсолютных значениях w и t.
Примечание: целесообразно график энергетического спектра строить как функцию линейной частоты W(f) и определять, соответствен- но, Dfэфф.
4. Целью выполнения пункта 1.5 является закрепление навыков нахождения плотности распределения и числовых характеристик процесса на выходе нелинейных безынерционных устройств с заданной передаточной характеристикой. В варианте курсовой работы заданы характеристики наиболее распространенных нелинейных радиотехнических устройств.
Плотность распределения мгновенных значений процесса на выходе w(y) представляется через известное распределение входного процесса w(x)
на основе соотношения для функционально связанных величин y = f(x).
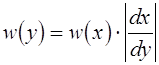 ,
,
или с учетом обратной функции x = j(y) соотношением вида
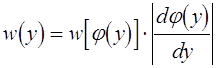 .
.
В случае, когда обратная функция x = j(y) неоднозназначна, то
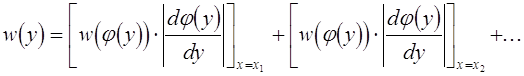 ,
,
где x1, x2, ... - значения входной величины x, соответствующие рассматриваемому значению y.
Если характеристика y = f(x) постоянна на некотором интервале изменения x, то w(y) будет содержать слагаемое с дельта-функцией, учитывающее интегральную вероятность пребывания x ниже (или выше) определенного уровня.
При вычислениях w(y) для гауссовского процесса на входе возникает необходимость вводить табулированную переменную 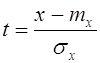 , чтобы воспользоваться таблицами интегральных форм для нормального закона (см. приложение 1). При этом необходимо помнить, что пределы интегрирования должны быть также изменены с учетом вида новой переменной t. В случае необходимости выражения интегралов приводятся к табличному виду. Если интегралы не имеют явного решения, необходимо применять численные методы вычислительной математики.
, чтобы воспользоваться таблицами интегральных форм для нормального закона (см. приложение 1). При этом необходимо помнить, что пределы интегрирования должны быть также изменены с учетом вида новой переменной t. В случае необходимости выражения интегралов приводятся к табличному виду. Если интегралы не имеют явного решения, необходимо применять численные методы вычислительной математики.
Расчеты и построения графиков должны соответствовать условию нормировки (см. п.2).
 и
и  .
.
В приложении 2 приведены значения табулированных функций j(x) и f0(x).
5. В пояснительной записке к курсовой работе должны быть введение и заключение. Во введении формулируются цели курсовой работы по каждому из пунктов с учетом значимости их содержания в инженерной подготовке. В заключении дается краткий анализ результатов с отражением их особенностей.
6. Библиография используемой литературы должна быть составлена в соответствии с существующими требованиями (см. список литературы).
ЛИТЕРАТУРА
1. Гоноровский И.С. Радиотехнические цепи и сигналы: Учебник для вузов. – 4-е изд., перераб. и доп. – М.: Радио и связь, 1986. – 512 с.
2. Гоноровский И.С., Демин М.П. Радиотехнические цепи и сигналы: Учебник для вузов. – 5-е изд., перераб. и доп. – М.: Радио и связь, 1994. – 480с.
3. Баскаков С.И. Радиотехнические цепи и сигналы: Учебник для вузов по спец. “ Радиотехника”. – 2-е изд., перераб. и доп. – М.: Высш. шк., 1988. – 448 с.
Похожие работы
... K(p) - операторный коэффициент передачи цепи 2 ЗАДАНИЕ НА КУРСОВУЮ РАБОТУ Студенту группы 9341 Прокопьева К.В. Учебная дисциплина “Радиотехнические цепи и сигналы” 2.1 Тема работы Анализ радиотехнических сигналов и их прохождение через линейные цепи. 2.2 Цель работы Анализ радиотехнических сигналов и линейных цепей методами математического ...
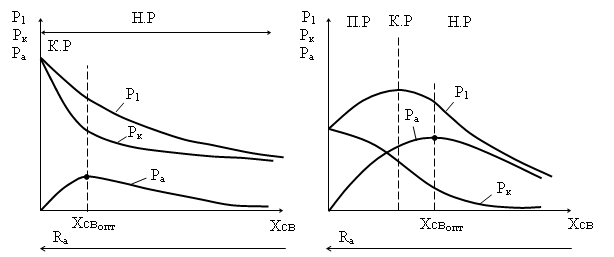
... в антенном контуре Р1=РА+РК – колебательная мощность на выходе генератора hК=РН/Р1 По данным таблиц 1 и 2 были построены нагрузочные характеристики лампового генератора с двухконтурной цепью связи с нагрузкой, полученные экспериментальным путем. Экспериментальные нагрузочные характеристики приведены на графиках 1¸6. График 1. Rахх = 4Rак Rахх = Rак ...
... фильтра является величиной конечной. так как отклик фильтра не может появиться раньше чем придет воздействие то to ³ Tc. 2) длительность Tc < ¥ Þ оптимальная фильтрация применима лишь для импульсных сигналов. При синтезе СФ в качестве входного аналогового сигнала в курсовой работе используется импульсный сигнал, построенный в соответствии с какой либо бинарной кодовой ...
... отношению к малому сигналу НЭ является линейным, но с переменным параметром (в данном случае крутизной ВАХ). Такой режим работы НЭ называется параметрическим. 1. Аппроксимация характеристик нелинейных элементов При анализе нелинейных цепей (НЦ) обычно не рассматривают процессы, происходящие внутри элементов, составляющих эту цепь, а ограничиваются лишь внешними их характеристиками. Обычно это ...


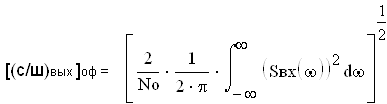

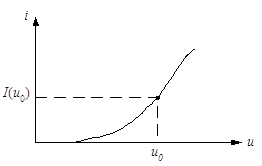
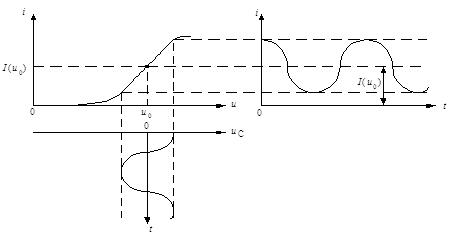

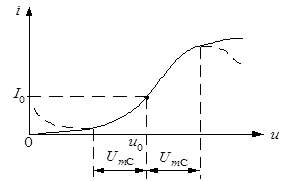
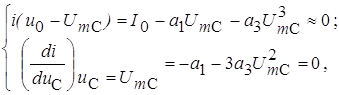
0 комментариев