Навигация
Статистическое (эффективное) кодирование
2.6 Статистическое (эффективное) кодирование.
Статистическое кодирование – прямая противоположность помехоустойчивому кодированию.
При помехоустойчивом кодировании увеличивается избыточность за счет введения дополнительных элементов в кодовой комбинации (например, проверка на четность) благодаря чему повышается избыточность кода.
При статистическом кодировании наоборот, уменьшается избыточность, - наиболее часто встречающиеся сообщения (с большей вероятностью) представляются в виде коротких комбинаций, реже встречающимся сообщениям присваиваются более длинные комбинации, благодаря чему уменьшается избыточность кода.
Производительность источника сообщений определяется количеством передаваемой информации за единицу времени.
Количество информации i(a) - это логарифмическая функция вероятности logP(a), где а - конкретное сообщение из ансамбля А (а Î А)
i(a)= -logP(a)=log(1/P(a)). Основание логарифма берут равным 2. Количество информации, содержащейся в сообщении с вероятностью Р(а)=0.5; i(a)= log 2 (1/0.5) = 1 называется двоичная единица, или бит. Энтропия источника сообщений H(A) - это математическое ожидание (среднее арифметическое) количества информации H(A)=, или усреднение по всему ансамблю сообщений. Рассчитаем энтропию заданного источника Рассчитаем значение энтропии для случая, когда количество сообщений К = 2, а вероятности этих сообщений распределены следующим образом: р(1)=0.1, р(0)=0.9, тогда
Максимальное значение энтропии (Н(А) = 1) для двух сообщений можно получить только в том случае, когда их вероятности равны друг другу, т.е. р(1)= р(0)=0.5. А сравнивая нашу полученную энтропию с максимальной видим, что максимальная больше в два раза. Это достаточно плохо, потому что энтропия связана с производительностью источника Н'(А), которая определяет среднее количество информации, выдаваемое источником в единицу времени:
Н'(А) = Н(А)/Т
где Т – длительность элементарной посылки.
Рассчитаем значение Н'(А) для Т = 5 мкс: Н'(А) = 0.469/5×10-6 = 93800 бит.
Повышение значения производительности источника в нашем случае можно сделать за счет применения статистического кодирования. Пусть ансамбль сообщений А содержит К=8 сообщений, К - объем алфавита. Вероятности этих сообщений будут следующие:
Р(000)=0.9×0.9×0.9= 0,729
Р(001)= Р(010)= Р(100)= 0.9×0.9×0.1 = 0,081
Р(011)= Р(101)= Р(110)= 0.9×0.1×0.1 = 0,009
Р(111)= 0.1×0.1×0.1 = 0,001
Осуществим статистическое кодирование 8 трехбуквенных комбинаций, состоящих из элементов двоичного кода 0 и 1, методом Хаффмена.
Методика Шеннона-Фано не всегда приводит к однозначному построению кода. От указанного недостатка свободна методика построения кода Хаффмана. Она гарантирует однозначное построение кода с наименьшим, для данного распределения вероятностей, средним числом символов на группу.
Суть его сводится к тому, что наиболее вероятным исходным комбинациям присваиваются более короткие преобразованные комбинации, а наименее вероятным - более длинные. За счет этого среднее время, затраченное на посылку одной кодовой комбинации, становится меньше.
Для двоичного кода методика сводится к следующему:
1. Буквы алфавита выписываются в основной столбец в порядке убывания вероятностей.
2. Две последние буквы, с наименьшими вероятностями, объединяют в одну и приписывают ей суммарную вероятность объединяемых букв.
3. Буквы алфавита сортируются заново.
4. Операции 1-3 повторяются.
Процесс повторяется до тех пор, пока не получим единственную букву с вероятностью равной 1.
Таблица 1
| Комбинации | Буквы | Вероятности | Вспомогательные столбцы | ||||||
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
| 000 | Z0 | 0,729 | 0,729 | 0,729 | 0,729 | 0,729 | 0,729 | 0,729 | 1 |
| 001 | Z1 | 0,081 | 0,081 | 0,081 | 0,081 | 0,081 | 0,162 | 0,271 | |
| 010 | Z2 | 0,081 | 0,081 | 0,081 | 0,081 | 0,081 | 0,109 | ||
| 100 | Z3 | 0,081 | 0,081 | 0,081 | 0,081 | 0,109 | |||
| 011 | Z4 | 0,009 | 0,009 | 0,018 | 0,028 | ||||
| 101 | Z5 | 0,009 | 0,009 | 0,010 | |||||
| 110 | Z6 | 0,009 | 0,010 | ||||||
| 111 | Z7 | 0,001 | |||||||
Согласно таблице 6.1. строим граф кодового дерева по следующему правилу:
Из точки с вероятностью «1» направляем две ветви. Ветви с большей вероятностью приписываем 1 и откладываем влево, а ветви с меньшей вероятностью приписываем 0 и откладываем вправо. Такое последовательное ветвление продолжим до тех пор, пока не дойдем до вероятности каждой отдельной буквы. Кодовое дерево изображено на рисунке 6.1. Теперь двигаясь по кодовому дереву с верху вниз можно для каждой буквы записать новую кодовую комбинацию.
1 0 0.271 0 0.109 0 0.028 0 0.010 0 Z7(0.001)
1 1 1 1 1
Z0(0.729) 0.162 Z3 (0.081) 0.018 Z6(0.009)1 0 1 0
Z1(0.081) Z2(0.081) Z4(0.009) Z5(0.009)Рис. Граф кодового дерева.
Получили новые кодовые комбинации:
| Z0 | Z1 | Z2 | Z3 | Z4 | Z5 | Z6 | Z7 |
| 1 | 011 | 010 | 001 | 00011 | 00010 | 00001 | 00000 |
Определим среднюю длину полученных комбинаций по формуле:
lср = k×p(а0)+...+ k×p(аК-1); где К - объем алфавита источника, к - число повторений элемента в кодовом дереве, р(..) - вероятности элементов.
Для полученного кода средняя длина комбинаций =1×p(Z0)+ 3×p(Z1)+ 3×p(Z2)+ 3×p(Z3)+ 5×p(Z4)+5×p(Z5)+5×p(Z6)+5×p(Z7)= 0,729+(3×0,081)+(3×0,081)+(3×0,081)+(5×0,009)+(5×0,009)+(5×0,009)+(5×0,001)= 1,59(бит/элемент)
Эта средняя длина меньше 3Т, но фактически полученные комбинации содержат информацию о трех элементарных сигналах, поэтому средняя длина новых комбинаций в расчете на 1 букву первоначального двоичного кода составляет: 1,59/3= 0,53. В результате средняя длительность полученных комбинаций в расчете на 1 элементарную посылку Т' меньше
Т - заданной длительности элементарной посылки.
Средняя длительность полученных комбинаций будет равна:
Тэф= Нср×Т=0.53×5×10-6=2.65×10-6
Таким образом, средняя длина символа, после статического кодирования, стала меньше.
Найдем производительность источника после кодирования :
Производительность источника при эффективном кодировании
Н'эф(А)= Н(А)/Т = 0.469/2.65×10-6 = 176981.13 = 1.77×105 бит/с.
Полученное значение выше найденного ранее, то есть в результате применения эффективного кодирования повышается производительность источника.
Похожие работы
... символы не равновероятны и зависимы друг от друга, т.е. используется избыточный (помехоустойчивый) код. Избыточность этого кода вычисляется по формуле: . (11) Итак, пропускная способность канала С определяет предельное значение производительности кодера H’(B): H’(B)<C. Отсюда находим предельное значение энтропии кодера: По условию Vk=8*103 сим/с В ...
... обратный процесс - преобразование цифрового сигнала в аналоговый. В данной курсовой работе необходимо рассчитать технические характеристики цифровой системы связи. . 1. СТРУКТУРНАЯ СХЕМА СИСТЕМЫ ЦИФРОВОЙ ПЕРЕДАЧИ НЕПРЕРЫВНЫХ СООБЩЕНИЙ. Для передачи непрерывных сообщений можно воспользоваться дискретным каналом. При этом необходимо преобразовать непрерывное сообщение в цифровой сигнал, то есть в ...
... аппарата будет выглядеть Р 0,6р-0,8-55,8-2К-01-4, его габариты . Вывод Эти простейшие тепловые расчеты двух теплообменных аппаратов одинаковой тепловой производительности показывают, что коэффициент теплопередачи за счет более значительной турбулизации потоков практически в 1,5 раза выше у пластинчатого теплообменника, чем у кожухотрубного. Площадь теплообмена, необходимая для придания
... размеры в верхней части золоотвала, обеспечивающие необходимое осветление воды. Расчет сводится к отысканию объема усеченной пирамиды. В расчете заданы: т=3, L0=96,2 м, Lн=171,0 м. Определим минимальную ширину золоотвала по верху: В0=2(Lн+L0+5)=2(171,0+96,2+5)=544,4 м Объем пирамиды вычисляем по формуле: , W=с0Q24*365Т, где c0 – концентрация пульпы, с0=0,04 т/м3, Q – расход пульпы, Q= ...

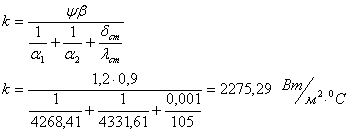
0 комментариев