Навигация
Расчет токов Методом Контурных Токов и Методом Узловых потенциалов
5 Расчет токов Методом Контурных Токов и Методом Узловых потенциалов.
5.1 Расчет токов Методом Контурных Токов.
Суть данного метода заключается в том, что вместо реально действующих токов в ветвях цепи, находят контурные токи. В основе этого метода лежит второй закон Кирхгофа. Однако в отличие от расчета токов по первому и второму Кирхгофа данный метод позволяет сократить количество уравнений.
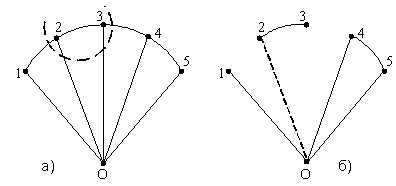
Прежде всего, зададим произвольные направления контурных токов:
Рисунок 5. Положительные направления контурных токов.
Составим систему уравнений по второму закону Кирхгофа, учитывая действующие значения ЭДС:
Для расчета системы уравнений воспользуемся программой - MathCAD 2000 Professional. Распечатка решения приведена в Приложении 2.
Решив систему уравнений, получили следующие контурные токи:
Задав направления токов, как и в решении по законам Кирхгофа (см. рисунок 4), получили следующие значения токов:
5.2 Метод Узловых Потенциалов.
Данный метод основан на первом законе Кирхгофа и на законе Ома. Он позволяет сократить число уравнений.
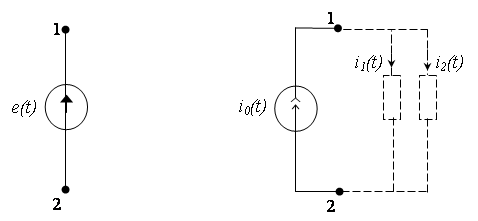
Рисунок 6. Узлы электрической цепи.
Составим уравнения по первому закону Кирхгофа:
Примем за ноль потенциал узла (0) т.е. f0 = 0.
Тогда токи в ветвях, согласно закону Ома:
Где: gk=1/Zk - проводимость, k = 0…6.
Подставив токи в уравнения составленные по первому закону Кирхгофа, получили систему уравнений:
После несложных преобразований система принимает вид:
Система уравнений содержит всего три неизвестных (f1, f2, f3). Для расчета системы уравнений воспользуемся программой - MathCAD 2000 Professional. Распечатка решения приведена в Приложении 3.
Решив систему уравнений и учитывая, что f0 = 0 получили потенциалы:
Воспользовавшись уравнениями для расчета токов, получили:
5.3 Сравнение токов в ветвях цепи.
"Сведём" токи полученные в различных решения в таблицу:
| i | По Кирхгофу | МКТ | МУП |
| 1 | -1,013 + 0,653×j | -1,013 + 0,653×j | -1,013 + 0,653×j |
| 2 | -4,759 + 1,591×j | -4,759 + 1,592×j | -4,754 + 1,591×j |
| 3 | 3,746 - 0,939×j | 3,746 - 0,939×j | 3,746 - 0,939×j |
| 4 | 0,507 - 0,806×j | 0,507 - 0,806×j | 0,507 - 0,806×j |
| 5 | -5,266 + 2,398×j | -5,266 + 2,398×j | -5,266 + 2,398×j |
| 6 | 1,52 - 1,459×j | 1,52 - 1,459×j | 1,52 - 1,459×j |
Таблица 2. Сравнение токов.
Небольшую разницу в значениях токов можно объяснить разной степенью точности вычислений и округлений.
6 Расчет напряжений на пассивных элементах
цепи:
Для расчета напряжений на элементах цепи воспользуемся законом Ома в комплексной форме:
Для нашей схемы получается:
7 Проверка выполнения баланса мощностей.
Условие баланса мгновенных мощностей может быть сформулировано следующим образом: сумма мгновенных мощностей, отдаваемых всеми источниками, равно сумме мгновенных мощностей, потребляемых всеми приемниками энергии.
Проверим выполнение этого условия для нашей схемы:
Учитывая то, что все токи округлены до третьего знака после запятой а также то, что вычисления в MathCAD-е также обладают погрешностью, можно сказать что баланс выполняется.
7 Построение графика изменения комплексного
потенциала.
8 Список использованной литературы:
1. В. П. Попов.
" Основы теории цепей"
Москва, "Высшая школа", 1985г.
2. Г. В. Зевеке, П. А. Ионкин, А. В. Нетушил, С. В. Страхов.
" Основы теории цепей"
Москва, "Энергоатомиздат", 1989г.
3. А. К. Лосев.
" Теория линейных электрических цепей"
Москва, "Высшая школа", 1987г.
Похожие работы
... . 1.2. Если в данный момент времени , это означает, что направление тока в проводнике совпадает с направлением, указанным стрелкой, т. е. положительные заряды перемещаются в направлении стрелки. В теории электрических цепей допускается возможность однозначной, не зависящей от выбора пути, оценки электрических напряжений меду любыми двумя зажимами исследуемой электрической цепи. Это позволяет ...
... Мгновенное напряжение на проводимости G =10 Cм при заданном токе i=12sin(ωt+φ) равно: u=1,2sin(ωt + φ) 4. Электрические цепи при гармоническом воздействии в установившемся режиме Основные свойства линейных цепей: Принципа суперпозиции. Независимыми называют узлы, которые: отличаются одной ветвью. Независимыми называются контура, которые: отличаются одной ...
... любой из ветвей выбранного сечения приводит к связному графу. Отмеченные выше понятия и положения будут использованы в дальнейшем при расчете электрических цепей по методам, вытекающим из законов Кирхгофа. Теорема замещения В теории электрических цепей как при доказательствах ряда ее положений, так и при численных расчетах используется теорема замещения: значения всех напряжений и токов в ...
... неровностей на поверхности анода, т.е. происходит его полировка. 2 Расчётная часть 2.1Задание на курсовую работу Расчет разветвлённой электрической цепи постоянного тока. Для заданной электрической цепи необходимо: 1) Записать систему уравнений по законам Кирхгофа (без расчетов); 2) Определить все токи и ...







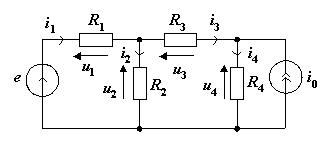
0 комментариев