Навигация
МАТЕМАТИЧЕСКИЙ АППАРАТ ЕСТЕСТВОЗНАНИЯ
44096
знаков
0
таблиц
0
изображений
6. МАТЕМАТИЧЕСКИЙ АППАРАТ ЕСТЕСТВОЗНАНИЯ.
"Тот, кто хочет решать вопросы естественных наук без помощи математики, ставит неразрешимую задачу. Следует измерять то, что измеримо, и делать таковым то, что таковым не является" - сказал выдающийся итальянский физик и астроном Г. Галилей. Законы естествознания отражают количественную взаимосвязь между явлениями. В силу этого они требуют формулировок не только в качественном, но и в количественном виде, т.е. на языке формул.
Математика начинается с простейшего счета (тривиальная арифметика), простейших измерений (обычная геометрия и тригонометрия) и оперирования простыми формулами (алгебра). По мере своего развития естествознание требует все более сложного математического аппарата. Неправые те, кто говорит, что основные законы могут быть сформулированы с использованием только этих операций. Даже введение такого понятия, как скорость или ускорение, не говоря о законах, в которых они используются, уже требует знание раздела высшей математики - дифференциального исчисления. Наиболее сложным разделом естествознания с точки зрения использования математического аппарата для описания теорий и законов является физика. В этом разделе мы введем некоторые определения, которые будут широко использоваться в дальнейшем при описании теорий и законов физики. Конечно, речь пойдет лишь о минимально необходимом математическом аппарате: дифференциальном и интегральном исчислении и векторной алгебре. Всегда нужно помнить, что изучение подавляющего большинства естественнонаучных законов и теорий, как бы ни были они просты на первый взгляд, требует знания специальных разделов высшей математики.
Например, всем известна формулировка закона сохранения заряда - в замкнутой системе алгебраическая сумма зарядов не меняется. Чтобы понять, отражением какого процесса симметрии является этот закон, нам потребовалось бы изучить такие разделы высшей математики, как теория групп, векторный анализ, теорию функций комплексного переменного.
Для успешного усвоения дальнейшего материала читатель должен быть знаком с арифметикой, алгеброй, геометрией, тригонометрией и с началами математического анализа. Нужно хорошо представлять себе, что такое функция, производная, интеграл, и что такое вектор.
Начнем с элементов векторной алгебры. Все изучаемые процессы и явления происходят в окружающем нас трехмерном пространстве. Иногда мы будем абстрагироваться и рассматривать одномерные процессы (например, перемещение вдоль координатной оси). Задать положение тела или материальной точки в пространстве проще всего с помощью декартовой системы координат. Она задается тремя взаимно перпендикулярными осями X, Y и Z как это показано на рис.6.1. Любая точка А может быть задана тремя проекциями на оси координат: Ax, Ay, Az. Если точка А перемещается в пространстве, т.е. ее положение меняется со временем, то меняются и ее проекции на оси. В этом случае они являются функциями времени: x(t), y(t) и z(t). Вектором называется отрезок в пространстве, который имеет длину и направление. В дальнейшем векторы мы будем выделять стрелочкой наверху или жирным шрифтом. Например: A, 
или 
. Модуль (или длину) вектора, которая является скаляром, будем обозначать той же буквой без стрелочки, без выделения шрифтом или под знаком “модуля”: A, B, 
.
В физике положение точки в пространстве принято задавать с помощью специального вектора, который называется радиусом-вектором и обозначается r. Жирный шрифт означает, что мы имеем дело с векторной, а не с скалярной величиной. Так же, как и любой вектор, радиус-вектор определяется длиной r и направлением в пространстве. Радиус-вектор соединяет начало координат с выбранной точкой. Поскольку эта точка может перемещаться с течением времени в пространстве, радиус-вектор также является функцией времени r = r(t). Радиус-вектор можно задать тремя проекциями на координатные оси и ортам. Орт - единичный вектор, направленный вдоль оси координат. Договоримся обозначать орты ex, ey, ez. Так как орты не меняют своего направления в пространстве и их длина всегда равна единице, они являются константами, т.е. не меняются. Проекции радиуса-вектора на оси координат обозначаются либо, как rx(t), ry(t), rz(t), либо просто x(t), y(t), z(t). С учетом введенных обозначений радиус- вектор r(t) записывается:
r(t) = exx(t) + eyy(t) + ezz(t) (6.1)
В случае прямолинейного движения можно одну из осей (например, ось X) направить вдоль направления движения, и написанное выражение сведется к уравнению лишь для одной проекции. Такое движение, задаваемое лишь одним уравнением x = x(t), называется одномерным. Если движение можно задать двумя уравнениями, например, x = x(t) и y = y(t), то такое движение совершается в плоскости (X,Y) и называется двумерным.
Рассмотрим основные действия, которые можно проводить с векторами, в том числе и с радиусом-вектором. Вектора можно складывать и вычитать по правилу параллелограмма или треугольника. Вектор можно умножать на скалярную величину, на число 
. В результате последней операции получится новый вектор, длина которого в больше прежнего. Эти операции легко записываются с использованием (6.1).
r = r1 + r2 = (exx1 + eyy1 + ezz1) + (exx1 + eyy1 + ezz1) =
=ex(x1+x2) + ey(y1 + y2) + ez(z1 + z1) (6.2)
= (exx + eyy + ezz) = exx + eyy + ezz (6.3)
Наряду с описанными, существуют еще операции умножения вектора на вектор. Их две: скалярное и векторное произведение векторов. Из их названий ясно, что результатом скалярного произведения векторов является скаляр, а результатом векторного произведения - вектор. Операция деления на вектор не определена.
Скалярным произведением векторов называется произведение их длин на косинус угла между ними. Скалярное произведение векторов A и B обозначается (AB) или A
B. Если эти векторы заданы в проекциях на координатные оси, то для их скалярного произведения получится выражение:
(AB) = (exAx + eyAy + ezAz) (exBx + eyBy + ezBz) =
= (exex)AxBx + (exey)AxBy + (exez)AxBz +
+ (eyex)AyBx + (eyey)AyBy + (eyez)AyBz +
+ (ezex)AzBx + (ezey)AzBy + (ezez)AzBz =
=AxBx+AyBy+AzBz (6.4).
При выводе (6.4) мы воспользовались тождествами:
(exex) = (eyey) = (ezez) = 1;
(exey)=(eyez)=(ezex)=0 (6.5).
Введем понятие проекции вектора А на вектор В, которую обозначают AB:
.
Соответственно, проекция вектора В на вектор А равна: 
, и для скалярного произведения векторов получим выражение: (АВ) = 
.
Векторным произведением векторов A и B называется вектор С, численно равный произведению модулей векторов A и B на синус угла между ними. Вектор С перпендикулярен обоим векторам, т.е. перпендикулярен плоскости, в которой они лежат. Таких направлений существует два, см. рис.6.3. Из них выбирают одно по правилу правого буравчика: если вращать ручку буравчика от вектора A к вектору B в направлении меньшего угла, то поступательное движение буравчика укажет направление векторного произведения С. Записывается векторное произведение 
или 
. Величина векторного произведения равна 
, т.е. длина отрезка С численно равна площади параллелограмма, образованного отрезками А и B, см. рис.5.3. Таким образом, в окончательном виде получаем:
,
где 
- единичный вектор, перпендикулярный векторам 
и 
.
Векторы, в том числе и радиус-вектор, могут меняться во времени, т.е. они являются функциями времени. Вектор может меняться разными способами. Во-первых, может меняться его длина (модуль) при неизменном направлении вектора в пространстве. Во-вторых, не меняясь по величине вектор может менять свое направление в пространстве. Наконец, вектор может меняться как по длине, так и по направлению. Проекции вектора на оси координат также являются функциями времени, т.е. переменными функциями. Переменные по какому- либо параметру функции могут быть продифференцированы или проинтегрированы по этому параметру. Дифференцирование и интегрирование векторных функций, в принципе, ничем не отличается от дифференцирования и интегрирования скалярных. Дифференцирование или интегрирование вектора можно свести к дифференцированию или интегрированию каждой из его проекций на оси координат. Производная радиуса-вектора по времени записывается в следующем виде:
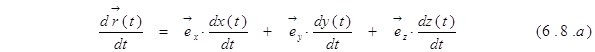. То же самое можно записать в других обозначениях: 
.Здесь и в дальнейшем для удобства и краткости производную по времени будем обозначать точкой над функцией. Приращение (полный дифференциал) радиуса-вектора будет равен:
. Аналогично определяется и операция интегрирования векторной функции:
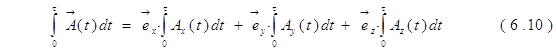.Как видно из (6.8) и (6.10), специфика интегрирования и дифференцирования векторных функций состоит лишь в необходимости проводить эти операции трижды, по разу для каждой проекции.
В некоторых случаях для упрощения описания явления вместо трехмерных векторов рассматривают двумерные и даже одномерные. Это возможно, если движение тела является, к примеру, плоским или прямолинейным. В общем случае такое упрощение описания происходит, если движение тела можно задать менее чем тремя параметрами.
Еще одно понятие, которое нам надо ввести- вероятность. Все знают, что вероятность выпадения “орла” при бросании монеты равна 1/2. Но что это значит? Означает ли это, что при двух бросаниях монеты один раз выпадет “орел” , а второй раз “решка”, или это что-то другое? Введем строгое понятие вероятности, а потом рассмотрим задачу с бросанием монеты.
Пусть у нас имеется система, в которой может реализоваться S какиx-то событий. При бросании монеты S=2. Одно событие - выпадение “орла”, второе - выпадение “решки”. В общем случае число событий может быть любым. Например, при бросании кости имеется 6 событий. Это выпадение одной из 6 цифр от 1 до 6. Мы проводим над системой N измерений. В каждом измерении регистрируем одно из S событий. Пусть N>>S. При измерении i события (i принадлежит множеству s, 1<i<S) мы получили его значение Ni раз. Относительной частотой выпадения i события называется величина Ni/N. Если устремить число измерений (т.е. N)к бесконечности, то относительная частота выпадения события будет равна вероятности выпадения или измерения этого события P(i):
P(i) = lim Ni/N при N -> (6.11).
Значит, если нам известна вероятность выпадения какого-то события, то при очень большом числе измерений N у нас событие i выпадет P(i) N раз. Значит, если мы бросаем монету 1 раз , мы ничего не сможем сказать, какой стороной она упадет. Но, если мы бросаем монету очень много раз (например 10000) то мы можем утверждать, что примерно 5000 раз выпадет “орел”, а 5000 раз- “решка.
Сумма вероятностей выпадения всех событий всегда будет нормирована и равна 1. Действительно, поскольку SNi=N, то имеем: SP(i)= S(Ni/N)=(SNi)/N=1.
Число событий может быть конечно, а может быть и бесконечно. Например, соседние скорости атомов в газе отличаются на бесконечно малую величину. В этом случае вероятность Р будет непрерывной функцией. Для газа, например, это будет функция распределения атомов по скоростям, известная из школьного курса как функция распределения Максвелла.
В заключении этого раздела сделаем акцент на двух моментах.
Первое. Математический аппарат современной физики и всего естествознания в целом огромен и очень сложен. В рамках курса невозможно даже просто перечислить все разделы, которые используются в науке. В этом разделе затронут лишь минимум некоторых разделов математики, необходимых для понимания фундаментальных законов естествознания: алгебры, геометрии, тригонометрии, математического анализа, дифференциального и интегрального исчисления, аналитической геометрии, векторного анализа, теории вероятностей.
Второе. В некоторых учебниках по естествознанию, написанных в основном людьми, не имеющими фундаментальной естественнонаучной подготовки , делаются попытки изложить все естествознание, опираясь на одну только арифметику. Это глубоко ошибочный подход. Без введения понятий переменной величины и функции и соответствующего математического аппарата невозможно не только описать, но даже просто осмыслить тот или иной закон естествознания. Во всех областях естественных и даже общественных наук имеются т. н. "динамические законы", т. е. законы, в которых что-либо меняется. Но даже самый простой динамический параметр скорость, невозможно ввести, не используя языка высшей математики - дифференциального исчисления. Ведь скорость -это производная исследуемой величины по времени.
Похожие работы
... моделирование широко используется там, где экспериментальные исследования трудоемки и дорогостоящи, или вообще невозможны (например, в изучении социальных явлений). Кроме задачи о прогнозе, математическое моделирование помогает классифицировать и систематизировать фактический материал, увидеть существующие связи в мозаике фактов. Это вытекает из того, что модель является специфическим -ярким и ...
... инерциальных системах отсчета. Пространственно-временной континуум – неразрывная связь пространства и времени и их зависимость от системы отсчета. Тема 11. Основные концепции химии 1. Химия как наука, ее предмет и проблемы Важнейшим разделом современного естествознания является химия. Она играет большую роль в решении наиболее актуальных и перспективных проблем современного общества. К ...
... сущность теории химической эволюции и биогенеза. Опишите историю открытия и изучения клетки. Зав. кафедрой -------------------------------------------------- Экзаменационный билет по предмету КОНЦЕПЦИИ СОВРЕМЕННОГО ЕСТЕСТВОЗНАНИЯ Билет № 30 Назовите и охарактеризуйте междисциплинарные естественные науки. Сформулируйте третий закон механического движения Ньютона. Каким ...
... и социальных процессов. Поэтому с целью системного и интенсивного исследования механизма коэволюционного процесса, на современном этапе развития науки необходимо достигнуть органического единства и постоянного взаимовлияния природно-научных и гуманитарных знаний. 4. Современное естествознание характеризуется изменением характера объекта исследования и усилением роли комплексного подхода в его ...
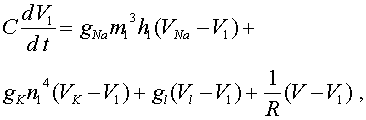
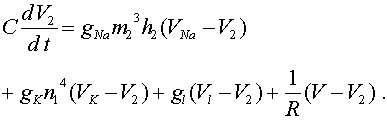
0 комментариев