Навигация
1.3.1 Фический маятник
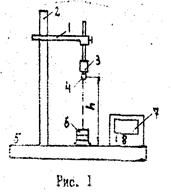
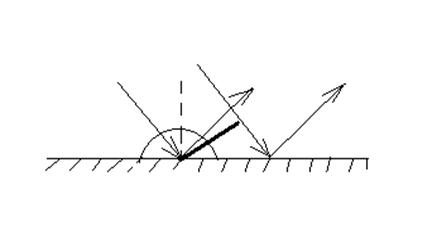
Физический маятник – твердое тело, совершающее под действием силы тяжести колебания вокруг неподвижной горизонтальной оси О подвеса, не проходящей через центр масс С тела (рис.1).
Если маятник отклонен от положения равновесия на некоторый угол, то в соответствии с уравнением динамики вращательного движения твердого тела (e = M/J, где e - угловое ускорение тела, M –момент сил, действующих на тело, J –момент инерции тела относительно оси вращения) момент возвращающей силы F можно записать в виде
(10)
где M = Ftl=-mgl sina =-mgla, J-момент инерции маятника относительно оси, проходящей через точку О, l-расстояние меду точкой подвеса и центром масс маятника С, Ft = -mg sina== -mga – возращающаяся сила и g –ускорение свободного падения.
Уравнение (10) можно записать в виде
(11)
или
(12)
Принимая
(13)
получим уравнение
(14)
решение которого известно как:
(15)
Из выражения (15) следует, что при малых колебаниях физический маятник совершает гармонические колебания с циклической частотой w0 и периодом
(16)
где L=J/(ml) –приведенная длина физического маятника.
Тока О' на продолжении прямой ОС, отстоящая от оси подвеса на расстоянии L, называется центром качаний физического маятника (см. рис.1). Применяя теорему Штейнера, можно показать, что ОО’ всегда больше ОС=l . Точка подвеса О и центр качаний О’ обладают свойством взаимозаменяемости : если ось подвеса сделать проходящей через центр качаний О’, то точка О прежней оси подвеса станет новым центром качаний. При этом период колебаний физического маятника не изменится, а расстояние между точками подвеса будет равно приведенной длине маятника.
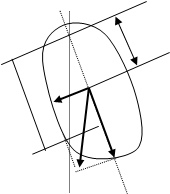
`P=m`g
Рис. 1
1.3.2. Математический маятник
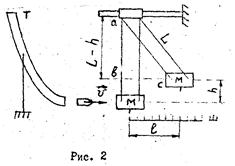
Математический маятник –идеализированная система, состоящая из материальной точки массой m, подвешенной на невесомой нерастяжимой нити, и колеблющаяся под действием силы тяжести.
Момент инерции математического маятника J =ml, где l- длина маятника. Так как математический маятник можно представить как частный случай физического маятника, предположив, что вся масса физического маятника сосредоточена в одной точке – центре масс, то, подставив выражение момента инерции математического маятника в формулу (16), получим известное выражение для малых колебаний математического маятника.
(17)
Сравнивая формулы (16) и (17) видим, что, если приведенная длина физического маятника равна длине математического маятника, то их периоды колебаний одинаковы. Следовательно, приведенная длина физического маятника – это длина такого математического маятника, период колебаний данного физического маятника.
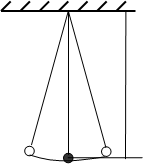
l
m
Рис.2
1.3.3 Оборотный маятник
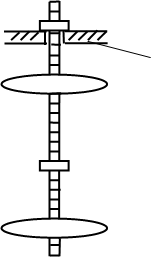
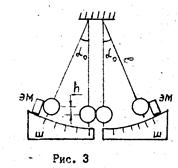
Оборотный маятник является частным случаем физического маятника и состоит из стального стержня 2,двух легких опорных призм 3 и двух массивных грузов 1, имеющих форму чечевиц (рис.3). Призмы и чечевицы могут перемещаться по стержню и фиксироваться с помощью винтов. Если маятник вывести из положения равновесия то он будет совершать колебания в вертикальной плоскости, опираясь нижним ребром одной из призм на закрепленную на массивном штативе опорную площадку 4.
Соотношение T = 2p J/mgl (см. Формулу (16)) может быть использовано для определения ускорения силы тяжести g. Для этого необходимо измерить период колебания маятника T, расстоние l между осью качания и центром масс, определить момент инерции маятника J относительно оси качания и выразить через них g. Оказывается, однако, что с высокой точностью можно измерить только период колебаний Т маятника, а величины l и J достаточно точно определить не удается. Например, для нахождения расстояния l от оси качаний до центра масс маятника необходимо предварительно определить положение центра масс, что сделать точно довольно трудно.
![]() 3
3
4
![]()
1
![]()
![]() 3
3
![]() 1
1
![]()
![]() x
x
![]()
Рис.3
Достоинством метода оборотного маятника для определения ускорения свободного падения является то, что величины J и l не входят в расчетную формулу для g. Перейдем к обсуждению этого метода. Согласно теореме Гюйгенса-Штейнера, момент инерции физического маятника относительно оси качаний О (рис.1)
J = Jc + ml (18)
Где Jc –момент инерции маятника относительно оси, параллельной оси качаний и проходящей через центр масс С маятника, l-расстояние между осью О и центром масс С. Подставляя выражение (18) в (16), получаем
(19)
Обсудим, качественно, характер зависимости периода колебаний от расстояния l между центром масс и осью качаний. При очень малых l момент силы тяжести М=- mgl sina (рис.1), стремящийся вернуть маятник в положение равновесия, становится очень малым и период колебаний резко возрастет. В пределе l ®0, момент силы тяжести равен нулю и колебания вообще невозможны: маятник находится в состоянии раавновесия. Это согласуется с формулой (19): при l ®0 период
(20)
В обратном пределе, для очень больших l , можно пренебречь Jc по сравнению с ml и рассматривать физический маятник как математический с длиной подвеса l. В этом случае период колебаний Т= При l период Т также неограниченно возрастает. При возрастании l период T сначала убывает до некоторого минимального значения Tm=Tmin, а затем вновь возрастает. Качественно вид зависимости T(l) изображен на рис.4.
Значению l=0 соответствует центр масс маятника. Если маятник подвешивать по другую сторону от центра масс, то, как видно из формулы (19), зависимость T(l) будет точно такой же. Поэтому график T(l) имеет две симметричные ветви, соответствующие положению точки подвеса маятника слева или справа от его центра масс.
![]() T
T
 | |||
 | |||
T
![]()
![]()
![]()
![]()
Tm
![]() lm l1 0 lm l2 l
lm l1 0 lm l2 l
Рис.4
Из графика видно, что по каждую сторону от центра масс маятника имеется по две точки подвеса, для которых периоды колебания маятника совпадают.Найдем такие два положения l1 и l2(l2=l1) точек подвеса по разные стороны от центра масс (рис.5), чтобы периоды колебаний маятника совпадали:
T(l1) = T(l2). (21)
Как видно из (19), для этого необходимо выполнение равенстваJc/ml1+l1= Jc/ml2+l2 (22)
которое имеет место либо при l1 = l2, либо при
l2 = Jc/ml1 (23)
В последнем случае период колебаний маятника
(24)
Следовательно, ускорение свободного падения может быть определино по формуле
(24)
Как видно из (24), для нахождения g достаточно измерить только две величины: расстояние L=(l1+l2) между точками подвеса маятника (опорными ребрами призм) и период колебаний маятника в положении l1 и в “перевернутом положении” l2, таком, что l1¹l2. При этом периоды колебаний должны совпадать, т.е. должно выполняться условие T(l1)=T(l2)=T. Напомним, что в этом случае величина L=(l1+l2) называется приведенной длиной маятника.
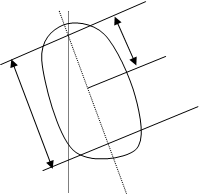
![]()
L
Рис.5
Похожие работы
... , нужно посредством правил подсчета значащих цифр округлить результат математических вычислений так, чтобы точность их соответствовала точности данных, полученных от измерения. ИЗУЧЕНИЕ КИНЕМАТИКИ И ДИНАМИКИ ПОСТУПАТЕЛЬНОГО ДВИЖЕНИЯ НА МАШИНЕ АТВУДА Цель работы Экспериментальная проверка основных уравнений и законов поступательного движения тела на специально сконструированной для этого ...
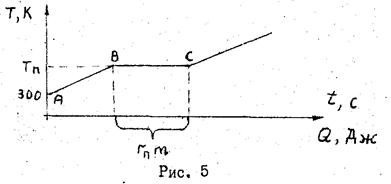
... изменение. 3. Что такое термодинамическая вероятность состояния (статистический вес). 4. Статистический смысл изменения энтропии. 5. Первый закон термодинамики. 6. Вывод рабочей формулы (36) данной работы. 7. Второй закон термодинамики и его статистический смысл. 6. ОПРЕДЕЛЕНИЕ ТЕМПЕРАТУРЫ И УДЕЛЬНОЙ ТЕПЛОТЫ ПЛАВЛЕНИЯ МЕТАЛЛА Цель работы Исследовать фазовый переход первого рода ...
... самопроизвольно протекать не может, необходим подвод энергии извне. 2-й закон термодинамики с использованием понятия энтропии формулируется так: Все процессы в природе протекают в направлении увеличения энтропии, энтропия замкнутой системы не может самопроизвольно уменьшаться. В статистической физике энтропию связывают с термодинамической вероятностью состояния системы – с числом ...
... характеризуют мощностью. Она показыввает, какая работа совершается телом в еденицу времени. Это скорость совершения работы N=A/t. Измеряется в ваттах (за 1 с выполняется работы в 1 Дж). Билет 27 1. 1. Поверхностное натяжение. Смачивание и капиллярность. Поверхностное натяжение в природе и технике. 2. 2. Активное и реактивное сопротивление. Закон Ома для цепи переменного тока. 3. ...


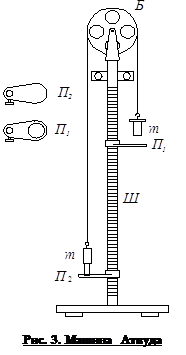

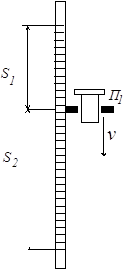






0 комментариев