Кинетическая и потенциальная энергии

1.3. Кинетическая и потенциальная энергии

1.3.1. Кинетическая энергия

 Кинетическая энергия тела является мерой его механического движения и определяется работой, которую необходимо совершить, чтобы вызвать данное движение.

Если сила `F действует на покоящееся тело и вызывает движение со скоростью `v, то она совершает работу, а энергия движущегося тела возрастает на величину затраченной работы. Таким образом, работа силы `F на пути, который тело прошло за время возрастания скорости от 0 до v, идет на увеличение кинетической энергии тела, т.е.

dA=dT (9)

 

Используя скалярную запись второго закона Ньютона и, умножая обе части равенства на перемещение ds, получим

 (10)

Так как  , то

dA=mvdv=dT (11)

и

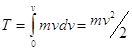(12)

Таким образом, для тела массой m, движущегося со скоростью v, кинетическая энергия системы есть функция состояния движения.

1.3.2. Потенциальная энергия

Потенциальная энергия –часть общей механической энергии системы, определяемая взаимным расположением тел и характером сил взаимодействия между ними.

Пусть взаимодействие тел осуществляется посредством силовых полей ( например, поле упругих сил, поле гравитационных сил), характеризующихся тем, что работа, совершаемая действующими силами при перемещении тела из одного положения в другое, не зависит то того, по какой траектории оно произошло, а зависит только от начального и конечного положений. Такие поля называются потенциальными, а силы, действующие на них – консервативными. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такие силы называются диссипативными (например, сила трения).

Тело, находясь в потенциальном поле сил, обладает потенциальной энергией П. Работа консервативных сил при бесконечно малом изменении конфигурации системы равна убыли потенциальной энергии, так как работа совершается за счет потенциальной энергии:

dA=-dП (13а)

или

(`Fd`r)=-dП (13б)

Следовательно, если известна функция П(r), то из формулы (8б) можно найти силу F.

Потенциальная энергия может быть определена из формулы (8б) как

 (14)

где const –постоянная интегрирования, т.е. потенциальная энергия определяется с точностью до некоторой произвольной постоянной величины. Это, однако, не отражается на физических законах, так как в них входит или разность потенциальных энергий в двух положениях тела, или производная П(`r) по координатам.

Для консервативных сил

(15а)

или в векторном виде

(15б)

где

 (16)

(`i,`j`,k –единичные векторы координатных осей). Вектор, определяемый выражением (16), называется градиентом скаляра П.

Потенциальная энергия тела массой m, поднятого на высоту h над поверхностью Земли, равна

П=mgh (17)

где высота h отсчитывается от нулевого уровня, для которого П0=0, g –ускорение свободного падения.

1.4. Закон сохранения механической энергии

Полная механическая энергия системы –энергия механического движения и взаимодействия:

E=T+П (18)

т.е. равна сумме кинетической и потенциальной энергией.

З-н сохранения энергии – результат обобщения многих экспериментальных данных.Идея этого з-на принадлежит М.В. Ломоносову, изложившему з-н сохранения материи и движения, а количесивенная формулировка з-на сохранения энергии дана намецким врачом Ю.Майером и немецким естествоиспытателем Г.Гельмгольцем.

Для системы материальных точек, на которые кроме внутренних сил взаимодействия действуют внешние силы, можно показать, что работа внешних неконсервативных сил, действующих на систему, равна изменению полной механической энергии системы, т.е.

d(T+П)=dA (19)

При переходе системы из одного состояния 1 в какое-либо состояние 2

(20)

т.е. изменение полной механической системы при переходе из одного состояния в другое равно работе, совершенной при этом внешними неконсервативными силами. Если внешние неконсервативные силы отсутствуют, то из (13) следует, что

d(T+П)=0 (21)

откуда

T+П=E=const (22)

т.е. полная механическая энергия системы тел сохраняется постоянной. Выражение (22) представляет собой закон сохранения полной механической энергии: в системе тел, между которыми действуют только консервативные силы, полная механическая энергия сохраняется, т.е. не изменяется со временем.

Механические системы На тела которых действуют только консервативные силы (внутренние и внешние), называют консервативными системами. З-н сохранения механической энергии можно сформулировать так : в консервативных системах полная механическая энергия сохраняется.

З-н сохранения механической энергии связан с однородностью времени. Однородность времени проявляется в том, что физические з-ны инвариантны относительно выбора начала отсчета времени. Например при свободном падении тела в поле сил тяжести его скорость и пройденный путь зависят лишь от начальной скорости и продолжительности свободного падения тела и не зависят от того, когда тело начало падать.

Существует еще один вид систем – диссипативные системы, в которых механическая энергия постепенно уменьшается за счет преобразования в другие (немеханические) формы энергии. Этот процесс получил название диссипации (или рассеяния) энергии. Строго говоря все системы в природе являются диссипативными.

В консервативных сиcтемах полная механическая энергия остается постоянной. Могут

Происходить лишь превращения кинетической энергии в потенциальную энергию и обратно в эквивалентных количествах так, что полная энергия остается неизменной. Этот з-н есть просто з-н количественного сохранения энергии, а з-н сохранения и превращения энергии, выражающий и качественную сторону взаимного превращения различных форм движения друг в друга. З-н сохранения и превращения энергии – фундаментальный з-н природы, он справедлив как для систем макроскопических тел, так и для систем микротел.

В системе, в которой действуют также неконсервативные силы , например силы трения, полная механическая энергия системы не сохраняется. Следовательно, в этих случаях з-н сохранения механической энергии несправедлив. Однако при “исчезновении” механической энергии всегда возникает эквивалентное количество энергии другого вида. Таким образом, энергия никогда не исчезает и не появляется вновь, она лишь превращается из одного вида в другой. В этом и заключается физическая сущность з-на сохранения и превращения энергии – сущность неуничтожимости материи и ее движения.