Вследствие однородности пространства и времени преобразования должны быть линейными

1. Вследствие однородности пространства и времени преобразования должны быть линейными.

Действительно, если бы производные функций по не были бы константами, а зависели от то и разности , выражающие проекции расстояний между точками 1 и 2 в “движущейся” системе, зависели бы не только от соответствующих проекций , в “неподвижной” системе, но и от значений самих координат что противоречило бы требованию независимости свойств пространства от выбора начальных точек отсчета. Если положить, что проекции расстояний вида x‘ = = зависят только от проекций расстояний в неподвижной системе, т.е. от x = , но не зависит от , то

при т.е. или .

Аналогично можно доказать, что производные по всем другим координатам также равны константам, а следовательно, и вообще все производные по суть константы.

2. Выберем "движущуюся" систему таким образом, чтобы в начальный момент точка, изображающая ее начало координат, т.е. совпадала с точкой, изображающей начало координат "неподвижной" системы, т.е. , а скорость движения системы была бы направлена только по

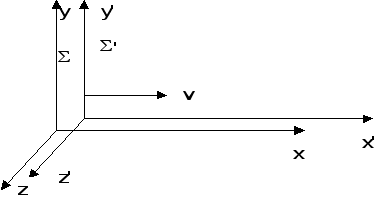Если мы также учтем требование изотропности пространства, то линейные преобразования для системы отсчета , выбранной указанным образом, запишутся в виде Здесь отсутствуют члены, содержащие и в выражениях и , в силу изотропности пространства и наличия единственного выделенного направления вдоль оси , соответственно постановке задачи. На этом же основании в выражениях для и отсутствуют члены, пропорциональные, соответственно, и , а коэффициенты при и одинаковы. Члены, содержащие и , отсутствуют в выражениях для и в силу того, что ось все время совпадает с осью . Последнее было бы невозможно, если бы и зависели от и .

3. Изотропность предполагает также симметричность пространства. В силу же симметрии ничто не должно измениться в формулах преобразования, если изменить знаки и , т.е. одновременно изменить направление оси и направление движения системы . Следовательно, (d) Сравнивая эти уравнения с предыдущими () получаем:

. Вместо удобно ввести другую функцию , так, чтобы выражалось через ипосредством соотношения Согласно этому соотношению, - симметричная функция. Используя это соотношение, преобразования (d) можно записать в виде (e), причем все входящие в эти формулы коэффициенты суть симметрии функции .

4. В силу принципа относительности обе системы, "движущаяся" и "неподвижная", абсолютно эквивалентны, и поэтому обратные преобразования от системы кдолжны быть тождественно прямым от к. Обратные преобразования должны отличаться лишь знаком скорости , т.к. системадвижется относительно системывправо со скоростью , а система движется относительно системы (если последнюю считать неподвижной), влево со скоростью . Следовательно, обратные преобразования должны иметь вид . (f) Сравнивая эти преобразования с (e), получаем . Но в силу симметрии получаем, что , т.е. . Очевидно, имеет смысл лишь знак (+), т.к. знак (-) давал бы при перевернутую по и систему. Следовательно . Замечая, что коэффициенты - тоже симметричные функции , первое и последнее уравнение из (e) и (f) можно записать в виде: А) , а) , В) , в) 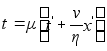. Умножая А) на , В) на и складывая, получим 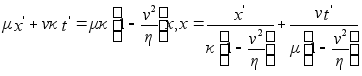. Сравнивая это выражение с а), получаем . 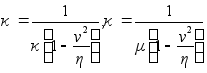Откуда имеем

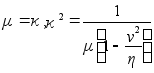
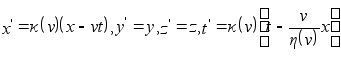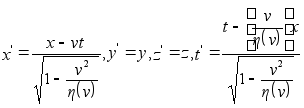Следовательно, извлекая квадратный корень и замечая, что знак (-) так же, как и для , не имеет смысла, получаем . Итак преобразования приобретают вид: (g) или ,подробнее: ,(h) где - неизвестная пока функция .

5. Для определения вида обратимся вновь к принципу относительности. Очевидно, что преобразования (g) должны быть универсальными и применимыми при любых переходах от одних систем к другим. Таким образом, если мы дважды перейдем от системык и от к , то полученные формулы, связывающие координаты и время в системе с координатами и временем в, должны также иметь вид преобразований (g). Это вытекающее из принципа относительности требование, в совокупности с предыдущими требованиями обратимости, симметрии и т.д. означает, что преобразования должны составлять группу.

Воспользуемся этим требованием групповости преобразований. Пусть - скорость системы относительнои - скорость системы относительно системы

Тогда согласно (g)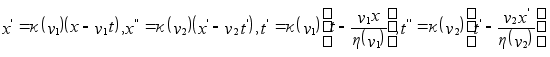

Выражая и через и , получаем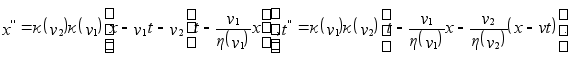

Согласно сформулированному выше требованию эти же преобразования должны записываться в виде (g), т.е. 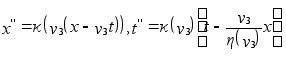(k) Коэффициенты, стоящие при в первой из этих формул и при во второй, одинаковы. Следовательно, в силу тождественности предыдущих формул и этих, должны быть одинаковы и коэффициенты, стоящие при в первой из предыдущих формул и приво второй из формул (h) т.е. 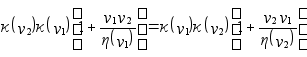. Последнее равенство может быть удовлетворено только при

6. Итак, в преобразованиях (h) h является константой, имеющей размерность квадрата скорости. Величина и даже знак этой константы не могут быть определены без привлечения каких-либо новых допущений, опирающихся на опытные факты.

Если положить , то преобразования (h) превращаются в известные преобразования Галилея Эти преобразования, справедливые в механике малых скоростей (), не могут быть приняты как точные преобразования, справедливые при любых скоростях тел, когда становится заметным изменение массы тел со скоростью. Действительно, учет изменения массы со скоростью приводит к необходимости принять положение об относительности одновременности разобщенных событий. Последнее же несовместимо с преобразованиями Галилея. Таким образом, константа h должна быть выбрана конечной.

Из опыта известно, что при больших скоростях, сравнимых со скоростью света, уравнения механики имеют вид (i), где - собственная масса, совпадающая с массой частицы при малых скоростях (), с - константа, имеющая размерность скорости и числено равная см/сек, т.е. совпадающая со скоростью света в пустоте. Этот опытный факт трактуется как зависимость массы от скорости, если массу определить как отношение импульса тела к его скорости.

Константа имеет такую же размерность, какую имеет h, входящая в формулы преобразования координат и времени (h). Естественно поэтому положить (j), поскольку в экспериментально полученную зависимость массы от скорости не входит никакая иная константа, имеющая квадрата скорости. Принимая это равенство, преобразования (h) записываются в виде 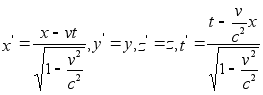(l).

Пуанкаре назвал эти преобразования координат и времени преобразованиями Лоренца.

В силу обратимости обратные преобразования Лоренца, очевидно, должны быть записаны в виде

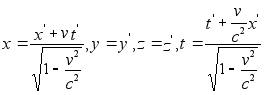
Примененные нами соображения размерности для выбора константы h не вполне, однако, однозначны, т.к. вместо соотношения (j) с таким же правом можно было бы выбрать (k)

Оказывается, однако, что совпадающие с опытом уравнения механики (i) могут быть получены лишь как следствия преобразований Лоренца и не могут быть совмещены с преобразованиями, получающимися из допущения (k). Действительно, известно, что уравнения механики, опирающимися на преобразования Лоренца, являются уравнения Минковского, согласно которым масса увеличивается со скоростью по формуле

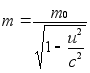. Если же в качестве преобразований координат выбрать 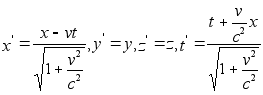, то соответствующие уравнения Минковского дадут убывающую со скоростью массу m, что противоречит опыту.

Итак, не обращаясь к постулату о постоянстве скорости света в пустоте, не ссылаясь на электродинамику и не используя свойств световых сигналов для определения одновременности, мы вывели преобразования Лоренца, используя лишь представление об однородности и изотропности пространства и времени, принцип относительности и формулу зависимости массы от скорости.

Обычно, следуя пути, намеченному еще в первой работе Эйнштейна, вместо формулы зависимости массы от скорости используют постулат о постоянстве скорости света в пустоте. Согласно этому постулату при переходе от системык системедолжно оставаться инвариантным уравнение , описывающее фронт световой волны, распространяющейся из начала координатной системы . Легко убедиться в том, что уравнение после подстановки формул преобразования (k) не изменяет своего вида, т.е. это уравнение переходит в предыдущее, лишь в том случае, если .

Мы применили иной вывод, не использующий постулат о постоянстве скорости света, с тем, чтобы показать, что преобразования Лоренца могут быть получены независимо от способа сигнализации, избранного для синхронизации часов, измеряющих время. Физики могли бы вообще ничего не знать о скорости света и о законах электродинамики, однако могли бы получить преобразования Лоренца, анализирую факт зависимости массы от скорости и исходя из механического принципа относительности.

Таким образом, преобразования Лоренца выражают общие свойства пространства и времени для любых физических процессов. Эти преобразования, как это выяснилось в процессе доказательства, составляют непрерывную группу, называемую группой Лоренца. В этом факте, в наиболее общем виде отображаются свойства пространства и времени, раскрытые теорией относительности.

Изображение преобразований Лоренца на плоскости Минковского.

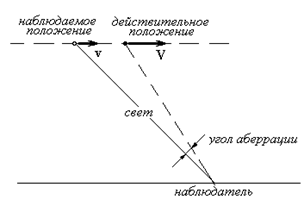
Первыми наиболее поражающими следствиями преобразований Лоренца являются: сокращение движущихся масштабов в направлении движения и замедление хода движущихся часов. С точки зрения повседневных представлений о пространстве и времени эти следствия кажутся парадоксальными.

Исчерпывающее, но всегда кажущееся несколько формальным, разъяснение этих кинематических явлений дается на плоскости x, ct, если в соответствии с правилами четырехмерной геометрии Минковского изобразить на ней сетку координат "неподвижной" и сетку координат "движущейся" системы.

Преобразования Лоренца оставляют инвариантным (неизменным) интервал между любыми двумя событиями, определяемый согласно (a), как в этом легко убедиться подстановкой в (l) в (b).

Совмещая первое событие с моментом t=0 и началом отсчета системы и вводя симметричные обозначения координат и времени интервал между вторым и первым событием можно написать в виде (o) Четырехмерная геометрия, определяемая инвариантностью интервала этого уравнения, качественно отличается от обычной евклидовой геометрии, определяемой инвариантностью расстояния, т.е. (m) или от простого четырехмерного обобщения геометрии, где инвариантом считается (n) В евклидовых геометриях, определяемых (m) или (n), квадрат "расстояния" всегда положителен, и, следовательно, "расстояние" является действительной величиной. Но в четырехмерной геометрии, определяемой интервалом (о), являющимся аналогом "расстояния", квадрат интервала может быть положителен, отрицателен или равным нулю. Соответственно, в этой псевдоевклидовой геометрии интервал может быть действительной или мнимой величиной. В частном случае он может быть равен нулю для несовпадающих событий.

Иногда кажется, что качественное различие между четырехмерной евклидовой геометрией и четырехмерной псевдоевклидовой геометрией стирается, если, воспользовавшись предложением Минковского, считать время пропорциональным некоторой мнимой четвертой координате, т.е. положить

В этом случае квадрат интервала запишется как т.е. с точностью до знака совпадает с (n). Однако в силу мнимости это выражение, так же как и (o), может иметь различные знаки и, таким образом, качественно отличается от (n).

В силу инвариантности интервала качественное различие связи между событиями не зависит от выбора системы отсчета, и действительный, или времениподобный, интервал () остается действительным во всех системах отсчета, мнимый же, или пространственноподобный, интервал () также остается мнимым во всех системах отсчета.

Все эти особенности псевдоевклидовой геометрии могут наглядно проиллюстрированы на плоскости Минковского .

Отрезками 0a и 0b на этой плоскости изображены соответственно единичные масштабы временной оси и пространственной оси . Кривая, выходящая вправо из точки a, является гиперболой, описываемой уравнением а кривая, выходящая вверх из точки b, является гиперболой, описываемой уравнением

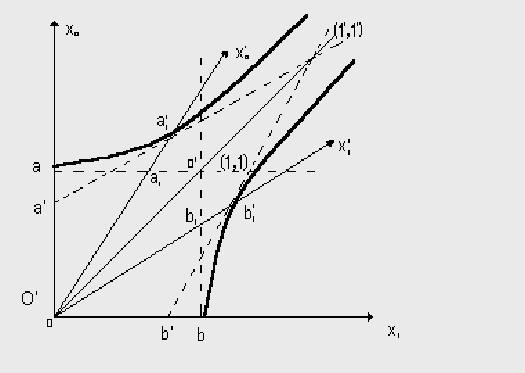
Таким образом, точка начала координат и все точки, лежащие на гиперболе, выходящей из точки a, разделены единичным времениподобным интервалом. Точки же, лежащие на гиперболе, выходящей из точки b, отделены от начала координат пространственноподобным интервалом.

Пунктирная линия, выходящая параллельно оси из точки a, изображает точки с координатами , а линия, выходящая из точки b параллельно оси , изображает точки с координатами .

На этой же плоскости нанесены линии и , изображающие соответственно точки с координатами и , а также линии, проходящие через и

и соответственно изображающие точки с координатами . Эти линии изображают координатную сетку системы .

Из рисунка видно, что переход от системы S к системе соответствует переходу от прямоугольных координат к косоугольным на плоскости Минковского. Последнее следует также непосредственно из преобразований Лоренца, которые можно записать также в ви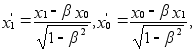де где или в виде (p) где 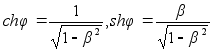и очевидно,

Но преобразования (p) тождественны преобразованиям перехода от декартовых координат к косоугольным. При этих преобразованиях времениподобные векторы, т.е. векторы, направленные из начала отсчета в точки, лежащие выше линии OO', в любой системе координат также останутся времениподобными, т.к. концы векторов лежат на гиперболах. Следовательно, и пространственноподобные векторы во всех системах координат останутся пространственноподобными.

На плоскости Минковского видно, что "пространственная" проекция единичного вектора на ось равна 1, а на ось равна , т.е. меньше 1. Следовательно, масштаб, покоящийся в системе, при измерении из системы S оказался укороченным. Но это утверждение обратимо, ибо "пространственная" проекция вектора Ob на ось равна Ob, т.е. в системе меньше, чем, являющийся единичным вектором.

Аналогично дело обстоит и с "временными" проекциями на оси и Отрезок , изображающий в системе процесс, длящийся единицу времени, в системе S будет проектироваться как , т.е. как процесс, длящийся меньшее время, чем Oa=1. Следовательно, ход часов, покоящихся в системе, при измерении из системы S окажется замедленным. Легко проверить, что это явление также обратимо, т.е. ход часов, покоящихся в системеS, оказывается замедленным в системе.

Сокращение движущихся масштабов.

Если длина неподвижного масштаба может быть измерена путем прикладывания к нему эталонных масштабов, без использования каких-либо часов, то длину движущегося масштаба невозможно измерить из неподвижной системы отсчета без использования часов или сигналов, отмечающих одновременность прохождения концов измеряемого масштаба относительно точек эталона. Таким образом, под длиной движущегося масштаба надо понимать расстояние между его концами, измеренное при помощи неподвижного эталона в один и тот же момент времени для каждого конца. Одновременность измерения положений концов является существенно необходимым условием опыта. Легко видеть, что нарушение этого условия может привести к тому, что измеренная длина может оказаться любой, в том числе отрицательной или равной нулю.

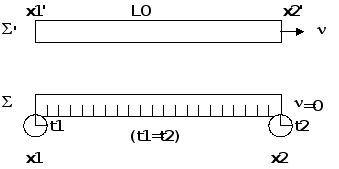Пусть длина движущегося масштаба, предварительно измеренная путем непосредственного приложения к эталону, помещавшемуся в любой системе координат. Тогда если моменты и прохождения концов масштабы мимо точек и неподвижного эталона одинаковы (т.е. t1=t2), то является, по определению, длиной движущегося масштаба. Согласно преобразованиям Лоренца имеем 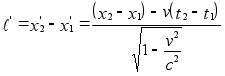, откуда в силу t1=t2 получаем 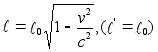.(r)

Парадоксальность этого вывода состоит в том, что в силу принципа относительности точно такая же формула должна получиться для длины масштаба, находящегося в системе S и измеряемого из системы. Иначе говоря, представляется необходимым удовлетворение обратного соотношения 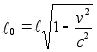, которое находится в явном противоречии с (r), если под и понимать так же измеряемые величины.

Противоречие, однако, снимается, если учесть, что относительность предполагает совершенно симметричное измерение всей системы измерения, т.е. переход от предыдущего рисунка к следующему рисунку: 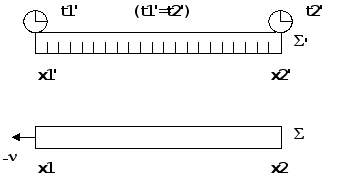В этой схеме уже , но , т.е. концы нижнего масштаба засекаются не в один и тот же момент времени по часам, помещенным в системеS, но в один и тот же момент по часам, находящимся в системе. 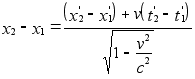Тогда, применяя формулы обратных преобразований Лоренца, получаем , откуда в силу , имеем 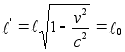. Эта формула действительно означает, что уменьшается длина масштаба , измеренного из системы . Но эта формула уже не находится в противоречии с формулой (r), ибо входящие в нее и измеряются иначе, чем и , входящие в (r).

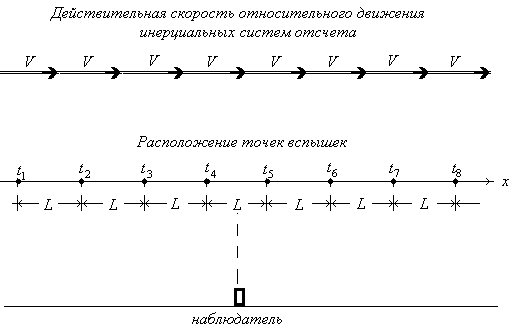
Следовательно, укорочение или удлинение измеряемых масштабов зависит лишь от того, в какой системе отсчета производятся одновременные измерения положений концов масштабов, ибо события, одновременные в одной системе отсчета, неодновременны в другой.

Замедление движущихся часов.

Замедление движущихся часов может быть обнаружено в следующем опыте:

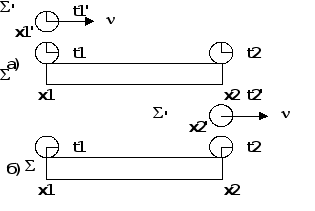Движущиеся со скоростью n часы, измеряющие время , проходят последовательно мимо точки в момент и мимо точкив момент . В эти моменты производится сравнивание положений стрелок движущихся часов и соответствующих неподвижных, находящихся с ними.

Путь за время движения от точки до точки стрелки движущихся часов отмеряют промежуток времени , а стрелки предварительно синхронизированных в неподвижной системе S часов 1 и 2 отмеряют промежуток времени t. Таким образом, (s). Но согласно обратным преобразованиям Лоренца имеем 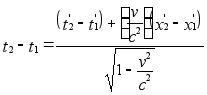. Подставляя (s) в это уравнение и замечая, что движущиеся часы все время находятся в одной и той же точки движущейся системы отсчета, т.е. что , получаем 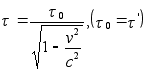.(u)

Эта формула означает, что промежуток времени, отмеченный неподвижными часами, оказывается большим, чем промежуток времени, отмеренный движущимися часами. Но это означает, что движущиеся часы отстают от неподвижных, т.е. их ход замедляется. Эта формула также обратима, как и соответствующая формула для масштабов. Однако написав обратную формулу в виде 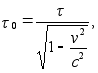(t) мы должны подразумевать, что измеряются уже не в предыдущем опыте, а в следующем: (в этом случае действительно согласно преобразованиям Лоренца )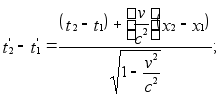

при условии получаем формулу (t). Полученное замедление является вполне реальным, однако оно имеет, так сказать, чисто кинематическую природу. Например, в схеме предыдущего опыта, тот результат, что часы 2 оказались впереди движущихся часов, с точки зрения движущейся системы объясняется тем, что часы 2 с самого начала шли несинхронно с часами 1 и опережали их (в силу неодновременности разобщенных событий, одновременных в другой, движущейся системе отсчета). Таким образом, как замедление движущихся часов, так и сокращение движущихся масштабов не являются парадоксальными, если освоиться с представлением об относительности одновременности пространственно разобщенных событий.

Парадокс часов.

Более поразительным и вызывающим большое число споров и недоразумений является так называемый "парадокс часов". Путь часы А находятся в точке 1 в неподвижной инерциальной системе отсчета S , а одинаковые с ними часы В, находившиеся в начальный момент также в точке 1, движутся к точке 2 со скоростью n. Затем, пройдя путь до точки 2, часы В возвращаются и, приобретая противоположную скорость -n, возвращаются в точку 1

Если время, требуемое на изменение скорости часов В на обратную, достаточно мало по сравнению с временем прямолинейного и равномерного движения от точки 1 до точки 2, то время t, отмеренное часами А, и время , отмеренное часами В, можно вычислить согласно (u) по формулам 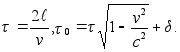(v) где d - возможная малая поправка на время ускоренного движения часов В. Следовательно, часы В, вернувшись в точку 1, реально отстанут от часов А на время Поскольку расстояние может быть сколько угодно большим, постольку поправка d может не приниматься во внимание вообще.

Особенность этого кинетического следствия преобразований Лоренца состоит в том, что здесь отставание хода движущихся часов является вполне реальным эффектом, а не результатом избранной процедуры измерения, как это имело место выше. Реально должны отставать все процессы, связанные с системой, от процессов, идущих в системеS. В том числе должны отставать и биологические процессы организмов, находящихся вместе с часами В. Должны замедляться физиологические процессы в организме человека, путешествующего в системе, в результате чего организм, находившийся в системе в момент ее возврата в точку 1, окажется менее постаревшим, чем организм, оставшийся в системеS.

Парадоксальным представляется здесь то, что один из часов реально отстают от других. Ведь это кажется противоречащим самому принципу относительности, т.к. согласно последнему любую из систем S иможно считать неподвижной. Но тогда представляется, что лишь в зависимости от нашего выбора реально отстающими могут стать любые из часов А и В. Но последнее явно абсурдно, т.к. реально отстают часы В от часов А.

Ошибочность последнего рассуждения состоит в том, что системы S ифизически не равноправны, т.к. система S все время инерциальна, система же некоторый промежуток времени, когда производится изменение ее скорости на обратную, неинерциальна. Следовательно, вторая из формул (v) для системы неправильна, т.к. во время ускорения ход удаленных часов может сильно измениться за счет инерциального гравитационного поля.

Однако и это совершенно правильное объяснение представляется весьма поразительным. Ведь в течении большого промежутка времени обе системы движутся друг относительно друга прямолинейно и равномерно. Поэтому, с точки зрения системы , часы А, находящиеся вS, отстают (но не уходят вперед) в полном соответствии с формулой (v). И лишь за малый промежуток времени, когда в системе действуют инерциальные силы, часы А быстро уходят вперед на промежуток времени, вдвое больший, чем . При этом, чем большее ускорение испытывает система , тем быстрее бежит время на часах А. Наглядно суть полученных выводов может быть разъяснена на плоскости Минковского. 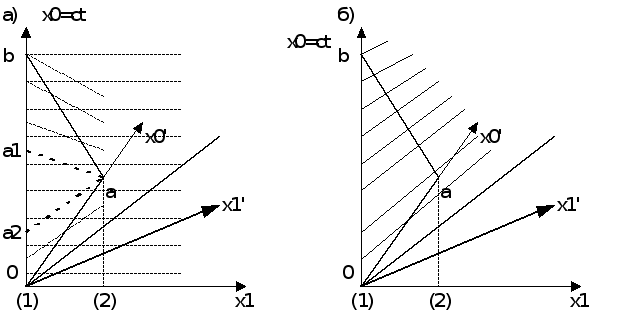Отрезок 0b на этом рисунке изображает покоящиеся часы А, ломаная линия 0ab - движущиеся часы В. В точке a действуют силы, ускоряющие систему часов В и изменяющие ее скорость на обратную. Точки, расставленные на оси 0b, разделяют единичные промежутки времени в неподвижной системеS, связанной с часами А.

Точки на ломаной 0ab отмечают равные единичные промежутки времени, измеряемые часами В, находящимися в системе. Из рисунка видно, что число единичных отрезков, укладывающихся на линии 0b, больше чем число таких же, но относящихся к системе, отрезков, укладывающихся на ломаной 0ab. Следовательно, часы В отстают от часов А. Согласно рисунку "неподвижные" часы А также отстают от часов В вплоть до того момента, изображаемого точкой a. Одновременно с этим моментом является момент a1, однако до тех пор, пока часы В еще движутся со скоростью n. Но через малый промежуток времени, требуемый для замедления часов В и сообщения им скорости -n на часах В практически останется тот же момент a, но одновременным с ним моментом в системеS станет момент a2. То есть, почти мгновенно время системы S как бы перескочит на конечный интервал a1a2.

Этот перескок времени не является, однако, реально наблюдаемым эффектом. Действительно, если из системы S регулярно, через единичные интервалы посылать в систему световые сигналы, то они совершенно регулярно будут приниматься системой S, сперва более редко, а затем, после изменения скорости на обратную, более часто. Никакого разрыва в показаниях часов А в системенаблюдаться не будет. Таким образом, "парадокс часов" также является лишь непривычным для обычных представлений о пространстве и времени следствием псевдоевклидовой геометрии четырехмерного пространственно-временного многообразия.

Список используемой литературы.

1. "Принцип относительности"; Лоренц, Пуанкаре, Эйнштейн, Минковский; ОНТИ., 1935 г.

2. Полное собрание трудов; Л. И. Мандельштам.

3. "Парадоксы теории относительности"; Я. П. Терлецкий; Москва., 1965 г.

4. "Физика пространства-времени"; Э. Ф. Тейлор; Москва., 1963 г.

5. "Общая теория относительности"; Н. В. Мицкевич; Москва., 1927 г.

1 “Принцип относительности” Лоренц, Пуанкаре, Эйнштейн и Минковский; ОНТИ ; 1935 г., стр. 134

2 “Принцип относительности” Лоренц, Пуанкаре, Эйнштейн и Минковский; ОНТИ ; 1935 г., стр. 51

3 Полное собрание трудов, Л. И. Мандельштам; Том 5, стр. 172

4 “Принцип относительности” Лоренц, Пуанкаре, Эйнштейн и Минковский; ОНТИ ; 1935 г., стр. 192

20

План:

1. Происхождение названия “теория относительности” ............................................ стр. 1-2

2. Теория относительности, как современная теория пространства-времени ......... стр. 2-3

3. Постулаты Эйнштейна ............................................................................................... стр. 3-5

4. Вывод преобразрваний Лоренца без постулата о постоянстве скорости света ... стр. 5-9

5. Изображение преобразований Лоренца на плоскости Минковского ............... стр. 10-12

6. Некоторые "парадоксы" теории относительности:

6.а. Сокращение движущихся масштабов ............................................................ стр. 12-13

6.б. Замедление движущихся часов ......................................................................стр. 13-14

6.в. Парадокс часов ................................................................................................. стр. 14-16

7. Список используемой литературы ............................................................................. стр. 16

Похожие работы

Основные представления о специальной и общей теории относительности

Скачать

59336

86

11

... фактами, которые были обнаружены в физике к концу XIX столетия при изучении электромагнитных явлений. Целью настоящей работы является рассмотрение основных представлений о специальной и общей теории относительности, существующих в современной физике. Все рассматриваемые в работе разделы соответствуют основным принципам теории общей и специальной теории относительности. 1 Основные представления ...

К парадоксу близнецов

Скачать

21159

0

0

... время жизни мюона, согласно преобразований Лоренца, должно быть тем больше, чем больше его скорость. Эксперимент подтвердил данный вывод. Как видно из краткого анализа многими авторами рассматривался “парадокс близнецов” и большинство из них придерживаются выводов А. Эйнштейна по этому вопросу, в той или иной форме видоизменяя его. Поэтому в данной статье рассмотрены некоторые вопросы, по теории ...

Аберрация света и парадокс Эренфеста

Скачать

62331

0

3

... . Что касается «сжатия» окружности диска и нарастающего во времени «смещения» друг относительно друга смежных кольцевых слоев диска, то их принципиально не может существовать. У интерпретаторов парадокса Эренфеста не все в порядке со «здравым смыслом». Преобразование Лоренца нельзя применять формально (догматически), не сообразуясь с физикой анализируемых процессов (со здравым смыслом). 6.   ...

Теория относительности

Скачать

60178

0

0

... Вселенной.     5. Проблемы ОТО   5.1 Проблема энергии Так как энергия, с точки зрения математической физики, представляет собой величину, сохраняющуюся из-за однородности времени[53], а в общей теории относительности, в отличие от специальной, вообще говоря, время неоднородно[~ 4], то закон сохранения энергии может быть выражен в ОТО только локально, то есть в ОТО не существует такой ...