Уравнения Максвелла в системе уравнений магнитостатики и электростатики

3. Уравнения Максвелла в системе уравнений магнитостатики и электростатики

Так как на практике почти всегда приходится решать уравнения Максвелла (1) – (4) в кусочно-непрерывных средах, то граничные условия (24) следует рассматривать как неотъёмлемую часть уравнений Максвелла (1) – (4).

В случае стационарных электрических и магнитных полей ( и) система уравнений Максвелла (1) – (4) распадается на систему

уравнений электростатики:

 , ,  (25)

и уравнений магнитостатики:

,  , , (26)

а граничные условия остаются те же.

4. Пример

В качестве примера решения электростатических задач можно вычислить электрическое поле, создаваемое диэлектрическим шаром радиуса R, находящемся в однородном электрическом поле . Уравнения электростатики в диэлектрике (25) при =0 имеют вид:

, ,  (27)

Из этих уравнений следует, сто потенциал электростатического поля удовлетворяет уравнению

   (28)

причём = -, -. В однородном диэлектрике =const , поэтому уравнение (27) переходит в обычное уравнение Лапласа =0.

Граничное условия (24), выражающее непрерывность вектора индукции, записывается следующим образом:

  при r=R (29)

Здесь – решение уравнения вне сферы, а – внутри сферы. Вместо граничного условия непрерывности тангенциальных составляющих электрического поля можно использовать эквивалентное ему условие непрерывности потенциала

= (30)

 

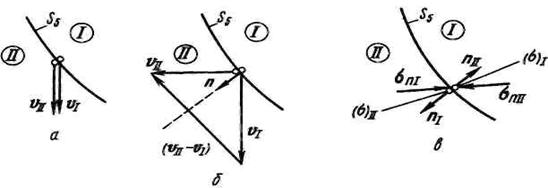
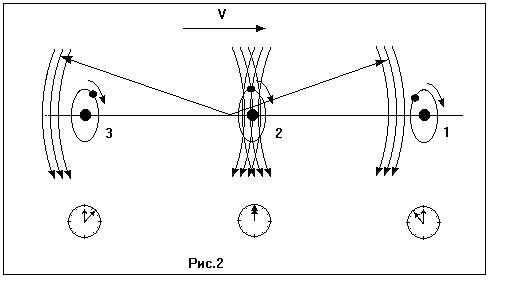
Это условие можно получить, рассматривая интеграл по контуру, изображенному на рис. 2. Воспользовавшись теоремой Стокса и уравнением , находим

Так как интеграл по любому замкнутому контуру равен нулю, то это значит, что функция  непрерывна, откуда и следует условие (30). Из (30) очевидно так же, что

где элемент  направлен касательно к границе раздела. Из этого равенства следует, что тангенциальные компоненты вектора  также непрерывны.

Для решения поставленной задачи используем сферическую систему координат, полярная ось которой (ось z) совпадает с направлением напряжённости однородного внешнего электрического поля .

Поскольку на достаточно большом удалении от диэлектрического шара электрическое поле не искажается наличием этого шара, то потенциал  должен удовлетворять условию

при .

Из соображений симметрии ясно, что потенциал не должен зависеть от азимутального угла, поэтому решение уравнения Лапласа запишем в виде разложения по полиномам Лежандра :

,

.

Здесь потенциал нормирован так, чтобы  при . Так как , то из условия на бесконечности находим .

Воспользуемся теперь граничными условиями (29) и (30):

Приравнивая коэффициенты при одинаковых полиномах Лежандра, получаем

=0 при (l=0),

 при (l=1),

 при (l>1).

Из этих уравнений находим

, .

Все остальные коэффициенты равны нуля, если .

Таким образом, решение задачи имеет вид:

 (30)

Используя формулу , вычислим вектор поляризации диэлектрической сферы

С помощью вектора поляризации формулы (30) можно записать в виде:

 (31)

 (32)

где  - объём сферы.

Первые два слагаемых в (31) и (32) представляют собой потенциал однородного внешнего поля, создаваемого внешними источниками. Вторые – это потенциал электрического поля, создаваемого электрическим шаром, поляризованным внешним полем. Вне сферы – это потенциал диполя с дипольным моментом . Внутри сферы поляризованный шар создаёт однородное электрическое поле с напряжённостью

 (33)

Полная напряжённость внутри шара

(34)

Таким образом, электрическое поле внутри шара не зависят от радиуса шара и ослаблено на значение поля , которое называется деполяризующим полем. Возникновение деполяризующего поля есть частный случай явления экранировки внешнего поля связанными или свободными зарядами.