Навигация
Дисперсионная кривая кристалла
1.1 Дисперсионная кривая кристалла.
Основные черты частотно-углового спектра СПР определяются дисперсионной кривой w (k) кристалла. Дисперсионное соотношение кубического (неанизотропного) кристалла в гармоническом приближении в однорезонансном случае имеет вид:
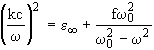 , (2)
, (2)
где e ![]() - диэлектрическая проницаемость среды на частотах много больших фундаментальных частот кристаллической решётки, но много меньших частот электронных переходов, f=e 0-e
- диэлектрическая проницаемость среды на частотах много больших фундаментальных частот кристаллической решётки, но много меньших частот электронных переходов, f=e 0-e ![]() - сила осциллятора, w 0 - фундаментальная частота оптического колебания решетки. На рис.1 приведена дисперсионная кривая соответствующая уравнению (2). Если бы поперечные механические колебания и электромагнитные волны были независимы, то первые описывались
- сила осциллятора, w 0 - фундаментальная частота оптического колебания решетки. На рис.1 приведена дисперсионная кривая соответствующая уравнению (2). Если бы поперечные механические колебания и электромагнитные волны были независимы, то первые описывались
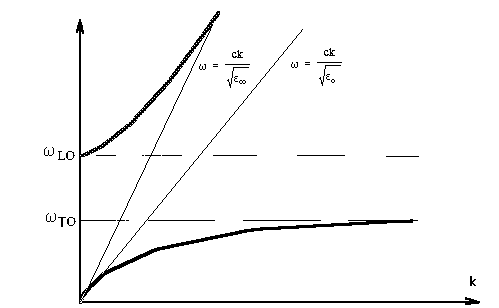
Рис.1 Дисперсия кубического кристалла.
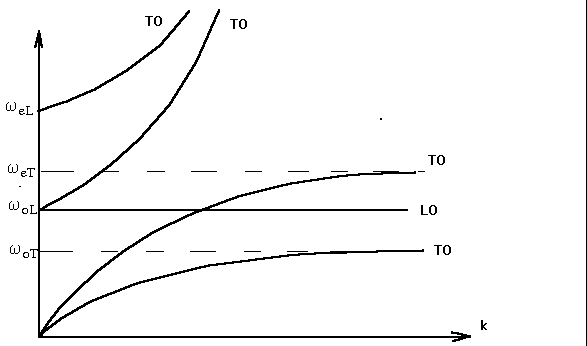
Рис.2 Дисперсия анизотропного кристалла.
бы прямыми .w (k)=w TO и w (k)=w LO, а вторые - прямой w =![]() . Запаздывающее взаимодействие между этими колебаниями в кристалле приводит к поляритонным возбуждениям, имеющим смешанную электромеханическую природу. На частотах, больших w LO находиться верхняя поляритонная ветвь. На частотах между w TO и w LO находится запрещенная зона, где среда не прозрачна для объемных волн.
. Запаздывающее взаимодействие между этими колебаниями в кристалле приводит к поляритонным возбуждениям, имеющим смешанную электромеханическую природу. На частотах, больших w LO находиться верхняя поляритонная ветвь. На частотах между w TO и w LO находится запрещенная зона, где среда не прозрачна для объемных волн.
В анизотропных одноосных кристаллах частотам поперечных и продольных колебаний w Т и w L соответствуют частоты колебаний, смещения которых параллельны (w еТ; w еL) и перпендикулярны (w оТ; w оL) оптической оси. На рис.2 изображены дисперсионные кривые, соответствующие случаю, когда вектор ![]() перпендикулярен главной оптической оси кристалла.
перпендикулярен главной оптической оси кристалла.
1.2. Интенсивность СПР и симметрия кристалла LiNbO3.
Впервые вопрос об интенсивности СПР рассматривался в работе [3]. Когда поляритонная частота w p далека от частоты фонона, достаточно рассматривать квадратичную нелинейную восприимчивость c (2). Будем рассматривать накачку, как плоскую монохроматическую волну с интенсивностью SL и предположим, что углы рассеяния q p,s на частотах w p, w s малы, так что ![]() , где А - сечение рассеивающего объёма V, l - длина кристалла. Тогда мощность, рассеиваемая на частоте w s в направлении
, где А - сечение рассеивающего объёма V, l - длина кристалла. Тогда мощность, рассеиваемая на частоте w s в направлении ![]() в единичный спектральный и угловой интервалы, равна[4]:
в единичный спектральный и угловой интервалы, равна[4]:
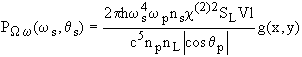 (3)
(3)
где ![]() - свертка тензора c (2) и ортов поляризации соответствующих волн, ns,p,L - показатели преломления на соответствующих частотах, а
- свертка тензора c (2) и ортов поляризации соответствующих волн, ns,p,L - показатели преломления на соответствующих частотах, а 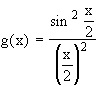 - форм-фактор, описывающий частотно-угловую структуру СПР, когда среда прозрачна на всех трёх частотах. В последнем выражении введено обозначение
- форм-фактор, описывающий частотно-угловую структуру СПР, когда среда прозрачна на всех трёх частотах. В последнем выражении введено обозначение ![]() ,.где
,.где ![]() - отстройка волнового вектора поляритона от точного синхронизма.
- отстройка волнового вектора поляритона от точного синхронизма.
Тензор квадратичной восприимчивости c (2) однородных кристаллов ниобата лития, использовавшихся в данной работе, имеет вид [5]:
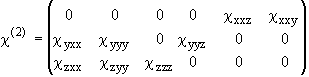 , (4)
, (4)
причём c xxy=-2c yyy, c yxx=-c yyy, c yyz=c xxz, c zyy=c zxx. Кристаллофизические оси ориентированы относительно элементов симметрии следующим образом: ось Z совпадает с оптической осью кристалла, осью симметрии третьего порядка, ось X перпендикулярна плоскости зеркальной симметрии m, а ось Y лежит в этой плоскости. Геометрии рассеяния, которая была реализована в эксперименте, соответствует схематическая запись X(Z,Y)X+D Z. Здесь последовательность индексов задаёт направления векторов ![]() соответственно. Последнее выражение X+D Z определяет плоскость рассеяния, которая, в свою очередь, задается ориентацией входной щели спектрографа (в данном случае плоскость XZ). В соответствии с видом тензора нелинейной поляризуемости (4) константа нелинейного взаимодействия равна:
соответственно. Последнее выражение X+D Z определяет плоскость рассеяния, которая, в свою очередь, задается ориентацией входной щели спектрографа (в данном случае плоскость XZ). В соответствии с видом тензора нелинейной поляризуемости (4) константа нелинейного взаимодействия равна:
![]() (5)
(5)
Это означает, что регистрировалось излучение, рассеянное на обыкновенных поляритонах.
§ 2. Рассеяние света на поляритонах в условиях нелинейной дифракции.
Изменение нелинейной восприимчивости в пространстве оказывает воздействие на протекание параметрического процесса в кристалле. Периодическая модуляция нелинейной восприимчивости влияет на условия пространственного синхронизма[6]:
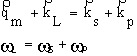 , (6)
, (6)
где ![]() - вектор обратной решётки, связанный со слоями-доменами, d - толщина слоя,
- вектор обратной решётки, связанный со слоями-доменами, d - толщина слоя, ![]() - единичный вектор, перпендикулярный слоям, m - целое число. Условия временного синхронизма при этом не меняются. Эффективная нелинейная восприимчивость (5) может быть разложена в виде(c eff(2)º c ):
- единичный вектор, перпендикулярный слоям, m - целое число. Условия временного синхронизма при этом не меняются. Эффективная нелинейная восприимчивость (5) может быть разложена в виде(c eff(2)º c ):
![]() (7)
(7)
Амплитуды пространственных гармоник квадратичной восприимчивости имеют вид:
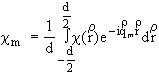 (8)
(8)
Тогда поляризация на частоте рассеянного излучения выглядит следующим образом:
![]() (9)
(9)
Отсюда видно, что интенсивность рассеянного излучения в направлении, соответствующем m-ому порядку дифракции, пропорциональна Фурье-амплитуде c m.
Нелинейная дифракция позволяет получить новое уравнение пространственного синхронизма при генерации второй гармоники. В работе [7] исследовали генерацию второй гармоники (ВГ) в слоисто-неоднородном кристалле ниобата бария-натрия. Была прослежена температурная зависимость интенсивности ВГ при нелинейной дифракции света в окрестности сегнетоэлектрического фазового перехода. Выше температуры этого перехода доменов нет, поэтому интенсивность ВГ резко падает, не опускаясь до нуля, так как существует остаточная поляризованность слоёв.
В работе [6] получены спектры нелинейной дифракции в полидоменном кристалле ниобата бария-натрия при параметрическом рассеянии света. При этом вектор нормали слоёв ![]() был перпендикулярен вектору накачки
был перпендикулярен вектору накачки ![]() . Наблюдалось рассеяние в первом и втором порядке дифракции, смещённого по углу относительно нулевого порядка дифракции. По полученным спектрам определены отклонение направления роста слоёв от оптической оси кристалла и период регулярной доменной структуры .
. Наблюдалось рассеяние в первом и втором порядке дифракции, смещённого по углу относительно нулевого порядка дифракции. По полученным спектрам определены отклонение направления роста слоёв от оптической оси кристалла и период регулярной доменной структуры .
В работе [8] получены одновременно в одном кристалле вторая и третья гармоники излучения 1,064 мкм. При генерации второй гармоники в уравнение волновых векторов входил волновой вектор нелинейной дифракции первого порядка (m=1), а при генерации третьей гармоники - третьего порядка (m=3). Кристалл состоял из участков с периодическими доменами различной толщины. В каждом процессе участвовала область с доменами, толщина которых удовлетворяла уравнению пространственного синхронизма.
§ 3. Экспериментальная установка для наблюдения СПР.
Основными элементами экспериментальной установки (рис.3) для получения спектров спонтанного параметрического рассеяния на поляритонах (ПР-спектрограф) являются: аргоновый лазер (1) с длиной волны l L=488 нм, нелинейный кристалл (6), две призмы Глана (поляризатор (5) и анализатор (6)), трёхлинзовая оптическая система (8) для получения углового спектра и спектрограф (10) для получения частотного спектра.
Излучение лазера после направляющих зеркал (2) проходит через диафрагмы (3); служащие для контроля положения накачки. Далее поляризатор (5) выделяет поляризацию накачки, параллельную щели спектрографа. Анализатор (6) пропускает сигнальную волну с поляризацией, перпендикулярной выделенной поляризации накачки. Интерференционный фильтр (9) задерживает оставшееся излучение накачки.
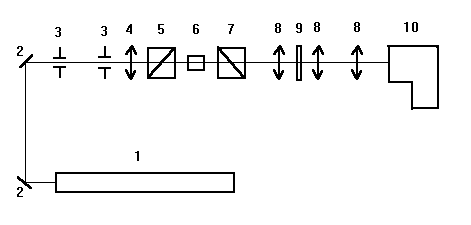
Рис.3. Оптическая схема для наблюдения параметрического рассеяния.
1. Ar+лазер ; 2. Зеркало ; 3. Диафрагма ; 4. Длиннофокусная линза ; 5. Призма Глана (поляризатор) ; 6. Образец (кристалл) ; 7. Призма Глана (анализатор) ; 8. Трехлинзовая система ; 9 Интерференционный фильтр ; 10. Спектрограф.
Глава 2. Исследование характеристик однородных и слоистых кристаллов ниобата лития с различным содержанием примесей методом спектроскопии СПР.
§ 1. Образцы кристаллов LiNbO3.
Исследовались кристаллы ниобата лития с различной концентрацией примесей (Табл.1). Кристалл ниобата лития - одноосный отрицательный в видимой области спектра, имеющий большое двулучепреломление D n=ne-no~ -0.1. Концентрация примесей (Nd и Mg) была измерена с помощью рентгеновского микроанализа. Однородные кристаллы No.4,5,6 выращены вдоль оптической оси Z.
Слоистые кристаллы No.2,3 имели форму параллелепипеда. Примесь неодима практически не влияет на значения показателей преломления. Слои параллельны грани ![]() . Оптическая ось расположена в плоскости ZY под углом 57о к нормали слоев. Кристаллы ниобата лития с вращательными слоями роста и закрепленными на них доменами выращивают путём вытягивания из расплава. В образцах ниобата лития с периодической доменной структурой варьировалась концентрация магния от слоя к слою, соответственно от слоя к слою менялся показатель преломления на малую величину, D n~ 10-4 [10]. Для выращивания монодоменных кристаллов, которые имеют слои с однонаправленным вектором спонтанной поляризации, прикладывают небольшое напряжение к образцу.
. Оптическая ось расположена в плоскости ZY под углом 57о к нормали слоев. Кристаллы ниобата лития с вращательными слоями роста и закрепленными на них доменами выращивают путём вытягивания из расплава. В образцах ниобата лития с периодической доменной структурой варьировалась концентрация магния от слоя к слою, соответственно от слоя к слою менялся показатель преломления на малую величину, D n~ 10-4 [10]. Для выращивания монодоменных кристаллов, которые имеют слои с однонаправленным вектором спонтанной поляризации, прикладывают небольшое напряжение к образцу.
ТАБЛИЦА 1.
| Кристалл LiNbO3 No. | Концентрация магния. NMg ,масс.% | Концентрация неодима. NNd ,масс.% |
| 1 | 0 | 0 |
| 2 | 0.33 | 0.31 |
| 3 | 0.41 | 0.32 |
| 4 | 0.68 | 0 |
| 5 | 0.79 | 0 |
| 6 | 1.04 | 0 |
§ 2 Показатели преломления кристаллов в видимом и инфракрасном
диапазоне спектра излучения.
0 комментариев