Навигация
Расчет углового распределения
3.5. Расчет углового распределения
потока энергии от системы источников
3.5.1. Непрерывное распределение источников
 X
X
b
dx
0 ![]()
DL q ![]()
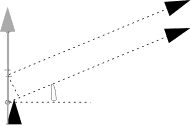
Положение точечного источника определяется его координатой x, амплитуда колебаний пропорциональна dx. Чтобы найти амплитуду колебаний в удаленной от стержня области наблюдения необходимо провести сложение колебаний от всех источников (интегрирование по отрезку 0b):
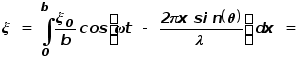
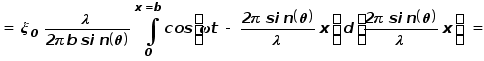
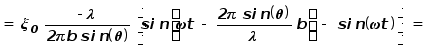
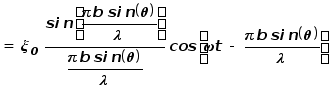 .
.
У нас получилось довольно громоздкое “многоэтажное” выражение, в смысле которого нам надо разобраться. Во-первых, из этого выражения видно, что, как и должно было быть, в некоторой области (точке) наблюдения происходят колебания с частотой w и некоторой начальной фазой. В выражение для амплитуды этих колебаний входит множитель x0. В принципе, он может быть выражен через амплитуду колебаний вблизи стержня с помощью закона сохранения энергии. Но он не представляет для нас особого интереса, как и начальная фаза колебаний. Нужное же нам угловое распределение потока энергии определяется множителем
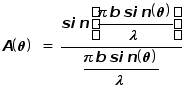 .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() 0 q 0 q 0 q
0 q 0 q 0 q
В числителе
этого выражения
стоит синус
знаменателя.
Поэтому, если
знаменатель
обращается
в нуль при q
= 0, будет
A = 1.
При изменении
q
в пределах ±p/2
величина ![]() периодически
принимает
нулевое значение
и затем достигает
максимумов.
Величина модуля
A
в максимуме
по мере увеличении
модуля q
уменьшается,
поскольку синус
от некоторой
величины изменяется
медленнее, чем
сама эта величина.
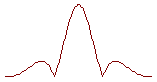
Вид зависимости
периодически
принимает
нулевое значение
и затем достигает
максимумов.
Величина модуля
A
в максимуме
по мере увеличении
модуля q
уменьшается,
поскольку синус
от некоторой
величины изменяется
медленнее, чем
сама эта величина.
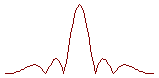
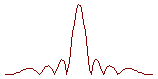
Вид зависимости
![]() при разных
отношениях
b/l
представлен
на рисунке.
при разных
отношениях
b/l
представлен
на рисунке.
3.5.2. Излучение пары точечных источников
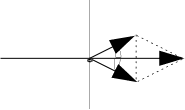
Ранее мы рассматривали суммарные колебания от системы точечных источников в некоторой достаточно удаленной области наблюдения. При этом мы не определяли, по сравнению с чем это удаление велико. Собственно, рассматривая параллельные лучи, мы неявно считали, что область наблюдения находится на бесконечности.
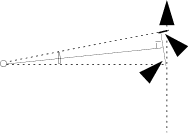
Рассмотрим теперь колебания от уединенного источника в точках плоскости, отстоящей от него на большое, но конечное расстояние l. При этом мы ограничимся небольшим по сравнению с l смещением точки наблюдения от точки падения перпендикуляра, проведенного от источника волн S к плоскости, при малых значениях x.
X
l x
 S q DL
S q DL
xS
l q/2
Проведем от источника волн отрезок прямой в точку наблюдения с координатой x и перпендикуляр к оси координат. Величина xS - это x-координата источника. Мы получили прямоугольный треугольник. Отложим от точки расположения источника вдоль гипотенузы треугольника отрезок длиной l и соединим конец этого отрезка с точкой xS, точкой падения перпендикуляра. Угол при вершине построенного таким образом равнобедренного треугольника
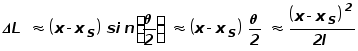 .
.
Соответственно, разность фаз колебаний в этих точках
![]() .
.
В этом
выражении ![]() - разность
x-координат
точки наблюдения
и источника
волн.
- разность
x-координат
точки наблюдения
и источника
волн.
 X
X
x
S’
d 0
S”
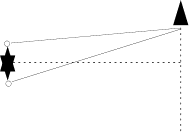
Полученное выражение является для нас вспомогательным. Применим его для решения задачи об амплитуде колебаний, созданных двумя точечными источниками, расположенными на расстоянии d друг от друга и на расстоянии l от плоскости наблюдения.
Разность фаз колебаний, созданных нашими источниками в точке x,
![]() .
.
В круглых скобках записаны разности x-координат точки наблюдения и источников волн. После возведения в квадрат мы получаем:
 Dj
Dj
x
x0
![]() .
.
Произведем сложение этих колебаний с помощью векторной диаграммы. Фаза результирующих колебаний нас не интересует, а амплитуда
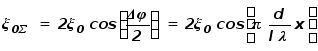
принимает максимальные значения 2x0 в точках, отстоящих друг от друга на
![]()
(при изменении аргумента косинуса на p). Центральный максимум наблюдается при x = 0.
Похожие работы
... основ и ясно поставленных целей, обучение зачастую сводится к передаче знаний посредством бессистемных методов и приемов. Перестройка школы, совершенствование учебно-воспитательного процесса требуют от учителя особое внимание уделять развитию критического мышления учащихся. [3] 1.3 Физика как основа для развития критического мышления Безусловно, этот процесс должен быть комплексным, т.е. ...
... приборы (рычажные весы, электроскоп и др.); -работы, выполняемые на приборах, выпускаемых промышленностью. Классификация взята из [1]. В своей книге [2] С.Ф. Покровский показал, что домашние опыты и наблюдения по физике, проводимые самими учащимися: 1)дают возможность нашей школе расширить область связи теории с практикой; 2)развивают у учащихся интерес к физике и технике; 3)будят ...
... пользователя: VI—XI классы. Платформа: Windows. Носитель: компакт-диск. Варианты построения уроков с использованием электронного учебника 1. Электронный учебник используется при изучении нового материала и его закреплении (20 мин. работы за компьютером). Учащихся сначала опрашивают по традиционной методике или с помощью печатных текстов. При переходе к изучению нового материала ...
... значениями этих параметров, чтобы определить предельные значения и шаг расчёта рассчитываемых параметров. Заключение Хочется выразить уверенность, что в следующих версиях курса "Открытая физика" количество компьютерных моделей будет расти, их функциональные возможности станут разнообразнее, а пределы изменения числовых значений параметров, описывающих эксперименты, будут расширены. Надеемся, что ...

0 комментариев