Навигация
Закон Джоуля-Ленца.
Если проводник неподвижен и в нём не протекают химические реакции, то работа тока идёт на увеличение внутренней энергии проводника, в результате чего проводник нагревается.
Количество тепла определяется по формуле:
![]() , где
, где
![]()
Отсюда:
![]() (47)
(47)
Это закон Джоуля-Ленца в интегральной форме.
Если сила тока изменяется во времени, то количество тепла определяется по формуле:
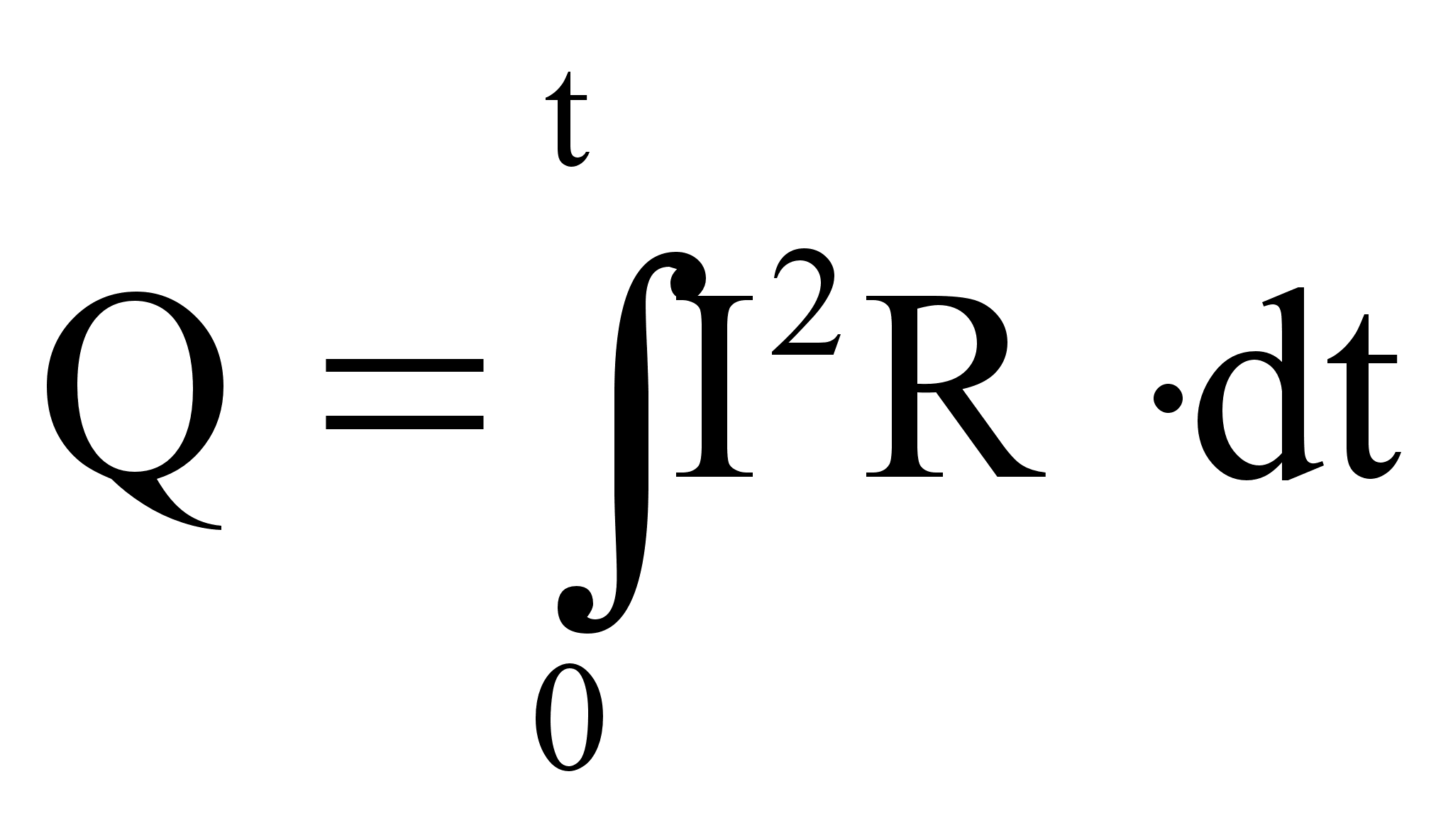 (48)
(48)
Используя закон Джоуля-Ленца можно перейти к выражению, характеризующему выделение тепла в различных физически элементарных объёмах проводника.
Выделив в проводнике элементарный объём в видже цилиндра:
(Рисунок)
![]()
Здесь ![]() ,
,
![]() ,
,
![]()
![]()
Разделив
полученное
уравнение на
![]() и
и
![]() ,
получим формулу
удельной тепловой
мощности
электрического
тока:
,
получим формулу
удельной тепловой
мощности
электрического
тока:
![]() (49)
(49)
Обе полученные формулы закона Джоуля-Ленца справедливы и для неоднородного участка цепи, если сторонние силы имеют не химическое происхождение.
Электрический ток в газах.
Прохождение электрического тока через газ называется газовым разрядом. Газ проводит ток в том случае, если некоторая часть его молекул ионизируется, то есть нейтральный атом расщепляется на положительный ион и свободный электрон. При этом совершается работа противоположных сил электростатического притяжения со стороны положительного ядра и электрона. Такая работа называется – энергией ионизации.
Для газа:
![]()
Закон Ома для неоднородного участка цепи.
На неоднородном
участке цепи
на носители
тока действует
электростатические
силы ![]() и сторонние
силы
и сторонние
силы
![]() .
Следовательно,
плотность тока
.
Следовательно,
плотность тока
![]() в этих точках
оказывается
пропорциональной
сумме напряжений:
в этих точках
оказывается
пропорциональной
сумме напряжений:
![]() (41)
(41)
Выражение (41) представляет собой закон Ома для неоднородного участка цепи в дифференциальном виде.
Перейдём к интегральной форме закона Ома. Рассмотрим неоднородный участок цепи. В следствие закона сохранения электрического заряда, сила тока в любом сечении проводника будет постоянной.
(Рисунок)
![]()
Подставим
в (41) значения
![]() и
и
![]() .
Получим выражение
для элементарного
участка цепи:
.
Получим выражение
для элементарного
участка цепи:
![]()
![]() ,
,
где ![]() и
и
![]() - проекции на
элемент контура
- проекции на
элемент контура
![]() .
.
Умножим
последнее
соотношение
на модуль ![]() и проинтегрируем
по контуру:
и проинтегрируем
по контуру:
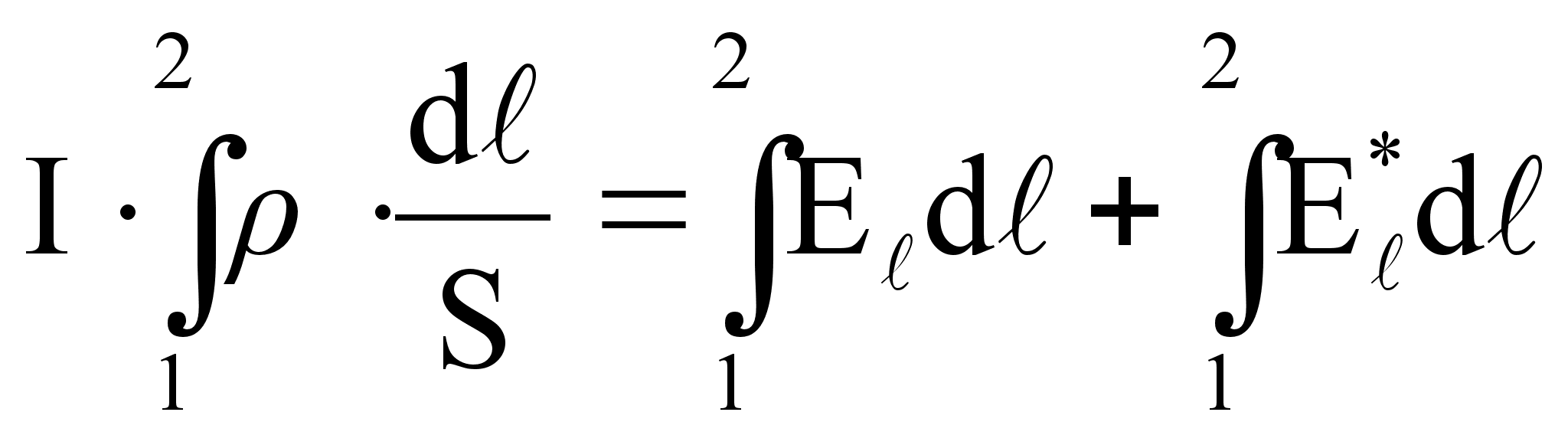 .
.
Учитывая,
что 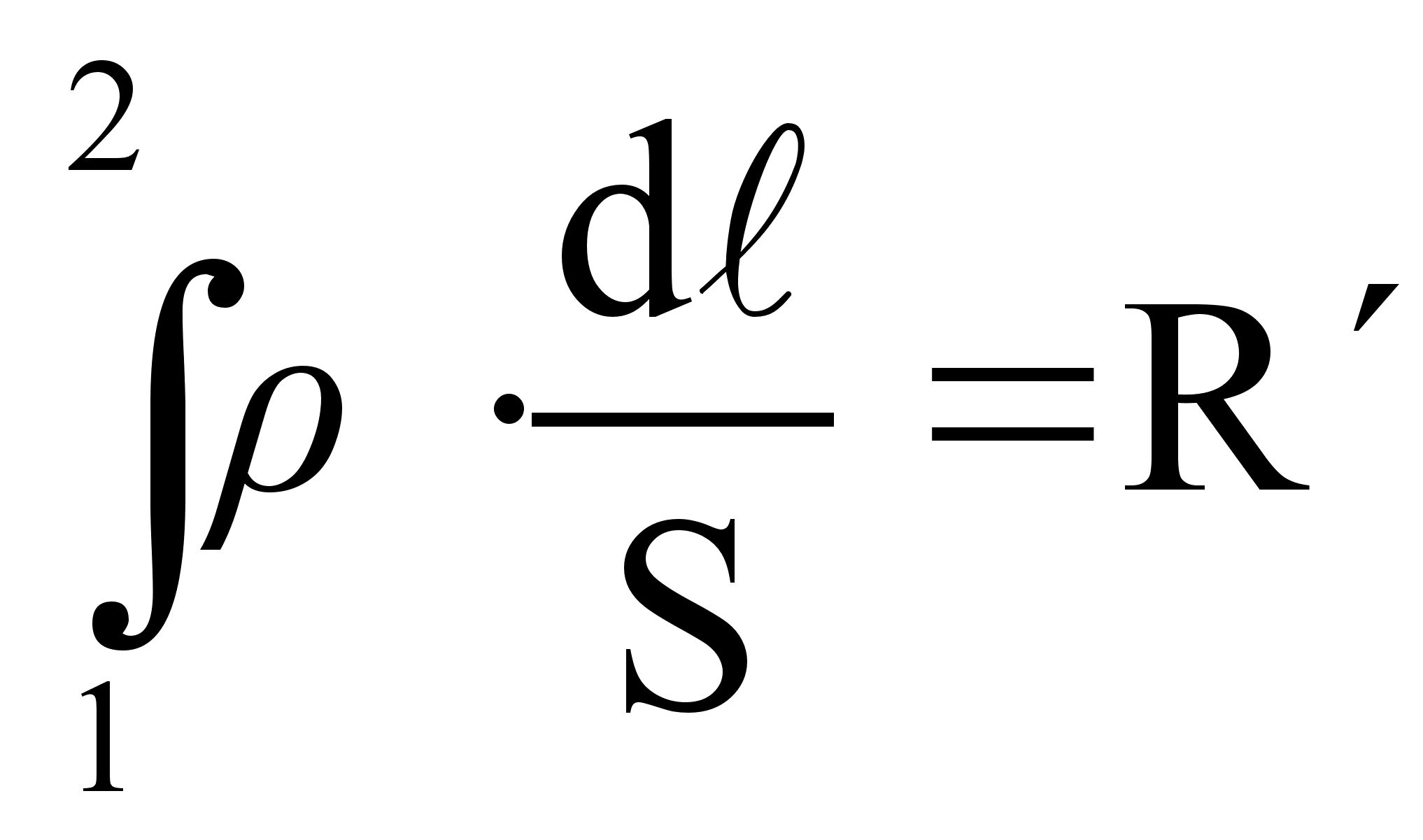 - сопротивление
участка цепи
1-2,
- сопротивление
участка цепи
1-2, 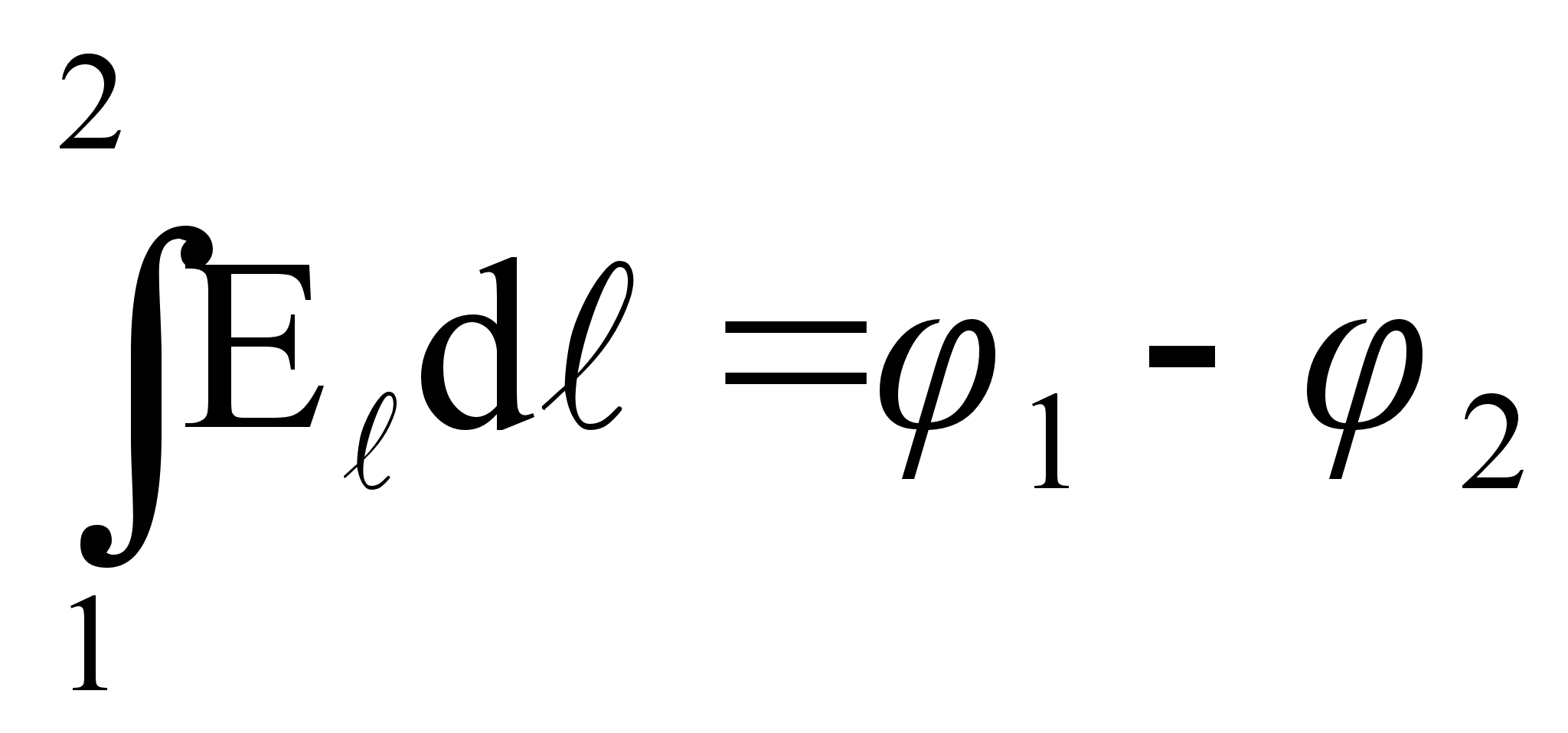 ,
,
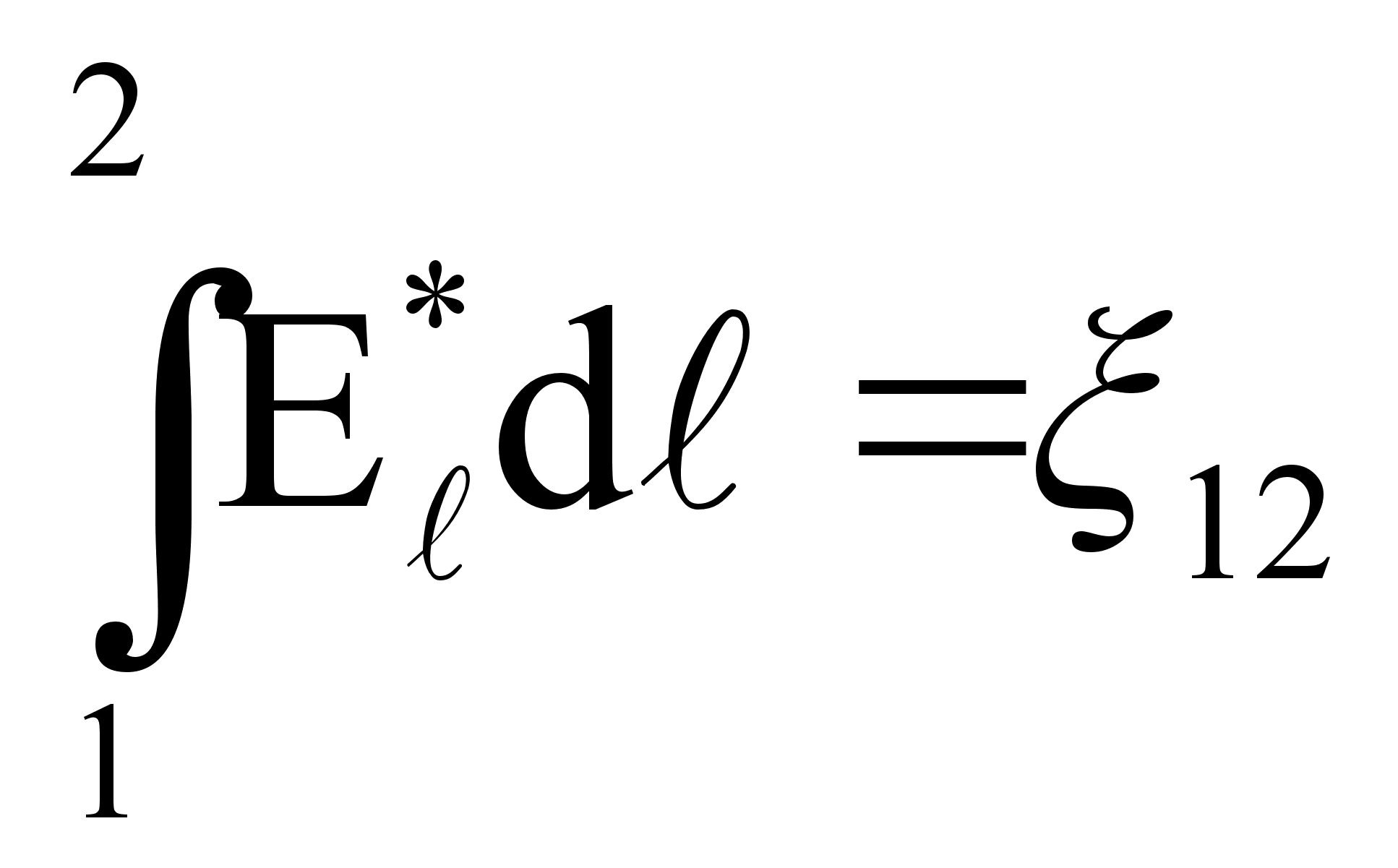 , получим:
, получим:
![]() .
.
Если ![]() - способствует
движению
положительных
зарядов в выбранном
направлении,
то
- способствует
движению
положительных
зарядов в выбранном
направлении,
то
![]() .
.
Если нет, то
![]() .
.
Запишем последнее соотношение в виде:
![]() (42)
(42)
(42) представляет собой закон Ома для неоднородного участка цепи в интегральной форме.
Для замкнутой
цепи ![]() :
:
(Рисунок)
![]() ( 43)
( 43)
Это закон Ома для замкнутого неоднородного у4частка цепи в интегральной форме.
Здесь ![]() ,
где R –
внешнее
сопротивление
цепи,
,
где R –
внешнее
сопротивление
цепи,
![]() - сопротивление
источника ЭДС.
- сопротивление
источника ЭДС.
Закон Ома для однородного участка цепи.
Сопротивление проводников.
Сила тока, текущего по однородному металлическому проводнику пропорциональна напряжению и обратно пропорциональна сопротивлению проводника. ![]() (38)
(38)
где ![]() -
сопротивление.
-
сопротивление.
![]() .
.
![]() - сопротивление
такого проводника,
в котором при
напряжении
1В течёт ток
силой 1А.
- сопротивление
такого проводника,
в котором при
напряжении
1В течёт ток
силой 1А.
![]() - электропроводимость.
- электропроводимость.
Сопротивление проводника определяется по формуле:
![]() (39)
(39)
где![]() - удельное
сопротивление.
- удельное
сопротивление.
Если подставить (39) в (38), то получим:
![]() ;
; ![]()
Учитывая,
что
![]() - плотность
тока,
- плотность
тока,
![]() -
удельная
электрическая
проводимость,
-
удельная
электрическая
проводимость,
![]() - напряжённость
электрического
поля в проводнике,
- напряжённость
электрического
поля в проводнике,
получим
![]() (40)
(40)
Выражение (40) представляет собой закон Ома в дифференциальной форме.
Для большинства металлов при температурах, близких к комнатным:
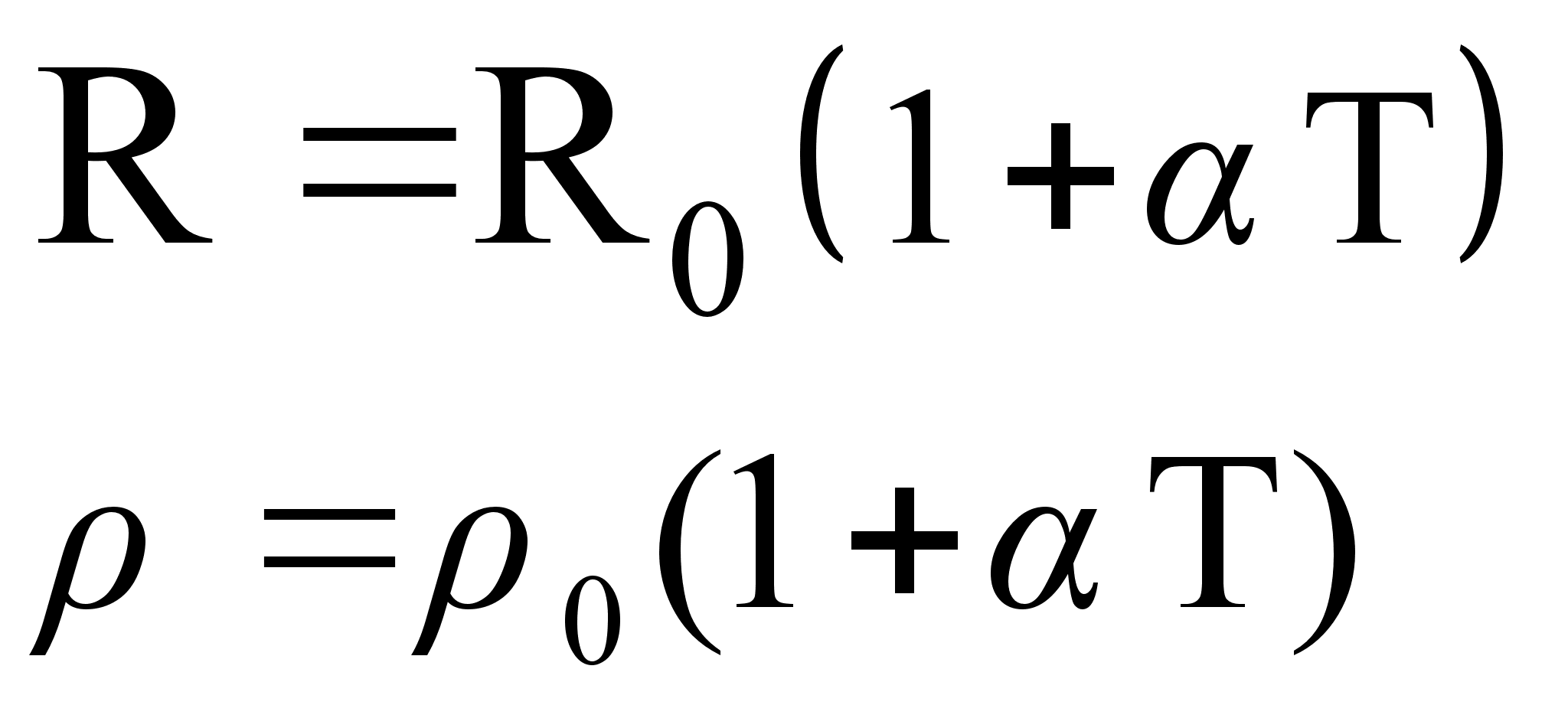
где ![]() и
и
![]() -
сопротивление
и удельное
сопротивление
при
-
сопротивление
и удельное
сопротивление
при ![]() ,
,
![]() - температурный
коэффициент.
- температурный
коэффициент.
(Рисунок)
![]() - при последовательном
соединении
проводников.
- при последовательном
соединении
проводников.
(Рисунок)
При параллельном соединении:
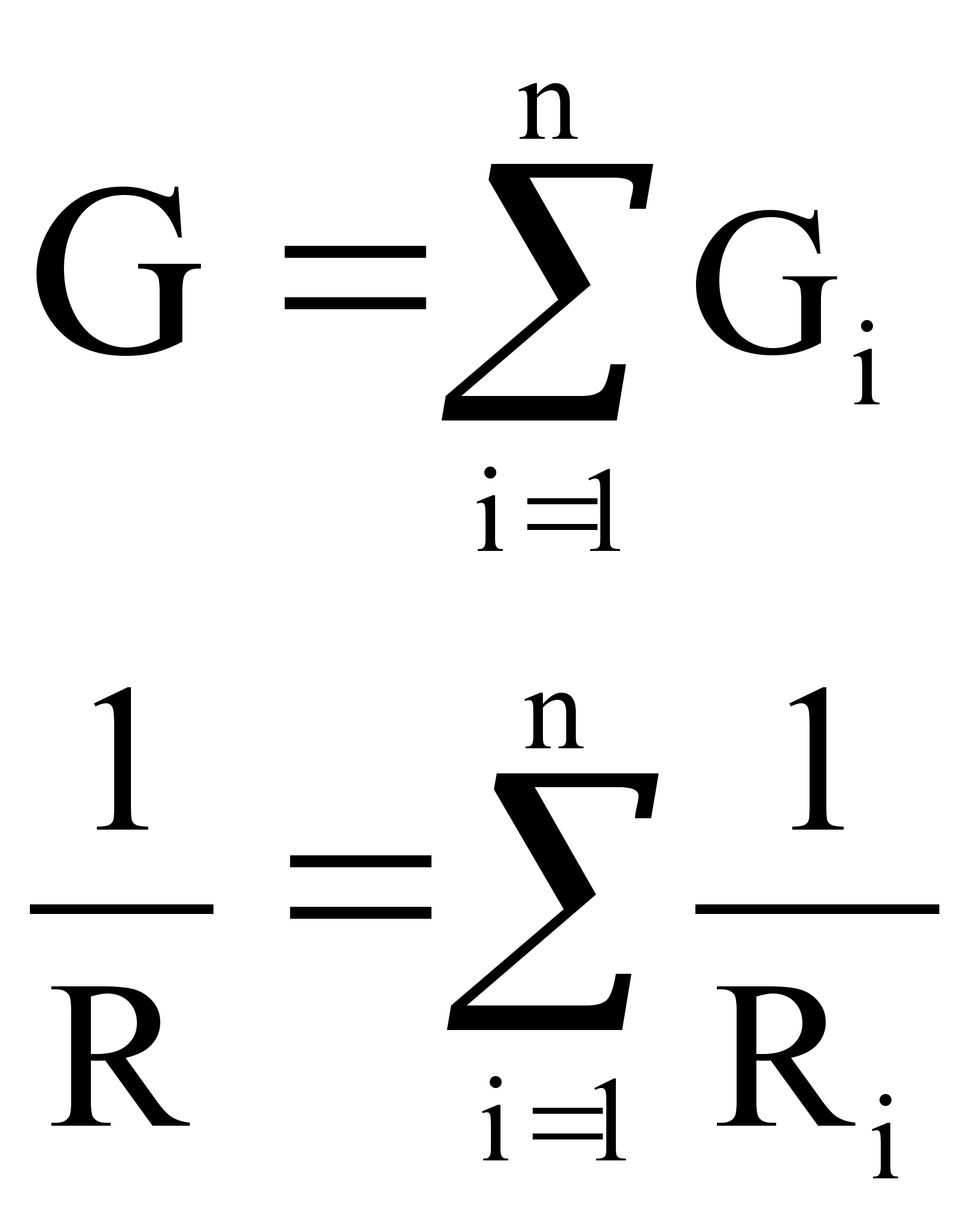
Температурную
зависимость
проводников
используют
для измерения
температур
с высокой точностью
(до ![]() ).
).
Мощность тока.
За время t через поперечное сечение проводника произвольного участка цепи проходит заряд.
![]() - это ??????? тому, что
заряд
- это ??????? тому, что
заряд ![]() переносится
за время из
одного конца
проводника
в другой. При
этом илы
электростатического
поля и сторонние
силы совершают
работу:
переносится
за время из
одного конца
проводника
в другой. При
этом илы
электростатического
поля и сторонние
силы совершают
работу:
![]() (44)
(44)
где U – напряжение на участке цепи.
Учитывая,
что ![]() ,
запишем интегральное
выражение для
мощности тока:
,
запишем интегральное
выражение для
мощности тока:
![]() (45)
(45)
Эта мощность может расходоваться на совершение рассматриваемыми участками цепи работы над внешними телами (если участок перемещается в пространстве), на протекание реакций, на нагревание другого участка цепи.
Удельная
мощность –
мощность, развиваемая
в единице объёма
проводника.
С другой стороны
сила ![]() развивает при
движении единичного
носителя тока
развивает при
движении единичного
носителя тока
![]() усреднённую
мощность:
усреднённую
мощность:
![]() ,
где
,
где
![]() - средняя скорость
упорядоченного
движения носителей
зарядов.
- средняя скорость
упорядоченного
движения носителей
зарядов.
Мощность
![]() можно
найти, умножая
можно
найти, умножая
![]() на
на
![]() (n
– концентрация
носителей
зарядов), таким
образом получаем:
(n
– концентрация
носителей
зарядов), таким
образом получаем:
![]()
где
![]() .
.
Отсюда:
![]() (46)
(46)
(46) представляет собой дифференцированное выражение для мощности тока.
Постоянный электрический ток.
Электродинамика рассматривает явления и процессы, обусловленные движением электрических зарядов.
Электрический ток.
Если через некоторую площадку переносится суммарный заряд, отличный от нуля, то через эту площадку течёт электрический ток.
(Рисунок)
Он возникает в том случае, если в проводнике поддерживается электрическое поле Е, которое перемещает носители тока (электроны, ионы, заряженные пылинки, капельки и т.д.).
Носитель заряда участвуют в тепловом (хаотическом) движении.
(Рисунок)
При включении
поля на хаотическое
движение носителей
накладывается
упорядоченное
движение ![]() .
.
Таким образом, электрический ток – это любое упорядоченное движение электрических зарядов.
За направление тока принимают движение положительных зарядов, то есть ток течёт от плюса к минусу. Количественной мерой тока служит сила тока (I) – скалярная величина, определяющаяся электрическим зарядом, проходящим через поперечное сечение проводника в единицу времени.
![]()
Для постоянного тока, то есть тока не изменяющегося во времени:
![]() ,
, ![]() .
.
Если электрический ток создаётся носителями обоих знаков, движущихся в противоположных направлениях, то:
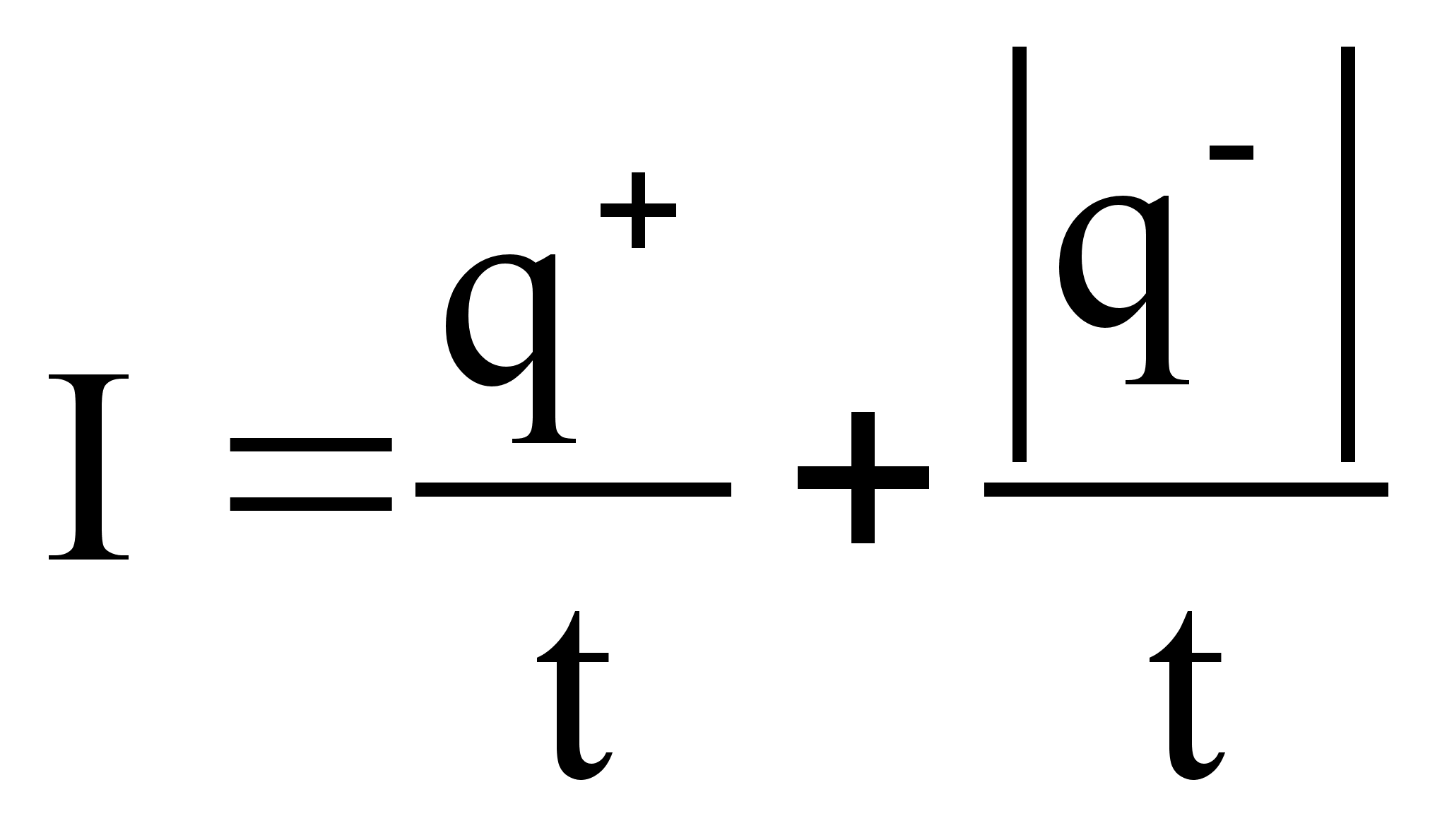
Таким образом, сила тока представляет собой поток заряда через поверхность. Электрический ток может быть неравномерно распределён по поверхности площадки, через которую он протекает, поэтому для детальной характеристики тока используют понятие плотности тока – это векторная физическая величина, определяемая силой тока, проходящей через единичную площадку, перпендикулярную направлению движения носителей:
![]() ,
где
,
где ![]() - направление
нормали.
- направление
нормали.
За направление вектора ![]() принимается
направление
вектора средней
скорости
положительных
зарядов. Зная
вектор плотности
тока в любой
точке пространства,
можно найти
силу тока через
любую поверхность
S:
принимается
направление
вектора средней
скорости
положительных
зарядов. Зная
вектор плотности
тока в любой
точке пространства,
можно найти
силу тока через
любую поверхность
S:
![]()
То есть сила тока – это поток вектора плотности тока через поверхность.
Уравнение непрерывности.
Рассмотрим некоторую замкнутую поверхность, через которую протекает электрический ток. Поток вектора плотности через эту поверхность в единицу времени будет равен скорости убывания заряда.
![]()
(Рисунок)
Учитывая,
что ![]() (интеграл
от плотности
заряда), получим
соотношение:
(интеграл
от плотности
заряда), получим
соотношение:
![]() .
.
Перейдём к частным производным, так как плотнасть заряда в общем случае зависит и от времени, и от координат:
![]()
Преобразуем левую часть выражения по теореме Гаусса:
![]() .
.
Интегралы равны, значит равны и подынтегральные выражения:
![]() (36)
(36)
Выражение
(36) – уравнение
непрерывности.
Оно выражает
закон сохранения
электрического
заряда. В случае
стационарного
(постоянного
тока) производная
по времени
равна нулю,
следовательно,
![]() .
То есть в случае
постоянного
тока вектор
плотности не
имеет источников,
значит, линии
тока нигде не
начинаются,
нигде не заканчиваются
(они замкнуты).
.
То есть в случае
постоянного
тока вектор
плотности не
имеет источников,
значит, линии
тока нигде не
начинаются,
нигде не заканчиваются
(они замкнуты).
Правила знаков.
Если направление тока совпадает с выбранным направлением обхода, то знак положительный. В противном случае – отрицательный.
ЭДС берём со знаком «+», если в направлении обхода внутри источника тока идём от минуса к плюсу и наоборот, ЭДС имеет отрицательный знак, если идём от плюса к минусу.
Следует иметь ввиду, ???????????????????????, которые нельзя получить наложением других контуров друг на друга. Например, можно закончить второе правило Кирхгофа:
(Рисунок)
для контура 1-2-3-6-1
?????????7
Значит, контур находился наложением первых двух. В качестве независимых следует взять любые два контура из трёх, направление обхода в каждом отдельно взятом контуре можно выбирать совершенно произвольно.
Недостающие уравнения составляют, используя первое правило Кирхгофа. Таким образом, число независимых уравнений, составленных в соответствии с первым и вторым правилами Кирхгофа, оказывается равным числу различных токов, текущих в разветвлённой цепи.
Правила Кирхгофа.
Узлом называется точка, в которой сходятся три и более проводника.
I правило: Алгебраическая сумма токов, сходящихся в узле, равна нулю.
(Рисунок)
![]()
II правило: Алгебраическая сумма напряжений в замкнутой цепи равна алгебраической сумме ЭДС.
(Рисунок)
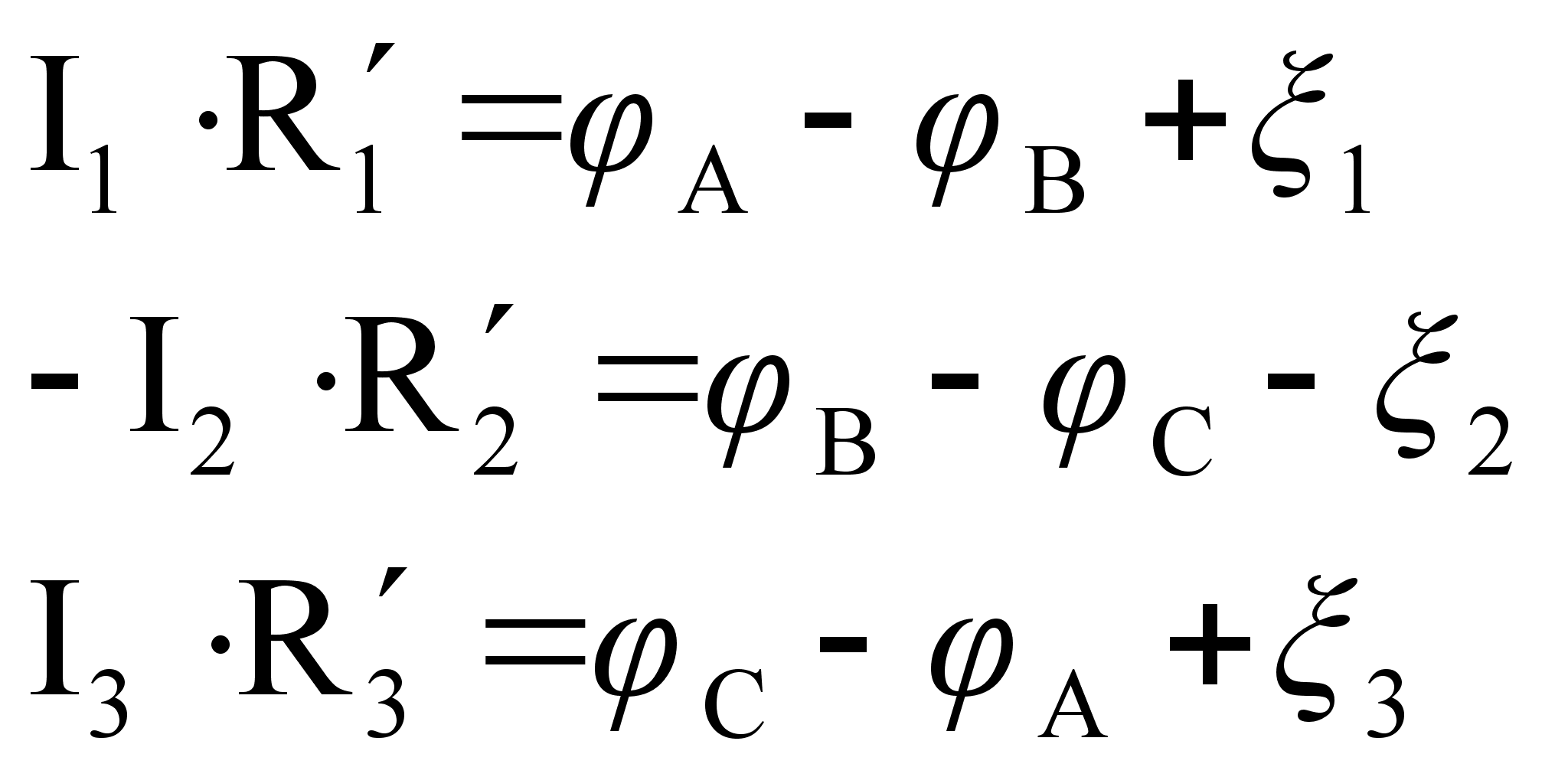
Складывая почленно, получим:
![]()
или
![]() .
.
Сопротивление
источника ЭДС
складывается
с соседним
внешним источником.
Пример: ![]()
Ротор. Теорема Стокса.
Если в движущеёся
жидкости с
распределением
скоростей от
![]() до
до ![]() выделить контур
Г, а остальную
жидкость мгновенно
заморозить,
то в этом контуре
будет продолжаться
движение жидкости.
Мерой такого
действия является
произведение
скорости жидкости
в контуре на
длину контура.
Эту величину
называют циркуляцией
вектора
выделить контур
Г, а остальную
жидкость мгновенно
заморозить,
то в этом контуре
будет продолжаться
движение жидкости.
Мерой такого
действия является
произведение
скорости жидкости
в контуре на
длину контура.
Эту величину
называют циркуляцией
вектора
![]() по контуру Г.
по контуру Г.
Циркуляция
= ![]()
Циркуляция обладает свойством аддитивности, т.е. циркуляция по контуру Г будет равна сумме циркуляций по контурам Г1 и Г2.
Благодаря такому свойству можно ввести понятие удельной циркуляции в точке Р – это векторная величина, называемая ротором или вихрем.
![]()
Рассмотрим циркуляцию по элементарному квадрату в декартовой системе координат.
![]()
Знак минус ставится тогда, когда направления cx не совпадает с направлением обхода.
Учитывая,
что ![]() ,
получим:
,
получим:
![]()
Аналогично для сторон квадрата 2 и 4:
![]() ,
,
Тогда циркуляция по квадрату будет равна:
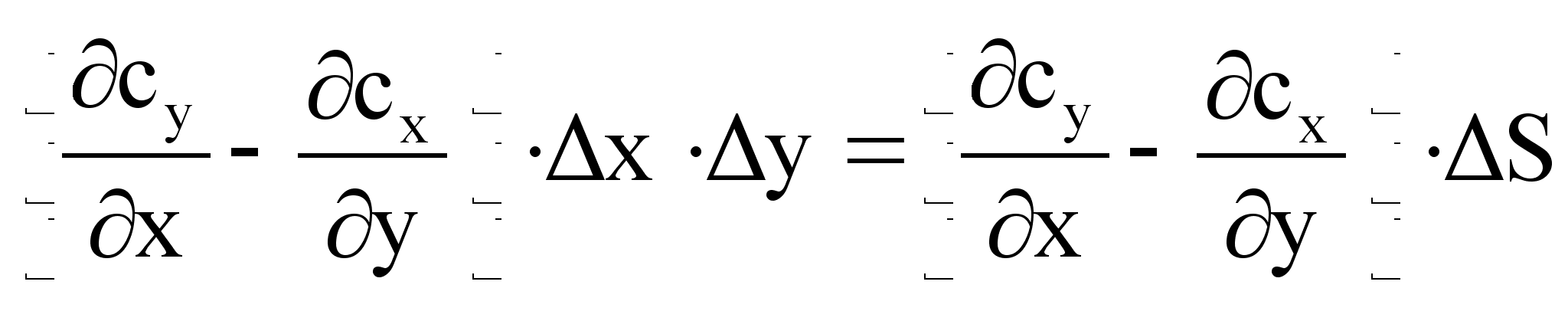 ,
где S –
площадь
квадрата.
,
где S –
площадь
квадрата.
Разделив
циркуляцию
на ![]() ,
найдём проекции
,
найдём проекции
![]() на оси координат:
на оси координат:
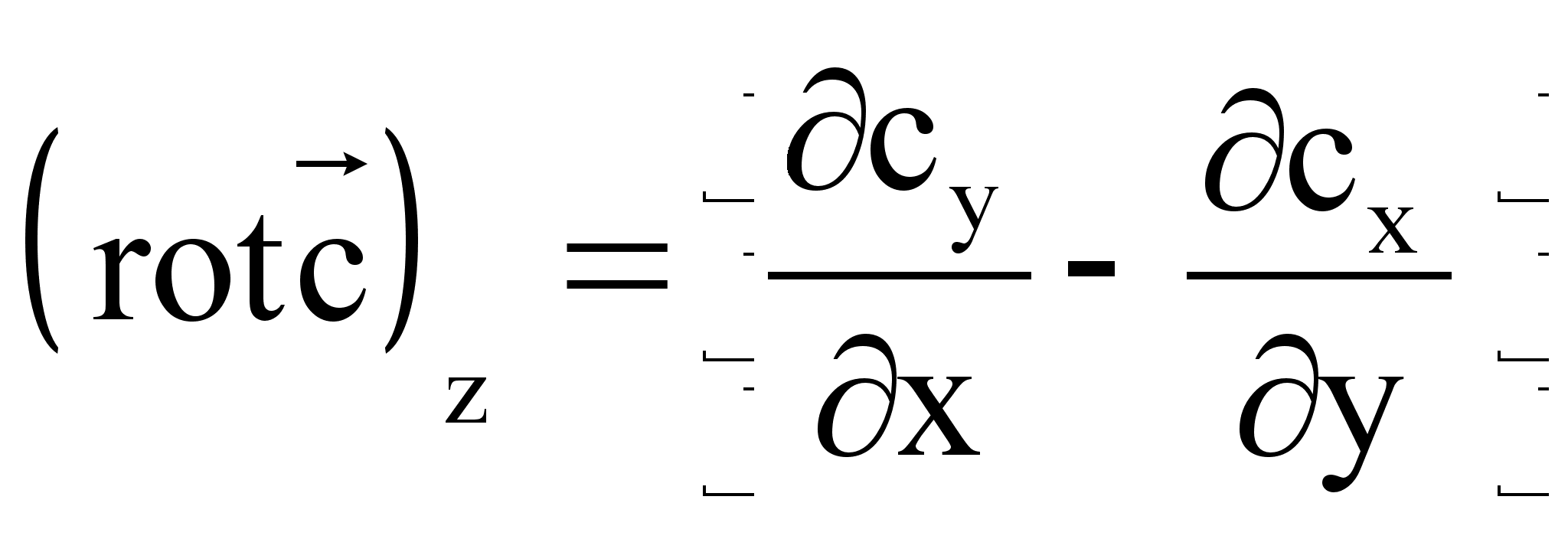 (1*)
(1*)
![]() (2*)
(2*)
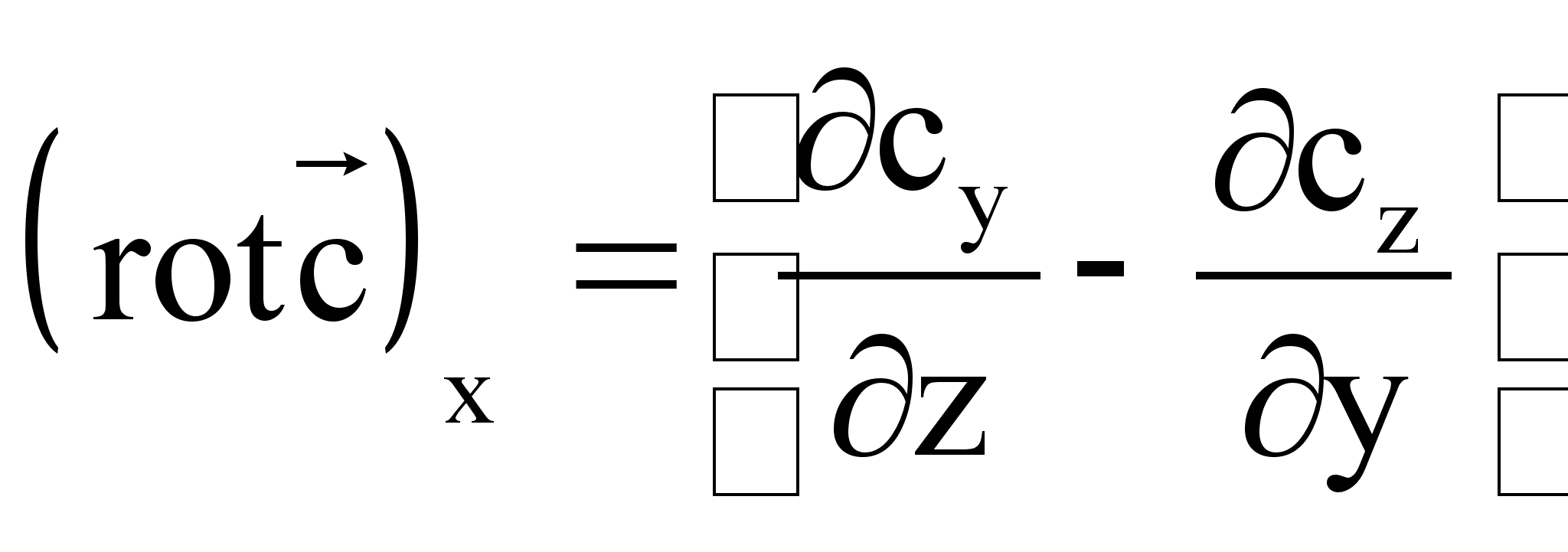 (3*)
(3*)
Любое из выражений (1*) - (3*) можно получить из предыдущего путём циклической системы координат.
Для уравнения
(1*) предыдущим
является уравнение
(3*). Таким образом,
ротор вектора
![]() в декартовой
системе координат
будет иметь
вид:
в декартовой
системе координат
будет иметь
вид:
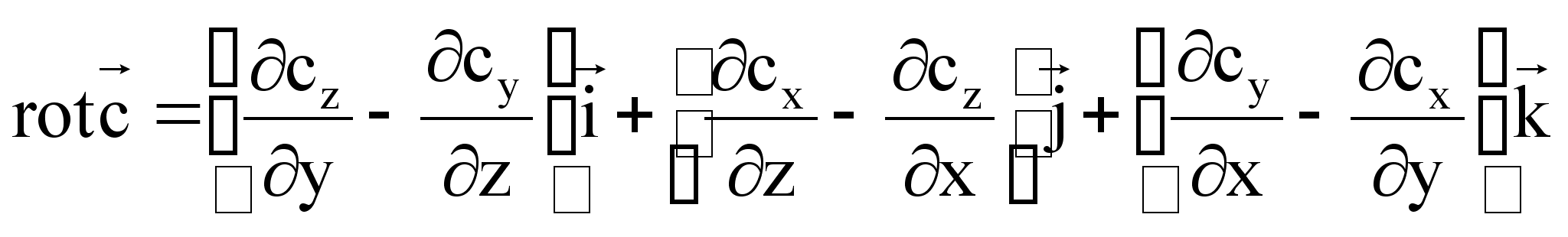
Если известно, что ротор каждой точки поверхности S охватывается контуром Г, то можно вычислить и циркуляцию по этому контуру:
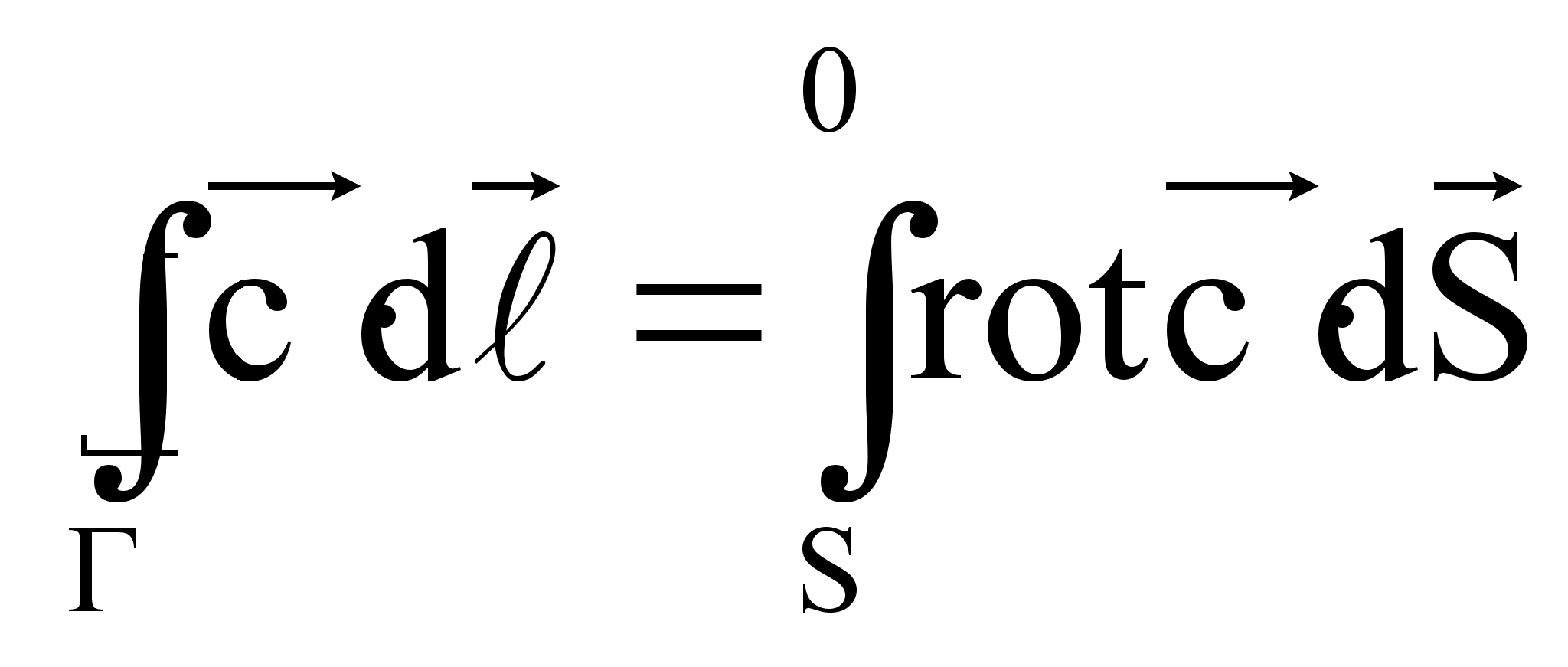
Теорема
Стокса: циркуляция
вектора ![]() по замкнутому
контуру равна
потоку вектора
rot
по замкнутому
контуру равна
потоку вектора
rot![]() через площадку
S,
ограниченную
этим контуром.
через площадку
S,
ограниченную
этим контуром.
Отметим, что
![]()
Мы рассмотрим три вида сочетаний, в которые входит оператор (намбла)

Используя эти сочетания, можно пространственные вариации полей записать в виде независимых от той или иной совокупности осей координат.
Сторонние силы. ЭДС и напряжение.
Для того, чтобы электростатическое поле в проводнике, а вместе с ним и электрический ток не исчезали, необходимо т конца проводника с меньшим потенциалом перемещать заряды, приносимые током, к концу проводника с большим потенциалом. Значит, заряды должны двигаться по замкнутому пути.
(Рисунок)
Известно, что циркуляция электростатического поля (при постоянном токе) равна нулю. Следовательно, в замкнутой цепи должен быть участок, на котором положительные заряды движутся в сторону возрастания потенциала, то есть против сил электростатического поля. Перемещение зарядов на этом участке возможно только с помощью сил не электростатического происхождения, которые называются сторонними силами.
Физическая величина, определяемая работой, совершаемой сторонними силами при перемещении единичного положительного заряда, называется электродвижущей силой (ЭДС).
![]() ,
, ![]() .
(37)
.
(37)
Участок замкнутой цепи представляет собой устройство, в котором происходит разделение разноимённых зарядов и перенос их соответствующим проводникам, называемым источниками тока.
(Рисунок)
Сторонние силы, действующие на заряд q на участке 1-2 можно представить следующим образом:
![]() ,
где
,
где ![]() - напряжённость
поля сторонних
сил.
- напряжённость
поля сторонних
сил.
Работа сторонних сил на участке 1-2 равна:
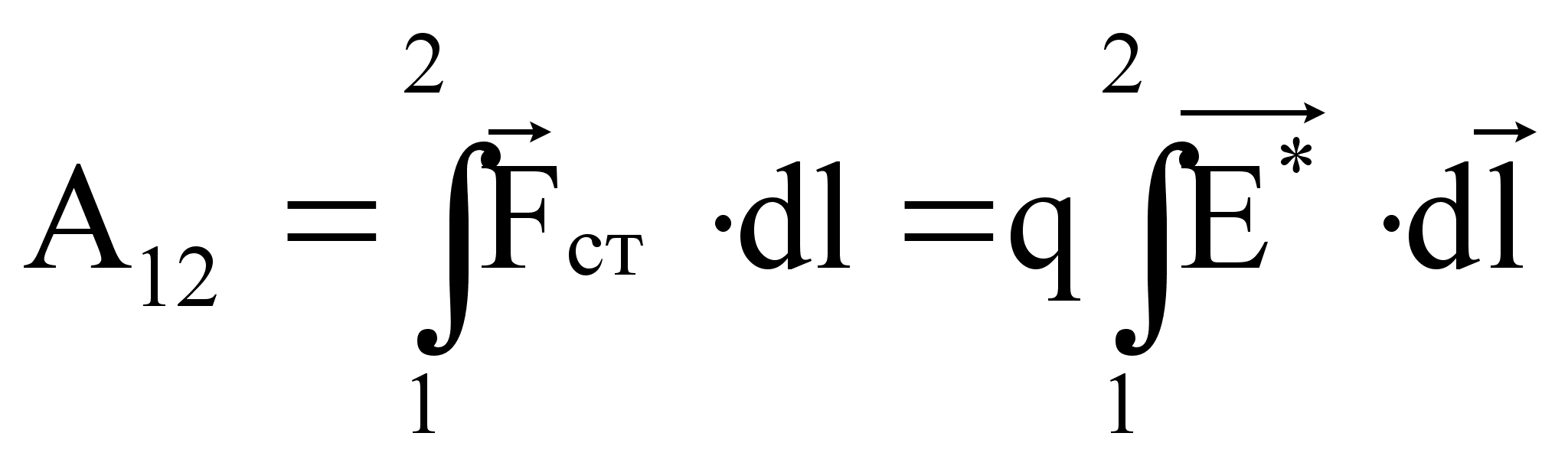
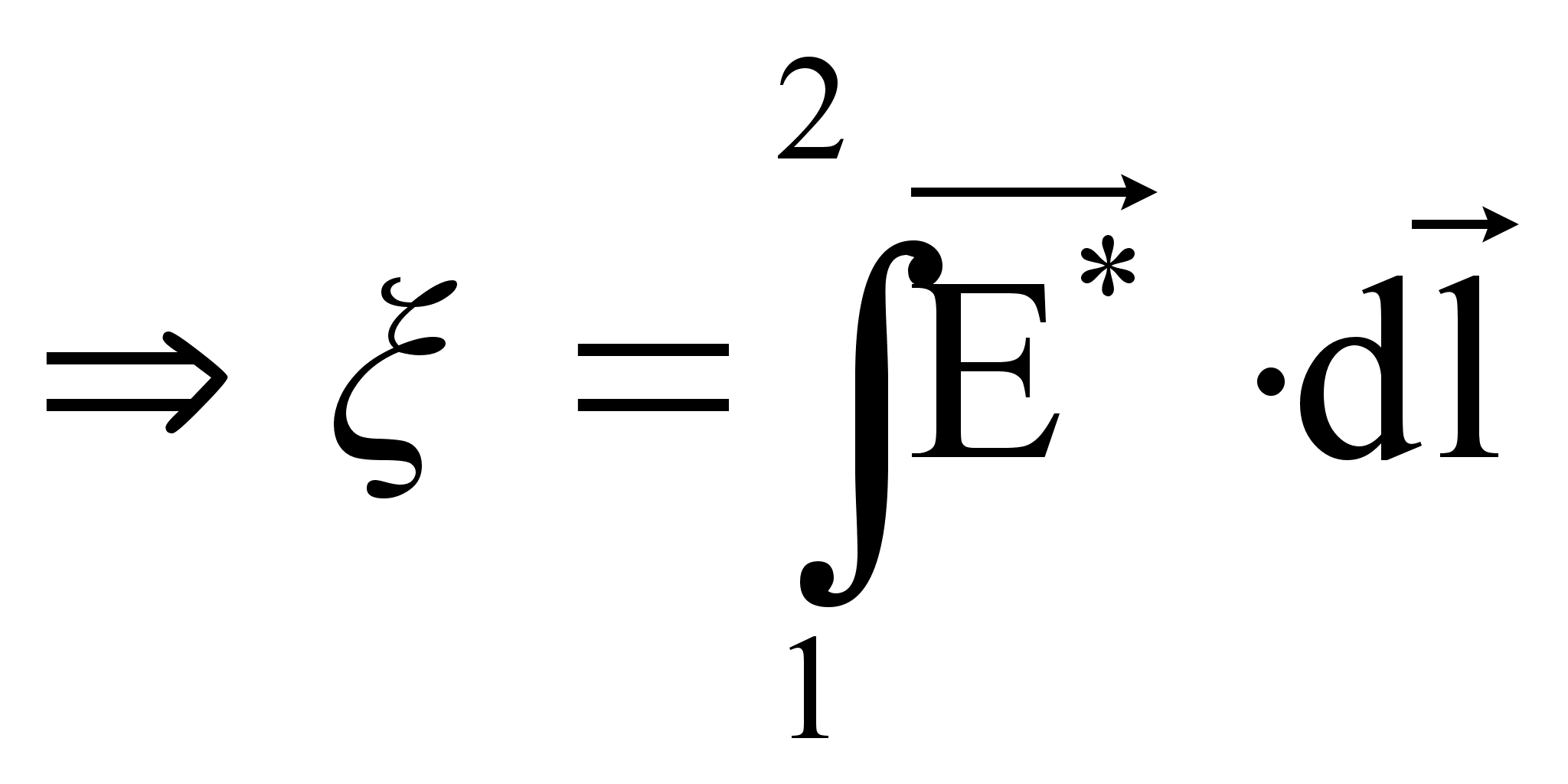 .
.
Для замкнутой цепи:
![]() .
.
Следовательно, ЭДС, действующую в замкнутой цепи, можно представить как циркуляцию вектора напряжённости сторонних сил. На заряд действуют такие силы электростатического поля.
![]() .
.
Тогда ![]() .
.
Работа, совершаемая на участке 1-2 будет равна:
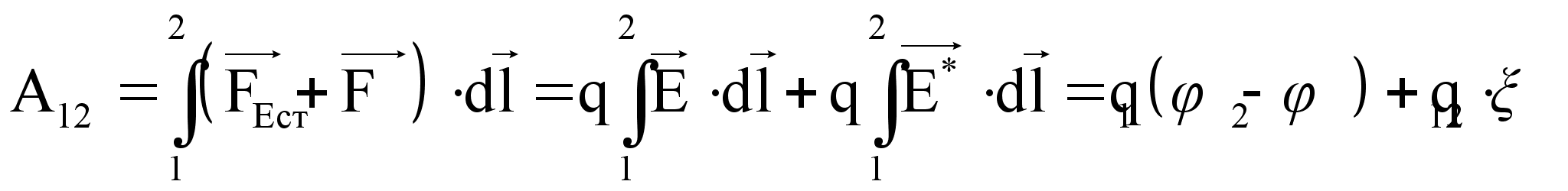
Величина, численно равная работе, совершённой электростатическими и сторонними силами при перемещении единичного положительного заряда, называется падением напряжёния или напряжёнием.
![]()
Участок цепи, на котором действуют сторонние силы, называют неоднородным.
Участок цепи, на котором отсутствуют сторонние силы, называют однородным.
Для однородного участка цепи:
![]() ,
то есть напряжение
совпадает с
разностью
потенциалов.
,
то есть напряжение
совпадает с
разностью
потенциалов.
Электромагнитное поле.
это дискретное явление, при котором минимальный заряд равен заряду электрона.
q e
= ![]() -19
Кл
-19
Кл
q p
= ![]() -19
Кл
-19
Кл
Fкул=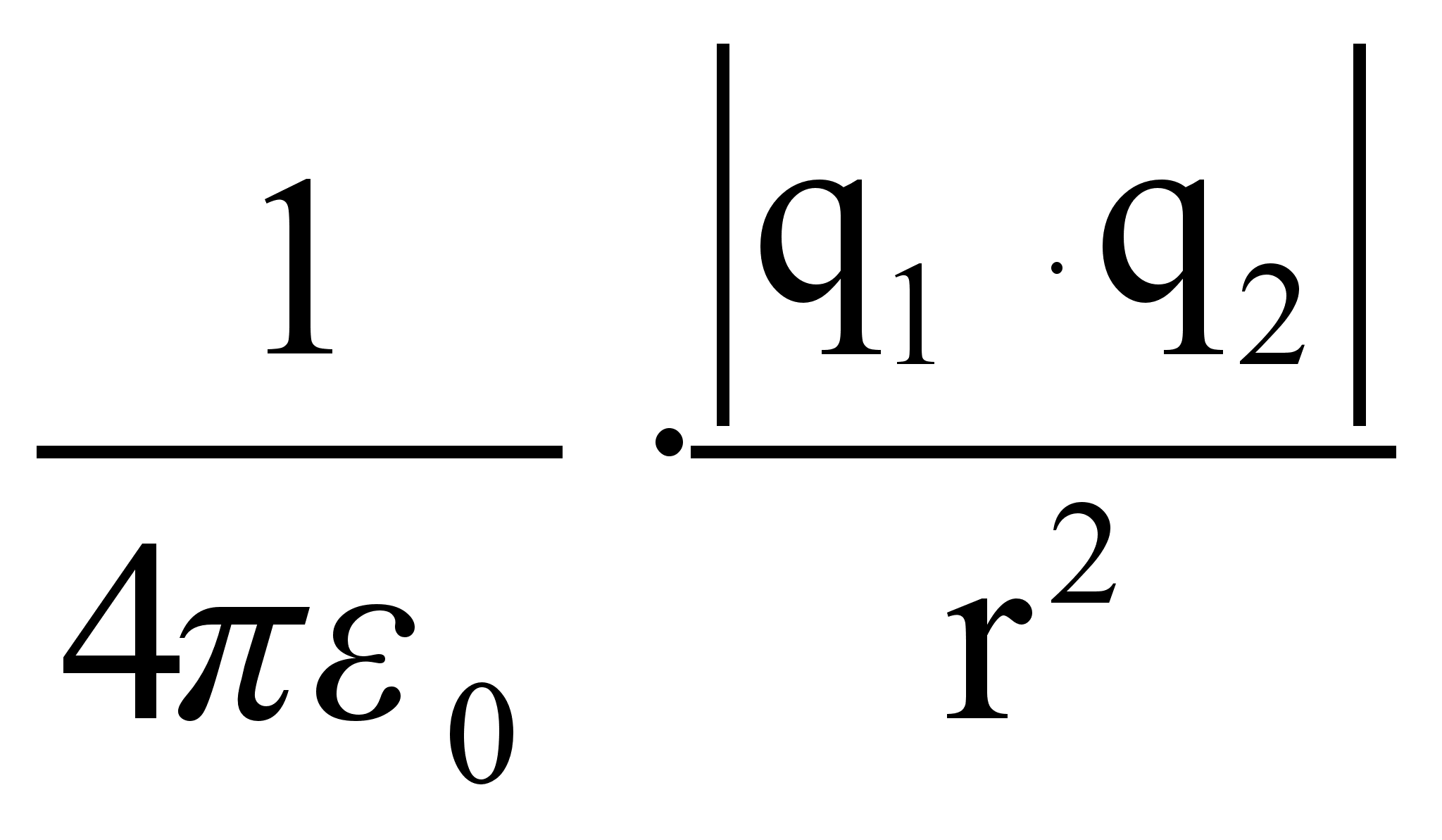 ,
, ![]() =
=
![]() ,
, ![]()
![]()
где q – источник электрического поля
![]() -
пробный заряд
-
пробный заряд
![]() - указывает
направление.
- указывает
направление.
(Рисунок)
Электростатическое поле в вакууме.
(поле неподвижных зарядов)
Напряжённость электростатического поля.
![]()
![]() - напряжённость
поля, созданного
точечным зарядом
- напряжённость
поля, созданного
точечным зарядом
![]()
(Рисунок)
![]()
Для непрерывного распределения заряда суммирование определяется всеми зарядами в произвольной точке пространства:
![]() - по всему
объёму тела
- по всему
объёму тела
(Рисунок)
![]()
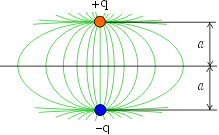
Пример.
(Рисунок)
![]() ,
,
![]() ,
, ![]() -?
-?
точка О – начало отсчёта
![]()
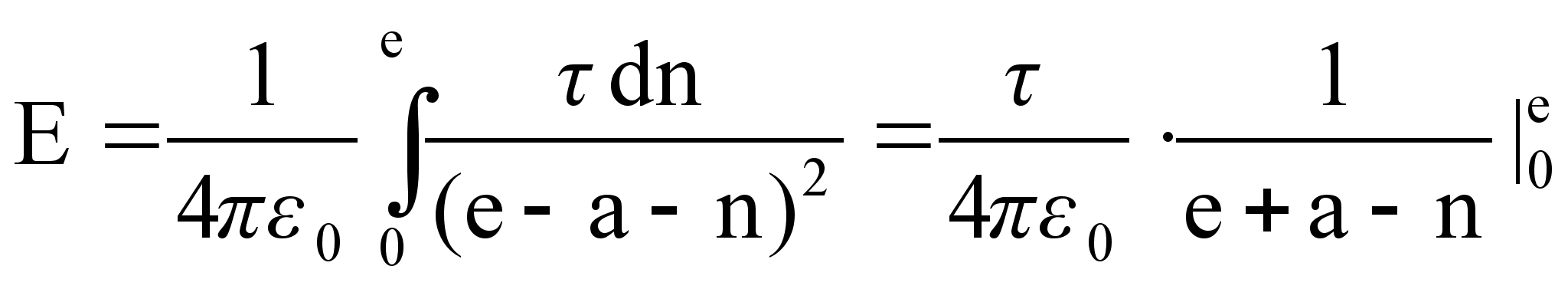
![]()
Похожие работы
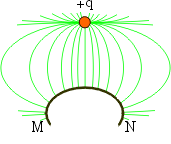
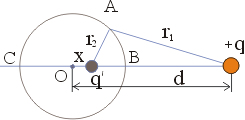
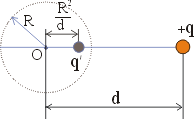
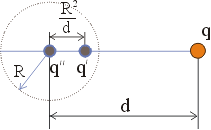
... , не меняя при этом ее потенциал, то поле вне проводника снова останется прежним. Таким образом мы получаем еще одно применение метода изображений - определение полей проводящих поверхностей различной формы. В специальных книгах по электростатике можно найти множество подобных расчетов для различных поверхностей - гиперболоидов, параболоидов и других поверхностей очень хитрой формы. Все подобные ...
... в себя опорный конспект и тетрадь домашних заданий. Предполагается, что если изучать материал, проводя его структурирование и систематизацию, а именно использовать на уроках ОК, а дома тетрадь домашних заданий, то следует ожидать, что качество усвоения учебного материала будет лучше. Для проверки выдвинутого предположения необходимо было разработать методику изучения темы: "Электростатика" 10-го ...
... состоящего из другого вещества. Электризация влияния – возникновение на теле электрического заряда при нахождении его в близи другого заряженного тела (в электрическом поле) Электростатика - раздел электродинамики, изучающий взаимодействие и электрические поля покоящихся электрических зарядов. Электродинамика - классическая, теория электромагнитных процессов в различных средах и в вакууме. ...
... , по-разному записываются в различных системах координат: = (6) (7) (8) = (9) (10) (11) Δ φ = (12) (13) (14) Для цилиндрической и сферической систем выписана лишь радиальная часть соответствующих операторов. Этого достаточно для решения ...

0 комментариев