Навигация
Математическая модель задачи
2. Математическая модель задачи.
f = 186х1 + 125х2 +90х3 ® max
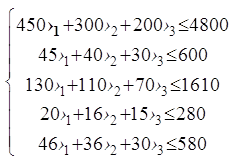
х1 £ 15; х2 £ 9; х3 ³ 9 хj ³ 0, j=1,2,3
3.Экономическое содержание основных и дополнительных переменных.
Основные переменные:
х1 - количество скважин I категории
х2 - количество скважин II категории
х3 - количество скважин III категории
Вводим дополнительные переменные:
х4 - неиспользованные обсадные трубы
х5 - остаток неиспользованных хим/реагентов
х6 - остаток неиспользованных глины и глинопорошка
х7 - остаток талевого каната
х8 - остаток ГСМ
х9 - кол-во скважин I-категории, недостающих до max числа 15;
х10 -кол-во скважин II-категории, недостающих до max числа 9;
х11 –кол-во скважин III-категории, превышающих min число 9;
х12 - количество недостроенных скважин по категориям.
4. Канонический вид.
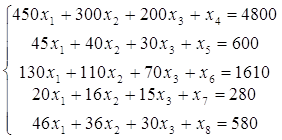
![]()
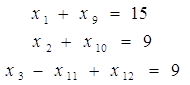
f = 186х1 + 125х2 + 90х3 -М*х12® max
хj³ 0, j=`1;12
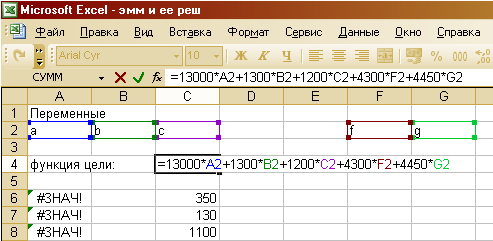
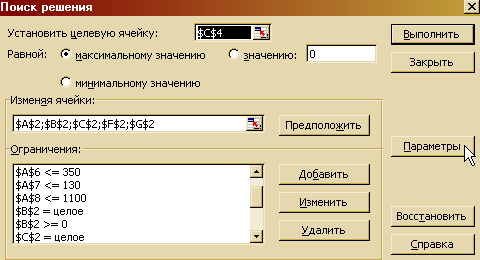
5. Решение симплекс-методом.
| Сб | Хб | план | 186 | 125 | 90 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | |
| Х1 | Х2 | Х3 | Х4 | Х5 | Х6 | Х7 | Х8 | Х9 | Х10 | Х11 | Х12 | ||||
| 0 | Х4 | 4800 | 450 | 300 | 200 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 24 |
| 0 | Х5 | 600 | 45 | 40 | 30 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 20 |
| 0 | Х6 | 1610 | 130 | 110 | 70 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 23 |
| 0 | Х7 | 280 | 20 | 16 | 15 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 18,7 |
| 0 | Х8 | 580 | 46 | 36 | 30 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 19,3 |
| 0 | Х9 | 15 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 0 | Х10 | 9 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| M | Х12 | 9 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | Min 9 |
| Z | 0 | -186 | -125 | -90 | 0 | 0 | |||||||||
| M | -9 | 0 | 0 | -1 | 1 | -1 | |||||||||
| 0 | Х4 | 3000 | 450 | 300 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 200 | 0 | 6,7 |
| 0 | Х5 | 330 | 45 | 40 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 30 | 0 | 7,3 |
| 0 | Х6 | 980 | 130 | 110 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 70 | 0 | 7,5 |
| 0 | Х7 | 145 | 20 | 16 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 15 | 0 | 7,2 |
| 0 | Х8 | 310 | 46 | 36 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 30 | 0 | 6,74 |
| 0 | Х9 | 15 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 15 |
| 0 | Х10 | 9 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 90 | X3 | 9 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | |
| Z | 810 | -186 | -125 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -90 | 90 | ||
| M | 0 | 0 | 0 | 0 | 0 | ||||||||||
| 186 | x1 | 6,67 | 1 | 0,67 | 0 | 0,00 | 0 | 0 | 0 | 0 | 0 | 0 | 0,44 | -0,44 | 15 |
| 0 | Х5 | 30,00 | 0 | 10,00 | 0 | -0 | 1 | 0 | 0 | 0 | 0 | 0 | 10 | -10,00 | 3 |
| 0 | Х6 | 113,33 | 0 | 23,33 | 0 | -0,29 | 0 | 1 | 0 | 0 | 0 | 0 | 12,22 | -12,22 | 9,3 |
| 0 | Х7 | 11,67 | 0 | 2,67 | 0 | -0 | 0 | 0 | 1 | 0 | 0 | 0 | 6,11 | -6,11 | -1,9 |
| 0 | Х8 | 3,33 | 0 | 5,33 | 0 | -0,10 | 0 | 0 | 0 | 1 | 0 | 0 | 9,56 | -9,56 | 0,3 |
| 0 | Х9 | 8,33 | 0 | -0,67 | 0 | -0 | 0 | 0 | 0 | 0 | 1 | 0 | -0,44 | 0,44 | |
| 0 | Х10 | 9 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 90 | X3 | 9 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | -1 | 1 | |
| Z | 2050 | 0 | -1 | 0 | 0,41 | 0 | 0 | 0 | 0 | 0 | 0 | -7,33 | 7,33 | ||
| 186 | X1 | 6,51 | 1 | 0,42 | 0 | 0,035 | 0 | 0 | 0 | -0,047 | 0 | 0 | 0 | 0 | |
| Х5 | 26,51 | 0 | 4,42 | 0 | 0,035 | 1 | 0 | 0 | -1,047 | 0 | 0 | 0 | 0 | ||
| 0 | Х6 | 109,07 | 0 | 16,51 | 0 | -0,79 | 0 | 1 | 0 | -1,279 | 0 | 0 | 0 | 0 | |
| 0 | Х7 | 9,53 | 0 | -0,74 | 0 | 0,10 | 0 | 0 | 1 | -0,64 | 0 | 0 | 0 | 0 | |
| 0 | Х11 | 0,35 | 0 | 0,56 | 0 | -0,92 | 0 | 0 | 0 | 0,10 | 0 | 0 | 1 | -1 | |
| 0 | Х9 | 8,49 | 0 | -0,42 | 0 | -0,03 | 0 | 0 | 0 | 0,05 | 1 | 0 | 0 | 0 | |
| 0 | Х10 | 9 | 1 | 0,00 | 0 | 0,00 | 0 | 0 | 0 | 0,00 | 0 | 1 | 0 | 0 | |
| 90 | X3 | 9,35 | 0 | 0,56 | 1 | 0,00 | 0 | 0 | 0 | 0,10 | 0 | 0 | 0 | 0 | |
| Z | 2052,56 | 0 | 3,09 | 0 | 0,33 | 0 | 0 | 0 | 0,77 | 0 | 0 | 0 | 0 | ||
| M | 0 | 0 | 0 | 0 | 0 |
Оптимальное решение.
Х* = (6,5; 0; 9,35; 0,26,5; 109,1; 9,5; 0,8,5; 9; ), по которому достигается максимальный экономический эффект
Эmax (Х*)=2052,56тыс.руб.
Ответ: Максимальный экономический эффект может достигнуть 2052,56 тыс.руб. если построить скважины так:
I - категории – 6,5
II - категории – 0
III - категории – 9,3
Остатки сырья составят:
1. обсадные трубы -0
2. Химреагенты– 26,51
3. Глина и глинопорошок– 109,1
4. Талевый канат –9,5
5. Гсм - 0
При округлении количества скважин по категориям получаем:
I категория - 6 скважины
II категория - 0 скважины
III категория – 9 скважин
f = 186*6+125*0+90*9 = 1926
Максимальный экономический эффект может достигнуть 1926 тыс.руб. следовательно изменятся остатки:
4800-450*6-300*0-200*9=300 Обсадные трубы - 300
600- 45*6-40*0-30*9= 60 хим/ реагенты - 60
1610-130*6-110*0-70*9=200 глина и глинопорошок - 200
280-20*60-16*0-15*9=25 талевый канат - 25
580-46*6+36*0+30*9=34 ГСМ - 34
2.2 Двойственная задача.Решая двойственную задачу, мы решаем вопрос минимизации общей оценки всего имеющегося количества ресурсов.
6. Математическая модель двойственной задачи.
Пусть уi- стоимость единицы i-го ресурса
Z= 4800у1+600у2+1610у3+280у4+580у5+15у6+9у7-9у8® min
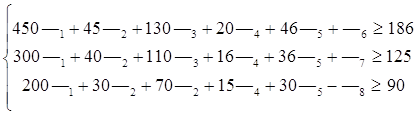
![]()
7. Экономическое содержание двойственной задачи.
При каких значениях уI стоимости единицы каждого из ресурсов в пределах ограниченного объема ресурсов и заданном Экономическом эффекте Эj j-ой скважины общая стоимость затрат Z будет минимальной ?
8. Оптимальное решение двойственной задачи.
Оптимальное решение двойственной задачи найдем из последней строки симплекс-таблицы
Y*=(0,33;0 ,0 ;0 ;0,77 )
Z min(Y*)= 4800*0,33+0+*0+*0+580*0,77=2052,56
Величина двойственной оценки того или оного ресурса показывает, насколько возросло бы максимальное значение целевой функции, если бы объем данного ресурса увеличился на одну единицу.
Вывод: можно построить новый оптимальный план, в котором экономический эффект возрастет на 0,33 тыс.руб , если ввести единицу обсадных труб. А если увеличить расход гсм на единицу, то экономический эффект возрастет на 0,77 тыс.руб.
9. Оценка степени дефицитности ресурсов.
В нашей задаче целью является повышение экономической эффективности плана путем привлечения дополнительных ресурсов, то наш анализ оценок позволит выбрать правильное решение.
Прирост различных ресурсов будет давать неодинаковый эффект, т.е. в избытке у нас такие ресурсы как : глина и глинопорошок, талевый канат и химреагенты. (Остатки даны в пункте 5)
Дефицитными ресурсами в нашей задаче являются обсадные трубы у1= 0,314 и гсм у2= 0,77.
10. Оценить рентабельность производства.
450*0,33+46*0,77=184
200*0,33+30*0,77=89
так как цена не превышает затраты значит предприятие рентабельно.
Литература.
1. Замков О.О., Толстопятенко А.В., Черемных Ю.Н., Математические методы в экономике. Учебник. - М.: МГУ им. М.В. Ломоносова, Изд. «ДИС», 1997г.
2. Коршунов Н.И., Плясунов В.С., Математика в экономике. - М.: Изд. «Вита-Пресс», 1996г.
3. Кузнецов Ю.Н., Кузубов В.И., Волощенко А.Б., Математическое программирование. - М.: Высшая школа, 1976г.
4. Солодовников А.С., Бабайцев В.А., Брайлов А.В., Математика в экономике. Учебник: В 3-х ч. Ч.1. - М.: Финансы и статистика, 1998г.
5. Юдин Д.Б., Гольштейн Е.Г., Задачи и методы линейного программирования. - М.: Сов. Радио, 1964г.
6.Корманов В.Г. Математическое программирование.Учеб.пособие
3-е издание –М: наука 1986 г.
Похожие работы
... : - каждому виду продукции должна соответствовать одна транспортная матрица; - все виды продукции представлены в одной общей матрице с использованием запрещающих тарифов в клетках, связывающих разные виды продукции. 3.2 Решение транспортной задачи на примере ООО «Дубровчанка+» Применяя теорию транспортной задачи к показателям работы ООО «Дубровчанка +», составим следующую транспортную ...
... не может сделать героиней, поскольку Бекки стала (впрочем, и всегда была) одной из жительниц ярмарки тщеславия, где нет достойных называться героями. ГЛАВА II ПОЭТИКА РОМАНА «ЯРМАРКА ТЩЕСЛАВИЯ» 2.1. Функция пролога «Перед занавесом» Предисловие романа озаглавлено «Перед занавесом». Это вводная картина, как бы подготавливающая к тому, о чем будет далее рассказ в произведении. В прологе ...
... для реализации системы бюджетирования Консультационной группы "Воронов и Максимов". Статья о проблемах выбора системы бюджетирования - в проекте "УПРАВЛЕНИЕ 3000". Бюджетный автомат Если вы решитесь на автоматизацию системы бюджетирования компании, перед вами сразу встанут вопросы: что выбрать, сколько платить, как внедрять. Примеряйте! О ЧЕМ РЕЧЬ В “Капитале” на стр. 44, 45 мы рассказали ...
... о правах женщин в свои программы борьбы за равенство. В результате женщины начали создавать свои собственные независимые организации [2, ст. 133-135]. 2. Макросоциологические теории гендера 2.1 Марксистский феминизм В семидесятые годы велись так называемые дискуссии о домашней работе. Марксисты, интересовавшиеся женским вопросом, хотели определить отношение женщин к капиталистической ...
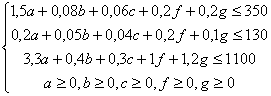
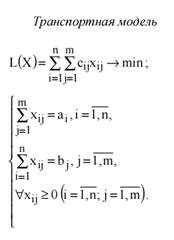
0 комментариев