Навигация
Общие положения по нейронным сетям
4.1. Общие положения по нейронным сетям.
Один из возможных подходов к многомерным и зачастую нелинейным информационным рядам финансового рынка заключается в том, чтобы по возможности подражать образцам поведения участников рынка, используя такие методы искусственного интеллекта, как экспертные системы или нейронные сети.
На моделирование процессов принятия решений этими методами было потрачено много усилий. Оказалось, однако, что экспертные системы в сложных ситуациях хорошо работают лишь тогда, когда системе присуща внутренняя стационарность (т.е. когда на каждый входной вектор имеется единственный не меняющийся со временем ответ). Под такое описание в какой-то степени подходят задачи комплексной классификации или распределения кредитов, но оно представляется совершенно неубедительным для финансовых рынков с их непрерывными структурными изменениями. В случае с финансовыми рынками едва ли можно утверждать, что можно достичь полного или хотя бы в определенной степени адекватного знания о данной предметной области, в то время как для экспертных систем с алгоритмами, основанными на правилах, это — обычное требование.
Н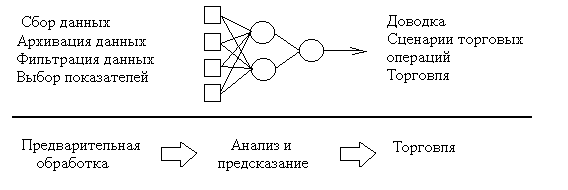
ейронные
сети предлагают
совершенно
новые многообещающие
возможности
для банков и
других финансовых
институтов,
которым по
роду своей
деятельности
приходится
решать задачи
в условиях
небольших
априорных
знаний
о среде.
Рис.2. Блок-схема финансового
прогнозирования при помощи нейронных сетей.
Характер финансовых рынков драматическим образом меняется с тех пор, как вследствие ослабления контроля, приватизации и появления новых финансовых инструментов национальные рынки слились в общемировые, а в большинстве секторов рынка возросла свобода финансовых операций. Очевидно, что сами основы управления риском и доходом не могли не претерпеть изменений, коль скоро возможности диверсификации и стратегии защиты от риска изменились до неузнаваемости.
Возможности такого применения облегчаются тем, что имеются огромные базы экономических данных, — ведь сложные модели всегда прожорливы в отношении информации.
Существенными составными частями нового подхода являются: нейронные сети (сети компьютерных процессоров, взаимодействие которых построено по образцу процессов обучения, происходящих в человеческом мозге). Общей чертой новых методов является возможность распознавания образов и генетические алгоритмы (методы, в которых, исходя из большого набора первоначальных предположений, вырабатывают все более правильные представления о поведении рынка и, в конечном счете, более содержательные рабочие гипотезы). Про методы обоих видов говорят, что они управляются данными, в противоположность подходу, основанному на применении правил, который принят в экспертных системах. Системы, основанные на знаниях, обладают тем недостатком, что построенные на их основе методы торговли оказываются довольно негибкими.
Нейронные сети хорошо приспособлены для решения задач классификации и анализа временных рядов. Задача классификации понимается как задача отнесения предъявленного объекта к одному из нескольких попарно непересекающихся множеств. При этом наиболее важным случаем здесь является бинарная классификация — примерами ее могут служить распознавание доходных и недоходных инвестиций или различение компаний, имеющих хорошие шансы выжить, от тех, которые должны обанкротиться. Способность к моделированию нелинейных процессов, работе с зашумленными данными и адаптивность дают возможность применять нейронные сети для решения широкого класса финансовых задач. Время обучения зависит от сложности задач, от выбора начальных решений и требуемого качества алгоритма.
В связи с этим не представляется возможным рассмотрение модели работа банка , так как полное описание модели требует большого количества переменных и достаточно сложных связей между ними.
Но, тем не менее, есть выход: разбить общую модель на части. Нельзя сказать, что это решит все проблемы .Между тем , такой подход имеет и свои положительные стороны.
Банк аккумулирует временно свободные денежные средства(вклады).Для того, что бы привлечь вкладчиков, необходимо осуществление таких операций и предоставляемых услуг, что бы доход, полученный в результате был бы оптимальным. Одна из предоставляемых услуг : покупка-продажа наличной валюты. Доходы подвержены значительным колебаниям в зависимости от конъюнктуры рынка. В этом случае существенную помощь может оказать, например, прогнозирование курсов валют, ставок.
Рассмотрим прогнозирование ставки доллара к немецкой марке.
4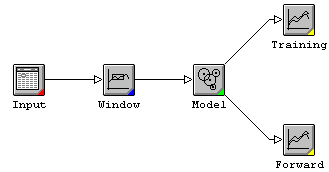
.2.Прогнозирование
ставки доллара
к немецкой
марке.
Рис.3. Общая схема работы.
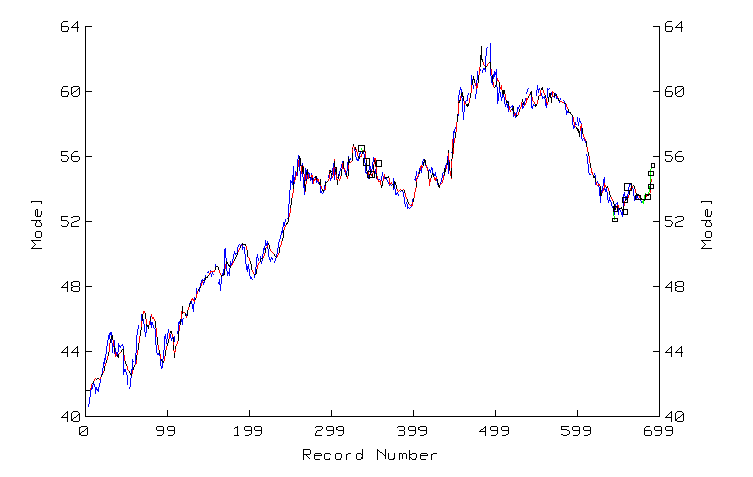
Обучение
происходило
основываясь на информации
о 700 дней. Сеть
использовала
предсказания
изменения
ставки на 1 день
вперед.. Предсказанные
значения для
ставки показываются
черным цветом.
Действительные
значения - серым.
Прямая с квадратиками
– проверочное. (рис.4.)
Рис.4.
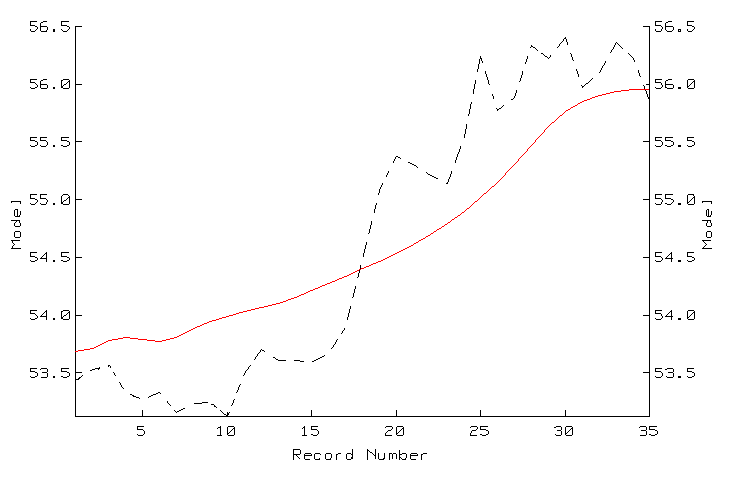
Рис.5.
Во время обучения сети были построены обобщающие правила, основываясь на которых было осуществлено предсказание на 35 дней торговли.(рис.5)
Сеть выводит пунктиром, в действительности - сплошной линией.
Таким образом, благодаря этой информации, банк может подкорректировать работу валютного отдела , избежать ошибок в выборе стратегий , потери денег.
Заключение.
Коммерческий банк - это кредитное учреждение, реализующее экономические интересы. Банковское дело - как правило, весьма выгодный бизнес, основанный на определенных принципах. Основной - прибыльность. Показатель прибыли официально считается основным показателем деятельности банка. Иначе говоря, размер капитала, т.к. в балансовом отчете в разделе собственные средства (капитал) прибыль занимает не последнее место. Размер капитала банка имеет исключительное значение для его деятельности. Во-первых, регулирующие органы устанавливают минимально необходимый размер капитала для вновь создаваемых и работающих банков. Во-вторых, капитал банков служит основой (капитальной базой) для установления регулирующими органами нормативов, определяющих контролируемые показатели их деятельности. Наконец, чем больше размер капитала банка, тем выше уверенность его вкладчиков, кредиторов и клиентов, поскольку при этом повышается его надежность.
Т.о. для получения наибольшей прибыли предполагается создание и организация:
системы информации;
системы прогнозирования денежных ресурсов;
системы принятия решений;
системы контроля.
Представление динамической модели работы банка в виде программы оправды-вает себя, когда число отделов (S) и объемы финансирования (N) достаточно большие. (Уже при S>4 , N>10)
В этом случае преимущества такого подхода к решению задачи неоспоримы, так
как в ручную рассчитать такой объем информации сложно, и программа дает неплохие результаты.
Программа настроена на определенную организационную структуру, базирующуюся на отделах.
Методика, изложенная в данной работе, может быть применена в любом отдельно взятом банке. Например, в следующих банках: Возрождение, Волгопромбанк, Индустриальный, РусЮгБанк, Сава и др.
Приложение 1.
Модель общего вида задачи распределения усилий.
Такой же динамический подход в той же мере справедлив и в случае, когда ограничение нелинейно, и в случае, когда ограничение является линейным..
Модель описывается следующими соотношениями:
Максимизировать 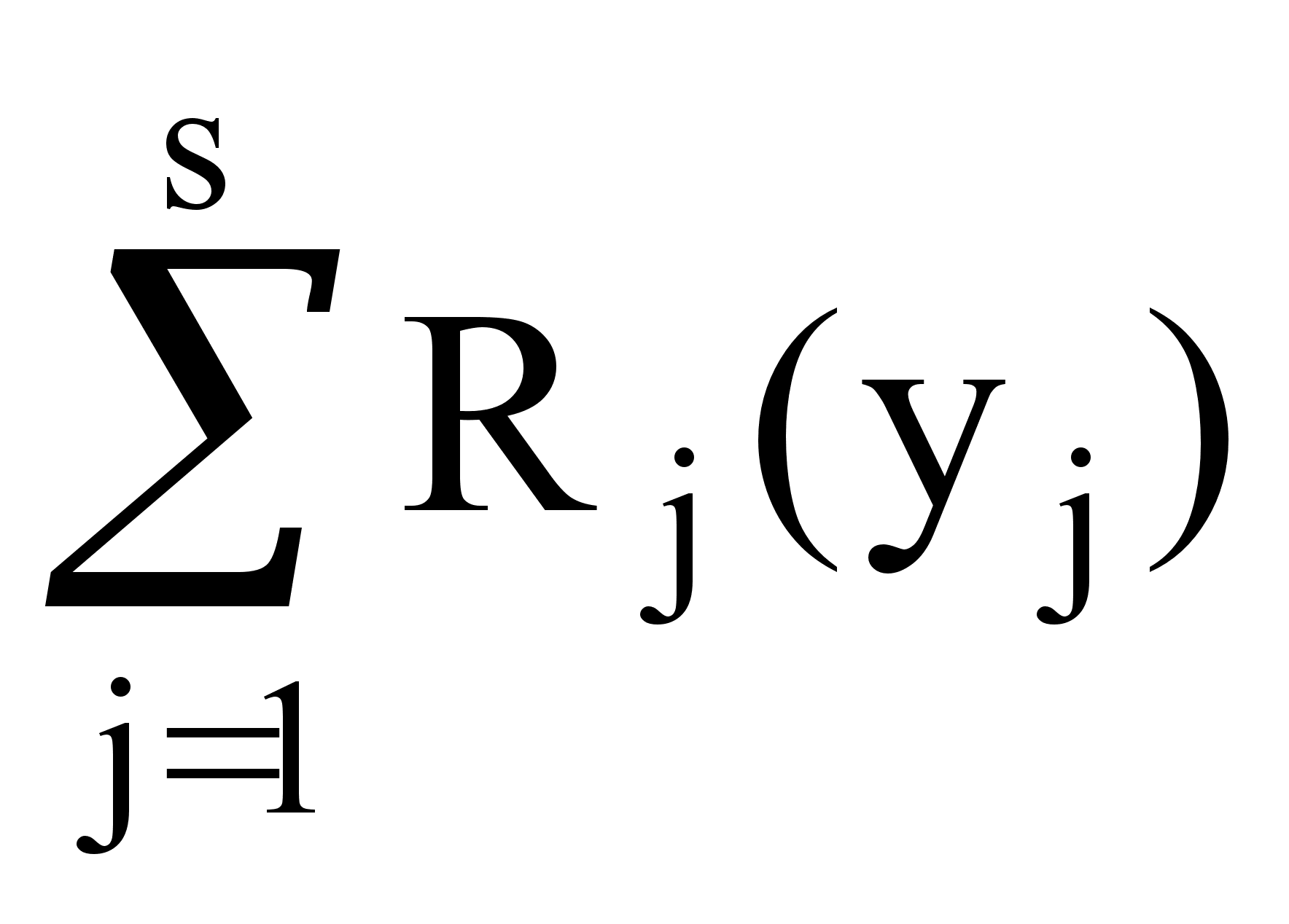 (1’)
(1’)
при ограничениях
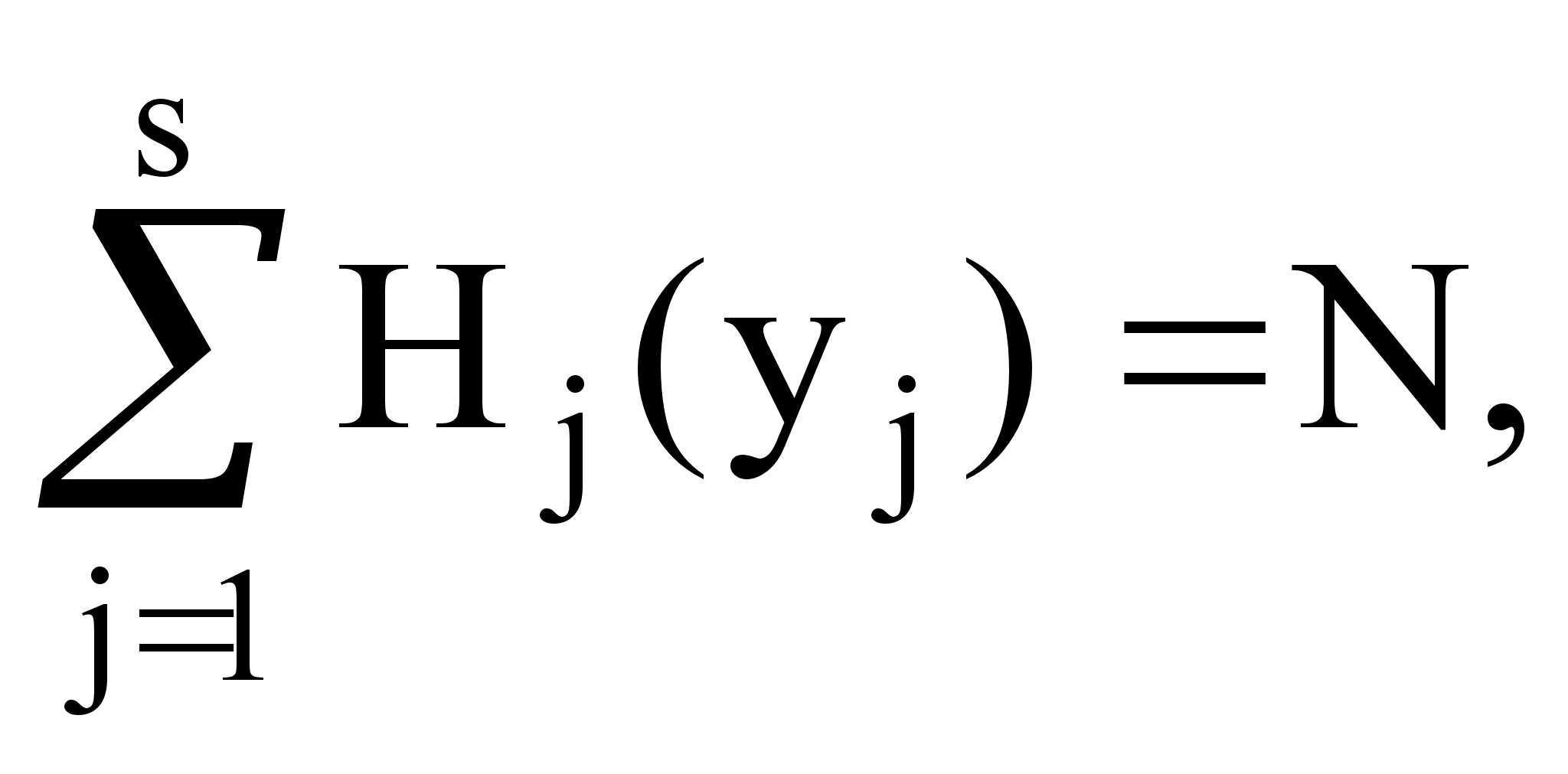 (2’)
(2’)
yj = 0 , 1, 2, ... при любом j. (3’)
Допустим, что каждая функция Hj(yj) есть неубывающая функция, принимающая целочисленные значения при любом yj = 0, 1, 2, ... и удовлетворяющая условию Hj(0) = 0. Для упрощения рассуждений принимается, что H1(y1) = y1, вследствие чего допустимое решение существует при любом значении N. На каждую величину yj можно также наложить ограничение сверху.
Рекуррентное соотношение динамического программирования, соответствующее задаче (1’) — (3’), имеет следующий вид:
gj
= ![]() max
{Rj
(yj)
+gj-1 [
n – Hj(yj)]}, j = 1,2,...,s, (4’)
max
{Rj
(yj)
+gj-1 [
n – Hj(yj)]}, j = 1,2,...,s, (4’)
g0 ( n ) ≡ 0, j = 0 , (5’)
где n = 0, 1, ..., N, а максимум берется только по неотрицательным целочисленным значениям yj, удовлетворяющим условию Hj(yj) ≤ n. Отыскивается значение gs(N). Для выполнения вычислений нужно определить по выражению (4’) значения каждой функции gj(n) при n = 0, 1, ..., N, начиная с j = 1 и заканчивая j=s. [4].
Приложение 2.
Листинг.
{ Динамическая модель работы банка }
program Bank;
uses Crt;
const
S = 10; { Число отделов }
N = 67; { Общий объем финансирования }
Lmax = 17; { Максимальное финансирование отдела }
{ Зависимости доходов от вложений по видам исследований и отделам }
P : array[1..S, 0..Lmax] of integer = (
{0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 }
(0, 0, 3, 1, 1, 22, 10, 17, 2, 9, 10, 6, 6, 17, 14, 10, 10, 10 ),
(0, 0, 3, 1, 1, 2, 10, 17, 9, 2, 11, 7, 6, 13, 13, 13, 13, 13 ),
(0, 0, 3, 8, 1, 20, 17, 6, 6, 6, 6, 7, 7, 8, 8, 8, 8, 8 ),
(0, 1, 3, 1, 1, 22, 10, 17, 3, 9, 20, 6, 6, 17, 14, 10, 10, 10 ),
(0, 1, 30,8, 1, 2, 11, 17, 4, 2, 11,27,26, 33, 33, 33, 33, 33 ),
(0, 1, 3, 7, 1, 14, 17, 6, 6, 6, 6, 7,17, 18, 18, 18, 8, 28 ),
(0, 3, 2, 6, 1, 22, 10, 14, 7, 9, 10, 6, 6, 17, 14, 15, 10, 11 ),
(0, 3, 1, 5, 1, 2, 0, 17, 9, 2, 11, 7, 6, 13, 13, 13, 13, 13 ),
(0, 5, 6, 14,1, 21, 15, 6, 8, 6, 6, 7, 7, 8, 11, 8, 8, 8 ),
(0, 6, 9, 3, 1, 20, 12, 4, 6, 1, 6, 7, 7, 8, 14, 18, 28, 38 )
);
Q : array[1..S, 0..Lmax] of integer = (
{0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 }
(0, 0,13, 3, 3, 23, 30, 15,12,19, 11, 1, 1, 11, 13, 14, 14, 14 ),
(0, 0, 3, 1,11, 2, 10, 17,19, 2, 11, 7, 6, 13, 13, 33, 33, 14 ),
(0, 0, 3, 8,11, 20, 17, 6, 16, 6, 6, 7, 7, 8, 8, 38, 48, 5 ),
(0, 1, 3, 1,11, 22, 10, 17,13, 9, 20, 6, 6, 17, 14, 40, 14, 15 ),
(0, 1, 30,8,11, 2, 11, 17,11, 2, 11,27,26, 33, 33, 32, 34, 35 ),
(0, 1, 3, 7,11, 14, 17, 6, 16,16,16, 17,17, 18, 18, 28, 14, 25 ),
(0, 3, 2, 6,11, 22, 10, 14,17,19, 10, 6,16, 17, 14, 15, 10, 15 ),
(0, 3, 1, 5,11, 2, 0, 17,19,12, 11, 7,16, 13, 13, 13, 15, 13 ),
(0, 5, 6, 14, 11, 21, 15, 6, 18,16,16, 17,17, 8, 11, 18, 18, 18 ),
(0, 6, 9, 3,11, 20, 12, 4, 16,11,16, 7, 7, 8, 14, 18, 28, 38 )
);
R : array[1..S, 0..Lmax] of integer = (
{0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 }
(0, 0, 0, 0, 0, 20, 0, 10, 0, 0, 10, 0, 6, 10, 10, 10, 10, 10 ),
(0, 0,13,11, 1,12, 10, 17,19,12, 11,17,16, 13, 13, 13, 13, 13 ),
(0, 0,13,28,11, 20, 17,16, 16,16,16, 27,37, 38, 38, 18, 18, 8 ),
(0,11,13,21,11, 22, 10, 17, 3, 9, 20, 6, 6, 17, 14, 10, 10, 10 ),
(0,11, 30,8,11,12, 11, 17,14, 2, 11,27,26, 33, 33, 33, 33, 33 ),
(0,11,13,27, 1, 14, 17,16, 16, 6, 6, 7,17, 18, 18, 18, 8, 28 ),
(0,13,12,26, 1, 22, 10, 14,17, 9, 10,26,26, 17, 14, 15, 10, 11 ),
(0,13,11,25,21, 2, 0, 17,19, 2, 11,27,26, 13, 13, 13, 13, 13 ),
(0,15,16,21,21, 21, 15,16, 18, 6, 6, 27,27, 28, 11, 28, 28, 8 ),
(0,16,19,23, 1, 20, 12, 4, 26,21,26, 27,27, 28, 14, 18, 28, 38 )
);
{ Максимальные объемы финансирования отделов }
L : array[1..S] of integer = ( 12, 5, 3, 10, 11, 7, 8, 10, 6, 17 );
function min(a, b : integer) : integer;
begin
if a > b then min := b
else min := a;
end;
var
i, j, y, k, f : integer;
Sum, nn : integer;
pp, qq, rr : array[1..S, 0..Lmax] of integer;
T : array[0..S, 0..N] of record
y, g : integer;
end;
T2 : array[0..3, 0..Lmax] of record
y, g : integer;
end;
Income : array[1..S, 0..3] of integer;
begin
ClrScr;
{ Поиск p(y) }
for j := 1 to S do
for y := 0 to L[j] do
pp[j, y] := P[j, y];
{ Поиск q(y) }
for j := 1 to S do
for y := 0 to L[j] do begin
qq[j, y] := Q[j, 0] + pp[j, y];
for i := 1 to y do
if Q[j, i] + pp[j, y-i] > qq[j, y] then
qq[j, y] := Q[j, i] + pp[j, y-i];
end;
{ Поиск r(y) }
for j := 1 to S do
for y := 0 to L[j] do begin
rr[j, y] := R[j, 0] + qq[j, y];
for i := 1 to y do
if R[j, i] + qq[j, y-i] > rr[j, y] then
rr[j, y] := R[j, i] + qq[j, y-i];
end;
{ Поиск g }
for i := 0 to N do begin
T[0, i].y := 0;
T[0, i].g := 0;
end;
for j := 1 to S do
for i := 0 to N do begin
T[j, i].y := 0;
T[j, i].g := rr[j, 0] + T[j-1, i].g;
for y := 1 to min(L[j], i) do
if rr[j, y] + T[j-1, i-y].g > T[j, i].g then begin
T[j, i].y := y;
T[j, i].g := rr[j, y] + T[j-1, i-y].g;
end;
end;
{ Распределение средств по отделам }
nn := N;
for j := S downto 1 do begin
Income[j, 0] := T[j, nn].y;
nn := nn - Income[j, 0];
end;
{ Распределение средств в каждом отделе }
for k := 1 to S do begin
for i := 0 to Income[k, 0] do begin
T2[0, i].y := 0;
T2[0, i].g := 0;
end;
for j := 1 to 3 do
for i := 0 to Income[k, 0] do begin
T2[j, i].y := 0;
case j of
1 : T2[j, i].g := P[k, 0] + T2[j-1, i].g;
2 : T2[j, i].g := Q[k, 0] + T2[j-1, i].g;
3 : T2[j, i].g := R[k, 0] + T2[j-1, i].g;
end;
for y := 1 to i do begin
case j of
1 : f := P[k, y];
2 : f := Q[k, y];
3 : f := R[k, y];
end;
if f + T2[j-1, i-y].g > T2[j, i].g then begin
T2[j, i].y := y;
T2[j, i].g := f + T2[j-1, i-y].g;
end;
end;
end;
nn := Income[k, 0];
Income[k, 3] := T2[3, nn].y;
nn := nn - Income[k, 3];
Income[k, 2] := T2[2, nn].y;
nn := nn - Income[k, 2];
Income[k, 1] := T2[1, nn].y;
end;
{ Результаты }
WriteLn('Динамическая модель работы банка');
Sum := 0;
for j := 1 to S do begin
for i := 1 to 3 do
WriteLn('y[', j, ', ', i, '] := ', Income[j, i]);
WriteLn('Расход: ', Income[j, 0]);
WriteLn('Доход: ',
P[j, Income[j, 1]] + Q[j, Income[j, 2]] + R[j, Income[j, 3]]);
Sum := Sum + P[j, Income[j, 1]] + Q[j, Income[j, 2]] + R[j, Income[j, 3]];
readkey;
end;
WriteLn('Общий доход: ', Sum);
WriteLn(' Сделанные вложения: ', Sum);
readkey;
end.
Результаты.
y[1,1]=5 y[2,1]=0 y[3,1]=0 y[4,1]=5
y[1,2]=2 y[2,2]=0 y[3,2]=0 y[4,2]=0
y[1,3]=5 y[2,3]=2 y[3,3]=3 y[4,3]=3
Расходы:12 Расходы:2 Расходы:3 Расходы:8
Доходы:55 Доходы:13 Доходы:28 Доходы:43
y[5,1]=2 y[6,1]=0 y[7,1]=5 y[8,1]=0
y[5,2]=2 y[6,2]=4 y[7,2]=0 y[8,2]=0
y[5,3]=2 y[6,3]=3 y[7,3]=3 y[8,3]=5
Расходы:6 Расходы:7 Расходы:8 Расходы: 3
Доходы:12 Доходы:38 Доходы:48 Доходы:25
y[9,1]=3 y[10,1]=5
y[9,2]=1 y[10,2]=5
y[9,3]=1 y[10,3]=3
Расходы:5 Расходы:13
Доходы:34 Доходы:63
Было осуществлено финансирование в размере 67 миллионов долларов.
Общая прибыль составила 437 миллионов долларов.
Итого, чистая прибыль 370 миллионов долларов.
Литература.
1)Банки и банковские операции : Учебник для вузов. / Под редакцией Е.Ф.Жукова.
-М.:Банки и биржи , ЮНИТИ ,1997.
2)Банковское дело / Под редакцией О.И.Лаврушина .-М .: Банковский и биржевой научно- консультационный центр , 1992 .
3)Банковское дело / Под редакцией В.И.Колесникова , Л.П.Кроливецкой .- М.:Финансы и статистика , 1995 .
4)Бэстенс Д.-Э.,Ван Дер Берг В.-М.,Вуд Д. .Нейронные сети и финансовые рынки :принятие решений в торговых операциях. М.:ТВП,Финансы и страховая математика ,т.3.,1997.
5)Вагнер Г. Основы исследования операций.-М.: Мир, т.2 ,1973.
6)Гуриев С.М. ,Поспелов И.Г. .Модель деятельности банка при отсутствии инфляции и экономического роста.// Экономика и математические методы , том 33 , вып.3 ,1997.
7)Киперман Г.Я.,Сурганов Б.С..Популярный экономический словарь .- М.: Экономика , 1993.
8)Перар Ж.Управление международными денежными потоками.- М.:Финансы и статистика,1998.
9)Садвакасов К..Коммерческие банки.Управленческий анализ деятельности .
Планирование и контроль. - М.:Ось-89,1998.
10)Черкасов В.Е.Финансовый анализ в коммерческом банке. – М.:ИНФРА--М, 1995.
11)Юдин Д.Б., Березнева Т.Д.. Статистические и динамические модели стохастического программирования.// Применение исследования операций в экономике.М.:Экономика,1977.
1 Отношение взвешенных, с учетом риска, активов банка к капиталу. Колеблется в пределах от 0.1 до 1.0.
2 Пересчет направления осуществляется на каждом шаге.
3 См. приложение.
4 См. приложение
Содержание: Введение................................................................................................1 Глава1.Банковская система.................................................................2 Глава2.Виды моделей..........................................................................6
2.1.Линейное программирование.............................................6
2.2.Стохастическое программирование...................................7
2.3.Формальная постановка стохастической задачи...............9
2.4.Методы решения.................................................................10 Глава3.Динамическая модель работы банка...................................12
3.1.Вводные сведения...............................................................12
3.2.Постановка задачи..............................................................13 Глава4.Нейронные сети......................................................................16
4.1.Общие положения.............................................................16
4.2.Прогнозирование ставки доллара к немецкой марке.....18 Заключение...........................................................................................20 Приложения..........................................................................................21 Литература...........................................................................................27
Министерство общего и профессионального образования
Российской Федерации
Волжский гуманитарный институт
Волгоградского государственного университета
Кафедра информатики и математического моделирования
дипломная работа
на тему: Моделирование работы банка.
Выполнила: студентка 5 курса
ПМФ - 942 группы
Шалимова М.В.___________
(подпись)
Научный руководитель:
к.т.н., доцент
Мирецкий И.Ю.___________
(подпись)
Заведующий кафедрой:
к.ф.-м.н., доцент
Батхин А.Б.________________
(подпись)
Волжский
19
Похожие работы
... (1.6) Из соотношения (1.6) найдем соответствующее Х, которое будем принимать за случайное число, обозначающее время обслуживания данной кассой. 3. ПРОГРАММНОЕ РЕШЕНИЕ Программа имитационного моделирования работы банка написана на языке C с помощью среды разработки Borland C++ 3.1. Исходный текст программы состоит из следующих файлов: – main.c – содержит реализацию ...
... и очередей к их кассам в каждый момент времени в течение рабочего дня. Критерий оценки результата. Модель должна правдоподобно отражать события реального мира, т.е. работу двух кассиров в банке. Теоретическая часть В общем случае, под имитацией (simulation) понимают процесс проведения на ЭВМ экспериментов с математическими моделями сложных систем реального мира. Целью имитационного ...
... клиента. Промежутки между входами распределены по закону Пуассона с параметром lambda; – void inf (void) - Функция вывода информации пользователю. РУКОВОДСТВО пользователя 1. Программа имитационного моделирования работы банка расположена по следующему адресу: A:Kas1.exe 2. На запрос программы: «Введите количество касс в кассовом зале ж\д вокзала:» Вводим ...
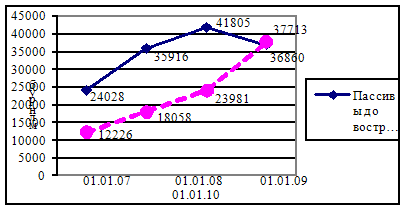
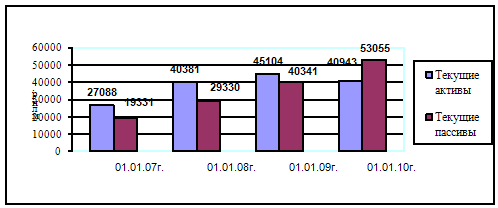
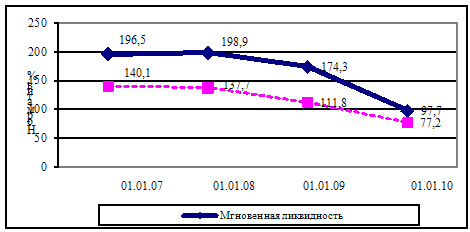
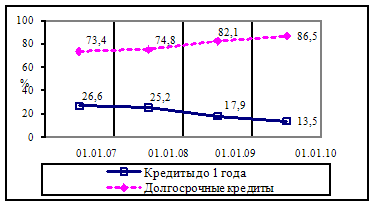
... ликвидности определяется в немаловажной степени и внешними факторами. Их непосредственное воздействие отразилось на внешней стороне ликвидности филиала. Таблица 2.12- Динамика выполнения нормативов ликвидности Филиал №616 ОАО «АСБ Беларусбанк» ОАО «АСБ Беларусбанк» Показатели Нормативное значение На 01.01.2007 На 01.01.2008 На 01.01.2009 На 01.01.2010 На ...









0 комментариев