Навигация
Принцип оптимальності
3.2 Принцип оптимальності
Метою теорії антагоністичних ігор, як і теорії будь-якого класу ігор є відпрацюванння для таких ігор достатньо природних уявлень про оптимальність ситуацій і стратегій гравців та встановлення залежностей між особливостями ігор з одного боку, і особбливостями оптимальних ситуацій у сформульованому змісті ситуацій - з іншого. Найбільш слабкою формою такої залежності можна вважати ознаки існування оптимальних ситуацій, тобто можливості реалізації відповідних понять оптимальності, а найбільш сильною - шляхи ( алгоритми) їх знаходження та обчислення.
Коротко кажучи, оптимальним вважається результат, можливий в умовах тих реалізацій гри, які отримуються внаслідок дій об”єднання, скерованих на досягнення найбільш бажаних ними результатів гри. Дійсний зміст цього виразу може бути дуже різним в залежності від способу оцінуи стратегії об”єднання, тобто від того, як із бажання об”єднання на результатах виводиться її бажання на стратегіях. Крім того, навіть якщо створення кожного з об”єднаннь веде до єдиного результату і відзначеної вище невизначеності немає, то і тоді поняття оптимального результату потребує уточнення, так як через неспівпадання вигідності формування тих чи інших об”єднаннь для різних гравців апріорі незрозуміло, як фактично будуть об”єднуватися самі об”єднання.
Розробка понять оптимальності тісно пов”язана з проблемою можливості їх реалізації, тобто існування оптимальних у відповідному сенсі рішень. З прикладної точки зору бажано, щоб оптимальний результат був достатньо надійним прогнозом результатів розігрування гри, іншими словами, щоб множина оптимальних рішень мала багато “хороших” якостей. Однак часто буває так, що ці хороші якості протирічні, і для скількох-небудь широких класів ігор оптимальних рішень не існує. Тому для гри загального виду від оптимальності доводиться вимагати менше, ніж б хотілося. Розв”язування ігор, що відповідає таким поняттям оптимальності, які в наступному повинні уточнятися, деколи називають передрішеннями.
Рішення є оптимальними, тобто такими, що потенційно реалізуються, якщо жодне об”єднання не зацікавлене втому, щоб виключити його з числа можливих або кожним зацікавленим, що не може цього зробити.
В основу відпрацювання поняття оптимальності для антагоністичних ігор можна накласти наступні міркування.
Якщо другий гравець має в грі Г= тільки одну стратегію yo, тобто y={yo}, то оптимальною стратегією першого гравця та його стратегія, для якої функція Н(*,yo)R досягає на x свого максимуму.
Якщо другий гравець має в грі Г більше однієї стратегії і апріорнаі можливості їх використання першому гравцеві невідомі, або зовсім немає сенсу говорити про ці можливотсі, тоді все вище вказане неможливо застосувати.
Однак на основі сказаного природньо вважати, що оптимальність для першого гравця складається, у всякому разі, у деякій максимізації.
Говорячи формально, це означає, що оптимальною стратегією першого гравця в разі вільної гри Г буде та його стратегія, на якій досягається максимум від деякого функціонала f, визначеного на сімействі всіх функцій виду
Н(*,yo):XR, y єY (3.2)
Принци оптимальності, що базуєтьсяч на максимізації мінімального виграшу, називається принципом максиміну, а вибраниа першим гравцем на його основі стратегія - максимінною стратегією.
Розумною стратегією другого гравця можна вважати ту, при якій найбільші його втрати виявляються мінімальними. Такий принцип оптимальності, що базується на мінімізації максимальних витрат, називається принципом мінімакса, а стратегія для другого гравця, що вибирається у відповідності до цього принципу - мінімаксною стратегією. Відмітимо, що принцип мінімакса, що приймається другим гравцем, є таким з точки зору першого; з власного ж погляду другого гравця , що оцінює свій виграш - Н, його слід називати принципом максиміна.
В загальному принцип оптимальності є таке правило, яке потрібне для рішення конкретної проблеми. Саме цілями дослідження багато в чому визначаються необхідні властивості отриманого результату.
3.3 Змішане розширення матричної гри
По будь-якій матричній грі можна побудувати гру, стратегіями якої є змішані стратегії початкової матричної гри. Змішаними стратегіями гравця називається повний набір можливостей застосування його чистих стратегій.
Пара (X,Y) змішаних стратегій гри Г= називається антагоністична гра Г’=, в якій множинами стратегій гравців є множини їх змішаних стратегій в початковій грі.
Матрична гра, очевидно, є передгрою свого змішаного розширення. Для сідлових точок ігор справедливе звернення до властивості незалежності від сторонніх альтернатив. Крім цього, ця властивість поширюється і на оптимальні стратегії гравців.
Із наявності у матричної гри значення слідує його наявність і в її змішаному розширенні, а також рівність цих двох значень.
3.4 Методи розв”язування матричних ігор
Розглянемо деякі зручні методи розв”язування матричних ігор.
Перший метод розв”язування матричної гри за допомогою лінійного програмування. У цьому методі припускається, що ціна гри додатня. Ця умова не порушує загальності, так як згідно теореми завжди можна підібрвти таке число, додавання якого до всіх елементів матриці виграшів завжди даєє матрицю з додатніх елементів, а, отже, з додатніми значеннями ціни гри. при цьому оптимальні змішані стратегії обох гравців не змінюються.
Так, нехай задана матрична гра з матрицею А=( аij) порядку m*n. Оптимальні змішані стратегії x(x1,...,xi,....,xm), y(y1,....,yi,.....,yn) відповідно першого і другого гравця і ціна гри v повинна задовільняти умовам:
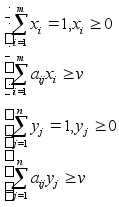 (3.3)
(3.3)
Поділимо всі рівняння і неріності (3.3) на v ( це можна зробити, адже ми припустили що v>0) і введемо наступні позначення:
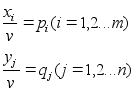
Отримаємо відповідно задачі (3.3) в наступному вигляді

Оскільки перший гравець прагне знайти такі значеня xi, а значить і рі, щоб ціна гри v була максимальна, то розв”язування першої задачі зводиться до знаходження невід”ємних значень рі(і=1,2...m) при яких
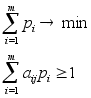 (3.3)
(3.3)
Оскільки другий гравець прагне знайти такі значеня уi, а значить і qі, щоб ціна гри v була максимальна, то розв”язування першої задачі зводиться до знаходження невід”ємних значень qі(і=1,2...m) при яких
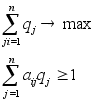 (3.4)
(3.4)
Формули (3.3) та (3.4) виражають двоїстість одна одній задчі лінійного програмування. Для рішення задач існують досить хороші методи, одним з яких є симплекс метод.
Розв”язавши ці задачі, отримаємо значення рі і qі та v. Тоді змішані стратегії, тобто значення xi i yi отримаємо за формулами
xi=vpi (i=1,2...m)
yj=vqj (j=1,2...n) (3.5)
Звичайно це найпростіший метод розв”язання і крім нього є розроблено багато методів, в тому числі і методи, які дозволяєть працювати з матрицями, які не відповідають умовам (3.4).
Похожие работы
... підприємство намагається скоротити шлях товару від заводу до споживача з метою збільшення продажу і зменшення витрат. З цією метою і вибирається один з каналів збуту, які вище розглядалися. 2. Організація збутової діяльності на підприємстві 2.1 Організаційно-економічна характеристика підприємства Відкрите акціонерне товариство “Василівський сирзавод” є колективним підприємством. Відкрите ...
... на ринку). 19) Грошові надходження від фінансово-інвестиційної діяльності З переходом на ринкові основи господарювання зростає значення інвестиційної та фінансової діяльності підприємств. Фінансові інвестиції зумовлені потребою ефективного використання вільних фінансових ресурсів, коли кон'юнктура фінансового ринку уможливлює отримання значно більшого рівня прибутку на вкладений капітал, ...
... РОЗДІЛ 4 ШЛЯХИ ПІДВИЩЕННЯ ЕФЕКТИВНОСТІ ЗЕД ПІДПРИЄМСТВА АТЗТ КОМПАНІЯ "БАСТІОН" 4.1 Заходи щодо удосконалення ЗЕД та їх вплив на ефективність діяльності підприємства АТЗТ компанія "Бастіон" На підставі аналізу діяльності АТЗТ компанія «Бастіон», представленому в розділі 3 дипломної роботи, виявлено, що основними проблемами розвитку ЗЕД підприємства є зниження ефективності його діяльност ...
... ї риби та експортних поставок прісноводної риби. Отримані матеріали дозволяють у дипломному проекті провести детальний аналіз та розробку рекомендацій по оптимізації концепції управління персоналом в ПП „Промен”, яка повинна забезпечити подальший розвиток зовнішньоекономічної діяльності підприємства. СПИСОК ВИКОРИСТАНИХ ДЖЕРЕЛ 1. Митний Кодекс України від 11 липня 2002 року N 92-IV // Із ...
0 комментариев