Информация. Модели. Математическое моделирование

Реферат

Новосибирск 2003г.

Вводные понятия.

Под моделированием понимаются методы получения и исследования моделей. Можно дать несколько определений модели.

Модель – это некоторый объект, который на разных этапах исследования может заменять исследуемый объект.

Модель – это целевой образ объекта оригинала, отражающий наиболее важные свойства для достижения поставленной цели.

Модель – это либо мысленно представляемая, либо материально реализованная система, которая может отображать или воспроизводить объект исследования, а также замещать его с целью изучения и представления новой информации об объекте. Таким образом, создание каждой модели всегда имеет какую-либо цель.

Под целью понимается конечное состояние, при котором изучаемый объект достигает определенного соответствия во времени и пространстве с другим объектом.

Среди основных целей создания модели можно выделить следующие:

Гносеологические (познавательные);

Образовательные;

Управленческие;

Экспериментальные;

Созидательные (проектирование).

Для достижения поставленных целей модель должна обладать некоторыми свойствами, которые одновременно являются и критериями оценки качества построения модели.

Среди свойств модели можно выделить следующие:

Эффективность;

Универсальность;

Устойчивость;

Содержательность;

Адекватность;

Ограниченность;

Полнота;

Динамичность.

Свойство эффективности показывает, насколько правильным было создание и использование модели для достижения поставленной цели. Под универсальностью модели понимается возможность её применения в других задачах и для достижения других целей. Устойчивость модели означает её правильную работу в изменяющихся внешних условиях и экстренных ситуациях. Свойство содержательности определяет количество функции модели.

Среди функций модели выделяют описательную, интерпретаторскую, объяснительную, предсказательную, измерительную функции.

Адекватность определяет соответствие модели поставленной задаче. Модель всегда отображает объект-оригинал не во всех его свойствах и функциях. Таким образом, модель является ограниченной. Под полнотой модели понимается наличие сведений об объекте-оригинале, необходимых для достижения поставленной цели. Динамичность определяет изменение модели с течением времени.

История моделирования определяется серединой 20 века, когда была опубликована монография Норберта Винера «Кибернетика или управление и связь в животном и машине».

Важнейшим в моделировании является понятие информации. Под информацией можно понимать следующее:

Это обозначение содержания полученного из внешнего мира в процессе нашего приспособления к нему. При этом процесс получения и использования информации является процессом нашего приспособления к случайностям нашей среды и нашей жизнедеятельности в этой среде.

Это совокупность, отчужденная от создателя и обобществленная форма знания.

Это модель, то есть упрощенное неадекватное представление знаний.

К примеру, информационной моделью знания можно считать текст, закрепленный на материальном носителе. При этом информационная модель позволяет отделить ценную информацию от несущественной, выбрать аналогии среди различных видов объектов и выбрать в качестве рабочей гипотезы одно из возможных решений.

Классификация моделей.

Единой классификации моделей не существует, но можно выделить следующие типы моделей:

По способу моделирования:

Символические или языковые;

Вещественные или материальные.

По совпадению природы:

Физические совпадения;

Приборные.

По назначению:

Гносеологические, для установления законов природы;

Информационные, для разработки методов управления;

По способу построения моделей:

Теоретические (аналитические) – по данным о внутренней структуре;

Формальные – по зависимости между входом и выходом в систему;

Комбинированные.

По типу языка описания:

Текстовые или дескриптивные;

Графические (чертежи, схемы);

Математические;

Смешанные.

По зависимости параметров модели от пространственных координат:

С распределенными переменными (изменяются в пространстве);

С сосредоточенными переменными (не изменяются в пространстве).

По зависимости от переменных:

Независимые;

Зависимые.

По принципу построения:

Стохастические или вероятностные;

Детерминированные (причинно обусловленные).

По изменению выходных переменных во времени:

Статические или стационарные;

Динамические или нестационарные.

По приспособляемости модели:

Адаптивные;

Неадаптивные

По способу приспособления, настройки (для адаптивных моделей):

Поисковые (по минимуму ошибки);

Беспоисковые.

По степени соответствия оригиналу:

Изоморфные (строго соответствующие объекту);

Гомоморфные (отражает некоторые существенные свойства объекта).

По природе:

Материальные или геометрического подобия (фотография);

Знаковые, в том числе графические и математические;

Дескриптивная.

По принципу моделирования:

Физические модели, в том числе геометрические (модель самолета);

Аналоговые модели имеют либо сходную структуру со структурой объекта (структурная модель) или выполняют подобные объекту функции (функциональная модель). Принцип аналогии является основным принципом моделирования. Примером аналогии является исследование экономических систем с помощью исследования «потока» электричества в цепи.

Символические модели – это абстрактные математические уравнения (неравенства).

С помощью данной классификации можно определить модель с разных точек зрения.

В результате современных исследований можно создать управленческую (кибернетическую) модель, в которой отражаются аспекты структурной, функциональной, информационной и математической модели.

При этом любую систему можно изучать на двух уровнях:

Теоретическом, или фундаментальными методами;

Эмпирическом, или прикладными методами.

Фундаментальные методы объясняют и предсказывают будущие открытия, а прикладные методы позволяют решать отдельные, не глобальные проблемы.

На эмпирическом уровне система изучается через связи с внешней средой, через свойства и отношения между объектами системами. На первом этапе изучения системы создается дескриптивная модель, которая не содержит управляющих факторов. На втором этапе создается конструктивная модель, которая позволяет выявить существующие факторы с целью эффективного управления ими.

Классификация объектов (систем) по их способности использовать информацию.

Система представляет собой ограниченное и взаимосвязанное единство различных объектов живой и неживой природы.

Пользуясь данной классификацией можно выделить 7 типов систем:

Простое преобразование.

где, I – входная информация;

O – выходная информация.

Собственная цель отсутствует. Непрерывные указания идут от внешнего источника, и при этом реализуются 3 операции:

прием;

переработка, или преобразование;

выходное воздействие.

Пример: процесс превращения заказа в товары, звуковые усилители.

Простая сортировка.

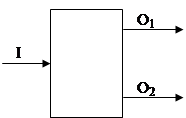
Система имеет два выхода и один вход. Правила сортировки реализованы в блоке преобразования. Это простые операции поиска и распознавания.

Обратная связь.

А – блок получения ошибки.

С – блок формирование сигнала обратной связи.

В – исполнительный механизм.

Дуга СА – обратная связь.

Дуга АВ – ошибка.

Часть выходного сигнала сравнивается с установленным на входе сигналом, и анализируются рассогласования. Обычно обратная связь уменьшает ошибку и называется отрицательной обратной связью, так как направлена противоположно действию. Примером является система планирования, где анализируется устойчивость, время запаздывания и осуществляется контроль. Также примером является движение антенны радара.

Сортировка с обратной связью.

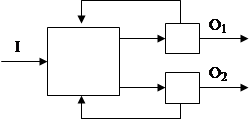
Система с автоматическим изменением цели, или обратная связь второго порядка.

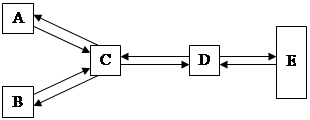
В этой системе реализуется выбор при изменении внешних условий.

А – рецептор.

B – эффектор.

С – принятие решений.

D – выборка из памяти.

E – память.

По такой схеме реализуется процесс обучения любой организации.

Система с сознательным изменением цели, или обратная связь третьего порядка.

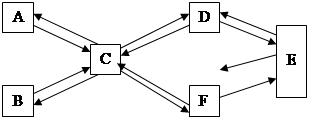
F – переработка информации.

Сознание – это представление об объекте, о цели, об управлении рецептором и эффектором; о процессах, связанных с памятью.

Память – это коллективное знание, где реализуются хранение, поиск, обработка данных.

В этих системах из большого объема внешней информации выбирается такая, которая необходима субъекту (человеку, организации). Такая система может управлять собственным ростом и развитием.

Комбинированные.

4 Этапы создания модели.

1 – система (объект, явление, процесс).

2 – описание системы.

3 – постановка задачи.

4 – математическая модель.

5 – непротиворечивость выводов в рамках модели.

6 – решение задачи.

7 – проверка адекватности

8 – уточнение модели.

При изучении любого объекта путем моделирования нужно выполнять ряд обязательных, вышеперечисленных этапов.

Дуга (1 – 2) – наблюдение эксперимента.

Дуга (2 – 3) – формализация абстракции, то есть описание существенных факторов и связей между ними.

Дуга (3 – 4) – конструирование элементов модели.

Дуга (4 – 5) – изучение модели.

Дуга (5 – 6) – выбор методов решения.

Дуга (6 – 7) – сравнение выводов с реальными фактами.

Решение, полученное на модели, действительно только до тех пор, пока неуправляемые параметры сохраняют свои значения, и соотношения между параметрами модели остаются постоянными. Если решение выходит из-под контроля, то теряется возможность управления им, тогда устанавливается процедура подстройки решения.

Так как модель всегда лишь частично отображает действительность, то она может быть хорошей, если будет точно предсказывать влияние изменений в системе на общую эффективность всей системы. Решение можно оценить, сопоставив результаты, полученные по модели, с ранее полученными данными, или с данными практических испытаний.

Многокритериальные задачи обычно решаются как последовательность однокритериальных задач. Критерий оптимизации, в данном случае, называется целевой функцией. Затем формируются ограничения, и выбирается один из следующих методов решения:

Дедуктивный, или аналитический.

Индуктивный, или численный.

Метод Монте-Карло, или статистических испытаний.