Навигация
Взаимодействие двух группировок
3. Взаимодействие двух группировок.
Рассмотрим достаточно типичную ситуацию борьбы идей двух взаимодействующих группировок. Типичным примером является, например, борьба приверженцев модернизированных и традиционных ценностей.
Пусть величина х обозначает количество приверженцев новой ценности, а величина у – количество ее противников. Будем считать, что рост величины х обусловлен естественными причинами, а ее уменьшение – сопротивлением противников. Тогда коэффициент роста для величины х можно представить в виде:
ax=mx–nxy (3.1)
Отражено то, что сопротивление росту х возрастает с увеличением количества противников у.
Наоборот, для второй группировки характерно естественное убывание при отсутствии врагов и рост при возрастании количества врагов. Поэтому коэффициент роста для величины у представим в виде:
ay=myx–ny (3.2)
Система дифференциальных уравнений, отражающая совместную эволюцию двух группировок, в итоге принимает вид:
![]() (3.3)
(3.3)
![]()
В экологии подобные уравнения были впервые предложены итальянским ученым Вольтеррá для описания взаимодействия популяций хищников и жертв. В данном случае условно роль жертв играют приверженцы новой ценности, а роль хищников – ее противники. В зависимости от идеологической позиции наименования могут быть противоположными. Эта модель отражает многозначность вариантов и может иметь эвристический характер.
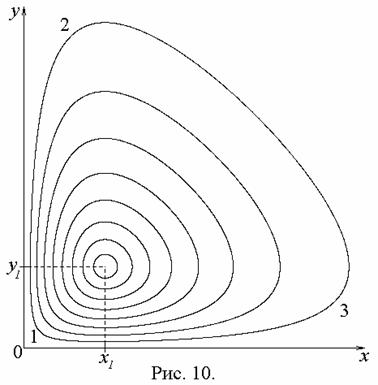
Решение уравнений (3.3) удобнее всего производить численным методом с применением компьютера. На рис. 10 приведены некоторые характерные графики. Видно, что имеется равновесное состояние со значениями:
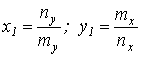 (3.4)
(3.4)
При малых отклонениях от равновесного состояния происходят небольшие колебания с малыми амплитудами изменения обеих величин х и у.
Рассмотрим подробно случай больших отклонений от равновесного состояния. Пусть в некоторый начальный момент времени малы обе величины х и у (точка 1 на рис. 10). Это может соответствовать состоянию, когда новая ценность только что возникла, мало число ее сторонников, но мало и противников, поскольку бороться пока не с чем.
При отсутствии заметного сопротивления идея, ценность начинает быстро приобретать своих сторонников; на рис. 10 это показано в виде быстрого роста у при почти неизменном х (участок 1–2).
Но при значительном увеличении количества сторонников новой ценности, активизируются ее враги и начинается быстрый рост их количества у. Рост у сопровождается уменьшением х, т.е. количество противников ценности растет несмотря на то, что количество ее сторонников быстро уменьшается (участок 2–3).
В конце концов, складывается состояние (точка 3 на рис. 10), когда сторонников новой ценности почти не остается, но зато имеется очень много ее противников. Поскольку бороться уже не с кем, противники быстро исчезают (в том смысле, что начинают заниматься какими-то другими делами). Происходит переход из 3 в 1, т.е. в исходное состояние.
Такие циклические процессы наиболее хорошо изучены в экологии; несомненно, они имеют место и в обществе.
Возможны и многие другие модели взаимодействия двух группировок между собой. К примеру, пользуясь аналогией с экономическими моделями, приведем еще два характерных графика. На первом из них (рис. 11) приведен пример совместной эволюции двух систем при наличии взаимной конфронтации.
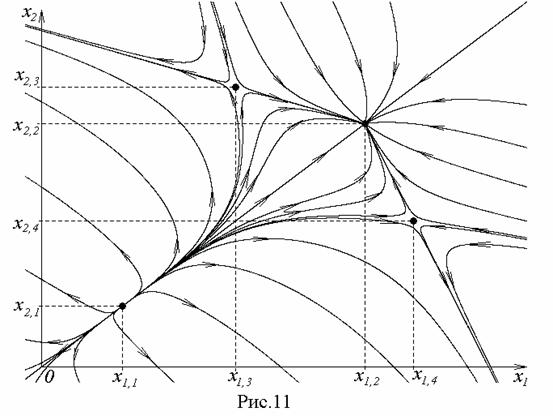
Система имеет несколько положений равновесия, но большинство из них неустойчивы и поэтому отклонения от таких положений приводят к разрушению системы (что выражается в отрицательных значениях) величин х1 и х2. Главной причиной неустойчивости является то, что каждая из группировок озабочена, в первую очередь, не собственным обустройством, а нанесением ущерба другой группировке.
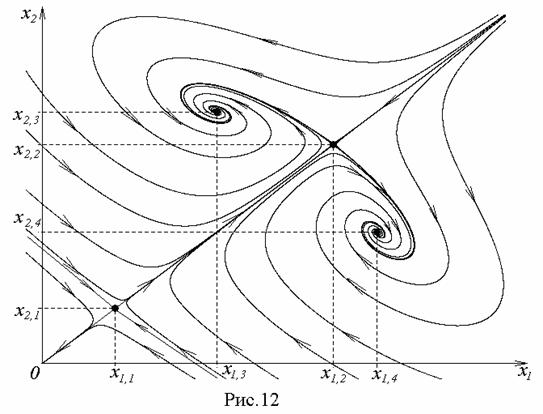
На рис. 12 приведен график взаимодействия двух группировок при отсутствии конфронтации. Те же цели, что и в предыдущем случае, достигаются теперь не за счет вражды с соседней группировкой, а за счет преимущественно самостоятельного решения своих проблем. При этом система имеет два устойчивых состояния равновесия; выход на одно из них гарантируется практически при любых исходных условиях.
Выводы.
Рассмотренные применения математических моделей к изучению процессов модернизации позволяют сделать выводы о перспективности математических методов в социологии.
Методы, основанные на использовании дифференциальных уравнений, обладают двумя очевидными достоинствами. Во-первых, в тех случаях, когда возможна идентификация параметров уравнений, они позволяют делать какие-то прогнозы или рекомендовать методы управления ситуациями.
Во-вторых, даже в тех случаях, когда получение количественных результатов по каким-то причинам затруднительно (например, из-за трудности получения соответствующего экспериментального материала), использование дифференциальных уравнений позволяет делать качественный анализ различных ситуаций, что в ряде случаев может иметь ценность не меньшую, чем конкретные количественные результаты.
Постановка задач применения известных в экологи, генетике, экономике для исследования социальных процессов с соответствующими содержательными интерпретациями обогатит социологическую науку.
Список литературыАрнольд В.И. Теория катастроф. М., «Наука», 1990. – 128 с.
Моисеев Н.Н. Математические задачи системного анализа, М., «Наука», 1981. – 487 с.
Пономаренко О.І., Пономаренко В.О. Системні методи в економиці, менеджменті та бізнесі. – К., «Либідь», 1995. – 239 с.
Похожие работы
... , выявить в ней место религии как социального института и рассмотреть систему связей религии и других социальных институтов. Это позволит дать ответ на поставленную задачу, как религия влияет на социокультурные трансформации. Следует еще раз отметить, что сама постановка вопроса о влиянии религии на социальную систему, как уже отмечалось, является реакцией на материалистическое понимание истории, ...
... это язык для выражения подспудного знания общего для многих и многих. Сделаем допущение об автобиографичности рок-песни. Искренность, исповедальность - это то, что делает рок-песню захватываю щей и близкой. Разбирая смысл песен, препарируя их содержание мы неожиданно находим много неприятных слов о герое песен. Здесь приоткрывается еще одна тайна привлекательности песен. Герой их не похож на ...
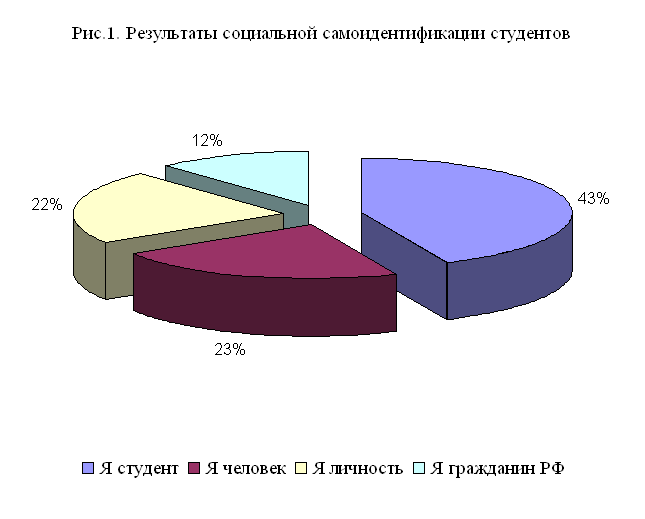
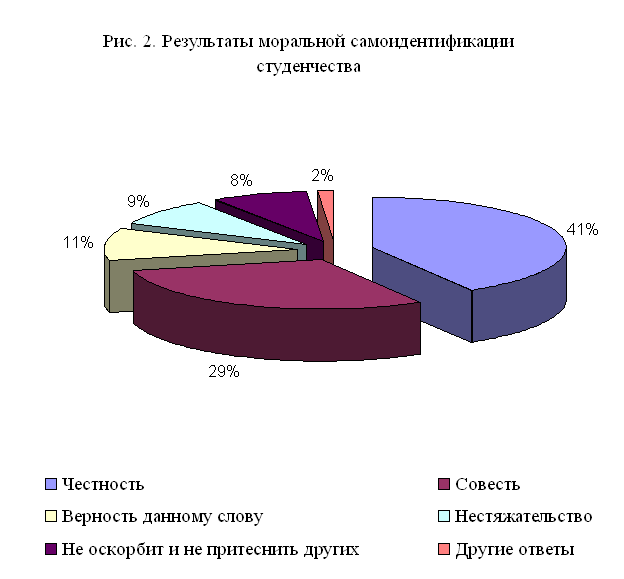
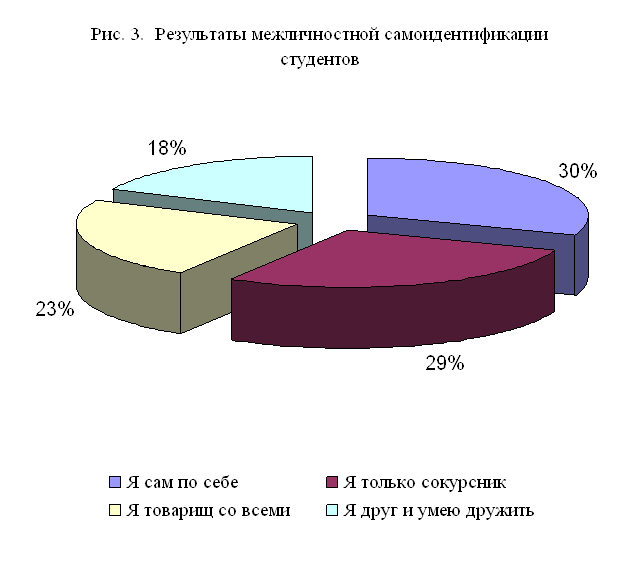
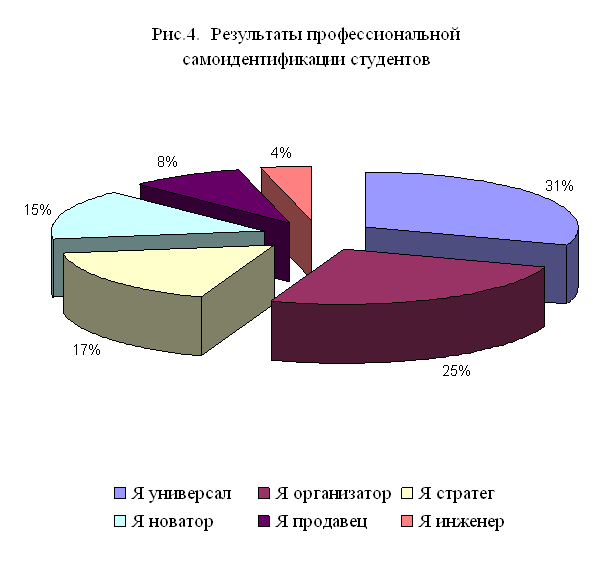
... в своих взглядах и идеях потенцию будущих политических, культурных и экономических преобразований в обществе. ГЛАВА II. РЕГИОНАЛЬНЫЕ ОСОБЕННОСТИ САМОИДЕНТИФИКАЦИИ СОВРЕМЕННОГО СТУДЕНЧЕСТВА 2.1. Основные направления социокультурной самоидентификации студенчества в регионе Для определения основных направлений социокультурной самоидентификации студенчества в Ставропольском ...
... общества, возникает «интерактивное» одиночество, спецификой которого является вытеснение живых социальных контактов контактами виртуальными. Выводы и рекомендации Анализ информационных технологий как средства трансформации повседневной жизни человека, проведённый в данной работе, позволил сделать следующие выводы. 1. Повседневность – это сфера эмпирической жизни человека, характерными ...
0 комментариев