Броун, Роберт (Brown, Robert) (1773–1858), английский ботаник. Родился 21 декабря 1773 в Монтрозе.
Изучал медицину в Абердинском и Эдинбургском университетах (1789–1795). В течение пяти лет работал ассистентом хирурга в Британской армии. В 1798 во время пребывания в Лондоне познакомился с Дж.Бэнксом, президентом Королевского общества, и в 1801 по его рекомендации был приглашен принять участие в экспедиции, направлявшейся в Австралию. В 1805 возвратился в Англию с коллекцией растений, насчитывавшей более 4000 видов.
В 1810 опубликовал труд, посвященный флоре Австралии. В том же году стал личным библиотекарем Дж.Бэнкса. После смерти последнего в 1820 его библиотека и все коллекции перешли по завещанию в пожизненное владение Броуна. В 1827 он передал их Британскому музею и стал хранителем его ботанического отдела. С 1849 по 1853 был президентом Линнеевского общества.
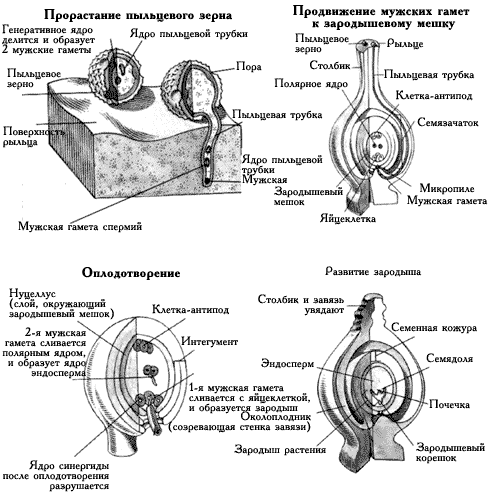
Основные научные работы Броуна посвящены морфологии и систематике растений. Он впервые описал строение семяпочки и установил различие между голосеменными и покрытосеменными растениями (1825), обнаружил процесс полового скрещивания (опыления) у высших растений.
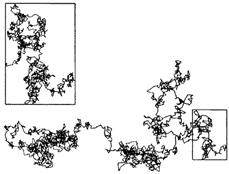
Наблюдая под микроскопом поведение частиц пыльцы, взвешенных в воде, обнаружил, что они совершают хаотические зигзагообразные движения (1827). Впоследствии показал, что подобным образом ведут себя суспензии любых других веществ. Это явление позже получило название броуновского движения. В 1831 Броун изучил и описал ядро растительной клетки.
Умер Броун в Лондоне 10 июня 1858.
Список литературыГенкель П.А. Роберт Броун. – Известия АН СССР, 1959,
Похожие работы
... n — номер шага, а длина их стороны уменьшается как 2–n. Легко показать, что площадь белых пятен равна площади исходного треугольника. Рис.2 Построение салфетки Серпинского Рис.3. Салфетка Серпинского 1.3 Броуновское движение Рассмотренные выше примеры фракталов относятся к так называемым точным фракталам или детерминистическим. Они все построены по вполне определенному ...
ивоє уваги заслуговує той факт, що самі засновники кінетичної теоріі теплоти ніколи не звертались до проблеми броунівського руху. З‘являються нові гіпотези, що до руху мікроскопічних частинок в речовині. Професор фізики фармацевтичної школи в Парижі Жіль Реньо в1858 році після ряду експерементів прийшов до висновку, що броунівський рух пов‘язаний з тепловою дією сонячних променів, що падають ...
... лишь с развитием более тонкой, чем во времена Кельрейтера, микроскопической техники. Поэтому нет ничего удивительного, что в начале XIX в. первые успехи в раскрытии процесса оплодотворения у цветковых растений сделал не ботаник, а крупный специалист в области оптики и микроскопической техники, итальянский ученый, профессор Д.Амичи (1786–1863). Он заведовал в университете своего родного города ...
... ? Ответ: да, такие правила существуют – это уравнения эволюции или динамические уравнения (в частности, ньютоновы законы движения). И все же поведение многих физических объектов, описываемых такими уравнениями, – динамических систем – через какое-то время становится совершенно непредсказуемым. Например, атмосфера – типичная динамическая система, ее эволюция жестко задана известными уравнениями, ...
0 комментариев