Построение траектории Броуновского движения

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РЕСПУБЛИКИ БЕЛАРУСЬ

Учреждение образования

«Брестский государственный университет имени А. С. Пушкина»

Математический факультет

Кафедра информатики и прикладной математики

 

Курсовая работа

ПОСТРОЕНИЕ ТРАЕКТОРИИ БРОУНОВСКОГОДВИЖЕНИЯ

 

Подготовила:

Кондратюк Анна Степановна,

студентка 3 курса специальности

«Математика. Информатика»

Руководитель: Черноокий

Александр Леонидович

Брест 2009

СОДЕРЖАНИЕ

ВВЕДЕНИЕ

1. СЛУЧАЙНЫЕ ФРАКТАЛЫ

1.1 Снежинка Коха

1.2 Салфетка Серпинского

1.3 Броуновское движение

2. СУТЬ БРОУНОВСКОГО ДВИЖЕНИЯ

3. ОПРЕДЕЛЕНИЕ

4. ПРОГРАММИРОВАНИЕ НА DELPHI

4.1 Код программы «Броуновское движение, как хаотичное движение частиц»

4.2 Код программы «Построение траектории броуновское движение»

ЗАКЛЮЧЕНИЕ

ЛИТЕРАТУРА

ВВЕДЕНИЕ

Для того чтобы раскрыть суть броуновского движения необходимо иметь понятие о хаосе и фракталах. Ведь броуновское движение, яркий пример фрактала, который впервые наблюдал в 19 веке шотландский ботаник Роберт Браун. Он же в 1827 году должным образом описал наблюдаемый эффект.

Какими же инструментами располагает теория хаоса? В первую очередь это фракталы.

Мандельброт ввел в употребление термин фрактал, основываясь на теории фрактальной (дробной) размерности Хауодорфа предложенной в 1919 году. Он отыскал нишу для имевших дурную репутацию множеств Кантора, кривых Пеано, функций Вейерштрасса и их многочисленных разновидностей, которые считались нонсенсом. Он и его ученики открыли много новых фракталов, например, фрактальное броуновское движение

Траектории частиц броуновского движения, которым занимались Роберт Броун еще в 1828 году и Альберт Эйнштейн в 1905 году, представляют собой пример фрактальных кривых, хотя их математическое описание было дано только в 1923 году Норбертом Винером. В 1890 году Пеано сконструировал свою знаменитую кривую.

Но в тоже время, как это часто случается в так называемой новой математике, открытия опираются на работы великих математиков прошлого. Исаак Ньютон понимал это, говоря «Если я и видел дальше других, то только потому, что стоял на плечах гигантов».

Изучение фракталов и хаоса открывает замечательные возможности, как в исследовании бесконечного числа приложений, так и в области чистой математики, именно поэтому, этот факт является целью написания данной работы. Здесь описывается суть броуновского движения и траектории, особенности открытия этого явления, определение (с точки зрения теории вероятности) и примеры программирования, что в свою очередь, говорит о возможности применения данного «хаоса» в различных приложениях.

1. СЛУЧАЙНЫЕ ФРАКТАЛЫ

Фрактальные объекты повсеместно встречаются в природе. Это модели снежинок, деревьев, кустов, листьев и тому подобных объектов. Однако фракталы, получаемые с помощью L-систем или СИФ, обладают одним явным недостатком, ограничивающим их применение для моделирования естественных объектов. Они детерминированы.

Построение этих фракталов не сводится к случайным возмущениям детерминированных фракталов. Напротив, случайный характер присущ им изначально, что связано со случайными процессами.

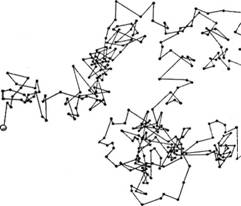
Основной моделью является фрактальное броуновское движение – случайный процесс, широко распространенный в природе.

Некоторые примеры фракталов:

 

1.1 Снежинка Коха

Снежинка Коха представляет собой линию бесконечной длины, ограничивающую конечную площадь, которая в 1.6 раза больше площади образующего ее треугольника.

Пример построения этого фрактала изображен ниже на рис.1.

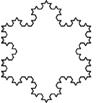
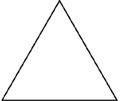
Рис.1.Снежинка Коха

1.2 Салфетка Серпинского

Три первых шага в построении этого фрактала изображены на рис.2, а сам фрактал — на рис.3.

Число треугольных пар все меньшего и меньшего масштаба в нем бесконечно. Число черных треугольников в этом построении растет как 3n, где n — номер шага, а длина их стороны уменьшается как 2–n. Легко показать, что площадь белых пятен равна площади исходного треугольника.

Рис.2 Построение салфетки Серпинского

 

Рис.3. Салфетка Серпинского