Министерство общего и профессионального образования РФ.
Уральский государственный технический университет – УПИ
Кафедра “Технология и средства связи”
"Исследование точности численного интегрирования"
"Research of Accuracy of Numerical Integration"
Отчет
по лабораторной работе
дисциплины
"Информатика",
третий семестр
Преподаватель: Болтаев А.В.
Студенты: Степанов А.Г
Черепанов К.А.
Группа: Р-207
Екатеринбург2000
Содержание
1. Задание исследования.................................................................. 3
2. Подробное описание задачи и способы ее решения................... 3
3. Результаты исследований............................................................. 4
4. Сравнение результатов.............................................................. 12
5. Список библиографических источников................................... 13
6. Текст программы........................................................................ 13
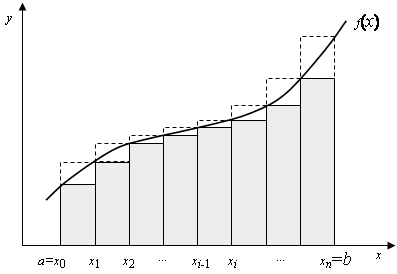
Задание исследования Провести исследование внутренней сходимости численного интегрирования методом Симпсона и трапеций различных функций, задаваемых с помощью языка С. Подробное описание задачи и способы ее решения Необходимо провести исследования так называемой внутренней сходимости численного интегрирования методами Симсона и трапеций различных функций, задаваемых с помощью функций языка С. Предполагается, что отрезок интегрирования [a,b] разбит на n равных частей системой точек (сеткой).![]()
![]()
![]()
![]()
Контроль внутренней сходимости заключается в циклическом вычислении приближенных значений интеграла для удваимого по сравнению со значением на предыдущем прохождении цикла числа n. Отношения абсолютной величины разности этих значений к абсолютной величине предыдущего приближенного значения принимается в качестве критерия достижения точности интеграла.
Построить зависимости количеств итераций от различных величин критерия точности.
Построить обратные зависимости критерия точноти от количества итераций.
Повторить все вышеуказанные исследования для случая, когда при вычислении критерия точности разность значений интеграла относится не к предыдущему значению, а к точному значению аналитически вычисленного интеграла.
Исследовать влияние увеличения верхнего предела интегрирования на точность (при прочих неизменных условиях)
Метод трапеций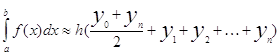 , где
, где
![]()
![]()
Метод Симпсона
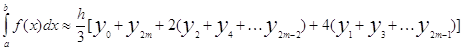 , где
, где
![]()
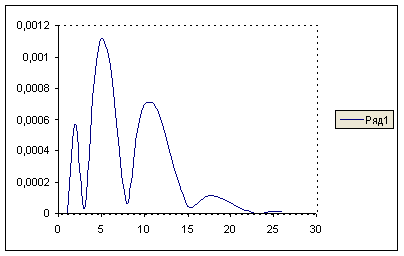
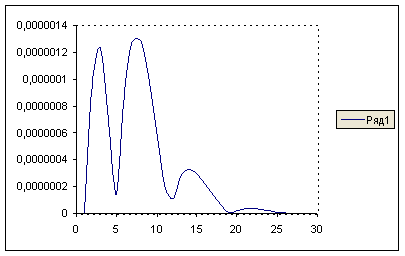
Таблица и график зависимости количества итераций от различных значений критерия точности
Для ![]()
| Критерий точности | Количество итераций |
| -0,1676631 | 14 |
| -0,1518916 | 16 |
| -0,0046931 | 12 |
| -0,0026531 | 11 |
| -0,0002639 | 10 |
| -0,0001709 | 2 |
| -0,0001297 | 9 |
| -0,0000557 | 3 |
| -0,000025 | 8 |
| -0,0000198 | 4 |
| -0,0000096 | 5 |
| -0,0000038 | 6 |
| 0 | 15 |
| 0,0000052 | 7 |
| 0,071089 | 13 |
![]()
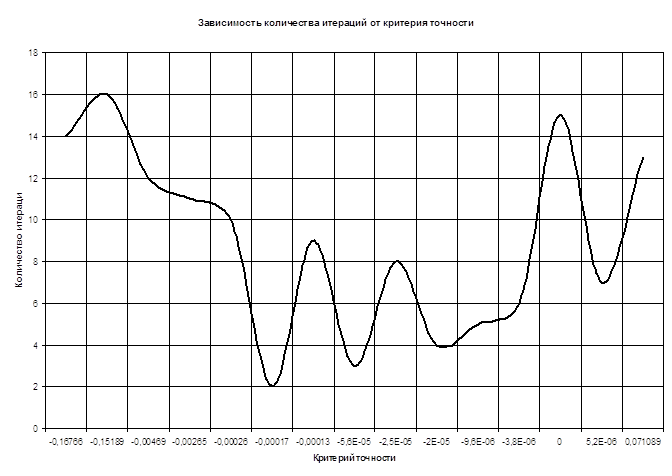
| Критерий точности | Количество итераций |
| -0,1127271 | 16 |
| -0,0750288 | 15 |
| -0,0540677 | 14 |
| -0,0021415 | 12 |
| -0,0005711 | 11 |
| -0,0000458 | 9 |
| -0,0000381 | 2 |
| -0,0000191 | 3 |
| -0,000008 | 4 |
| -0,000004 | 5 |
| -0,0000019 | 7 |
| -0,0000002 | 6 |
| 0,000005 | 8 |
| 0,0002983 | 10 |
| 0,0164377 | 13 |
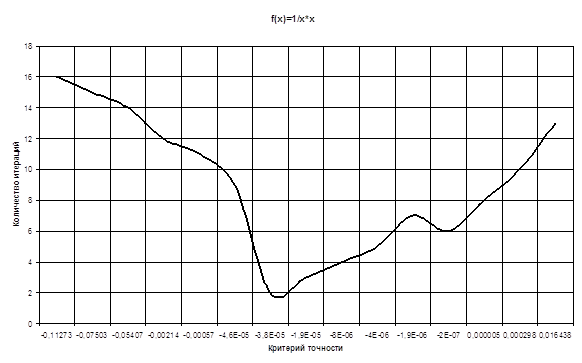 |
![]()
| Критерий точности | Количество итераций |
| -0,0066709 | 13 |
| -0,0042367 | 14 |
| -0,0003561 | 10 |
| -0,0000016 | 5 |
| -0,000001 | 4 |
| 0,0000005 | 3 |
| 0,0000006 | 6 |
| 0,0000009 | 2 |
| 0,0000009 | 7 |
| 0,0000223 | 8 |
| 0,000056 | 9 |
| 0,0002782 | 11 |
| 0,0003474 | 12 |
| 0,005293 | 16 |
| 0,0053267 | 15 |
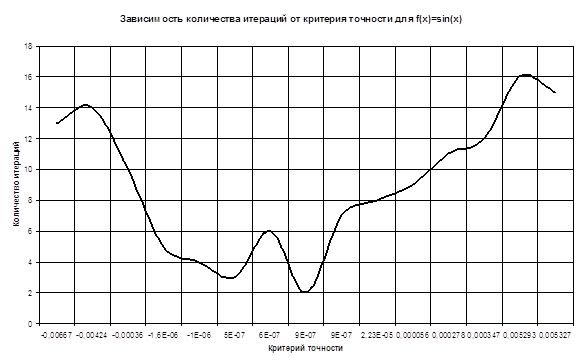 |
![]()
| Критерий точности | Критерий точности |
| -61,4469795 | 12 |
| -5,714047 | 3 |
| -1,0215755 | 13 |
| -0,7241433 | 2 |
| -0,5121117 | 4 |
| -0,3222643 | 11 |
| -0,2163614 | 7 |
| -0,1536629 | 9 |
| -0,0930261 | 14 |
| 0,0353183 | 16 |
| 0,057059 | 15 |
| 0,1697371 | 5 |
| 0,2025534 | 10 |
| 0,2504728 | 6 |
| 0,6202592 | 8 |
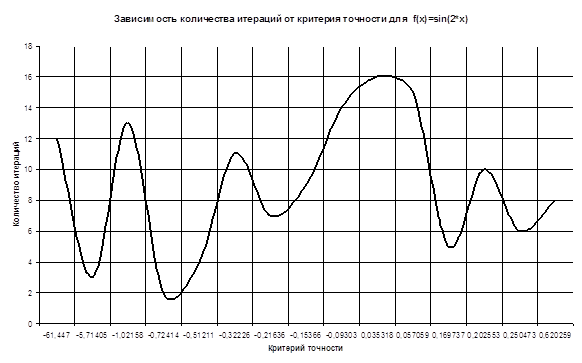 |
![]()
| Критерий точности | Количество итераций |
| -0,0119308 | 16 |
| -0,0007834 | 13 |
| -0,0000079 | 3 |
| -0,0000041 | 4 |
| -0,0000037 | 7 |
| -0,0000027 | 5 |
| -0,0000027 | 6 |
| -0,000002 | 8 |
| -0,0000016 | 2 |
| 0,0000003 | 10 |
| 0,0000062 | 9 |
| 0,0000385 | 11 |
| 0,0000802 | 12 |
| 0,0005452 | 15 |
| 0,0016689 | 14 |
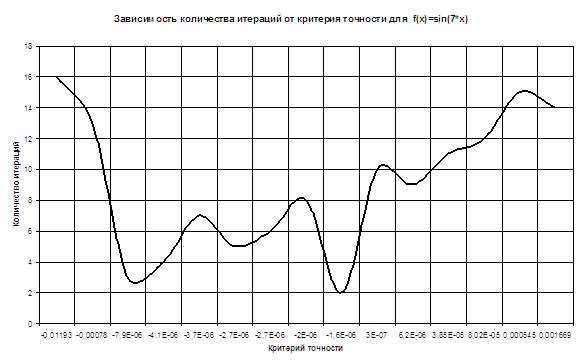 |
![]()
| Критерий точности | Количество итераций |
| -0,0026286 | 16 |
| -0,0012416 | 14 |
| -0,0000118 | 3 |
| -0,0000107 | 4 |
| -0,0000046 | 5 |
| -0,0000046 | 9 |
| -0,0000028 | 6 |
| -0,0000021 | 7 |
| -0,0000005 | 2 |
| 0,0000011 | 10 |
| 0,0000018 | 8 |
| 0,0000023 | 11 |
| 0,000058 | 12 |
| 0,0001049 | 13 |
| 0,0027928 | 15 |
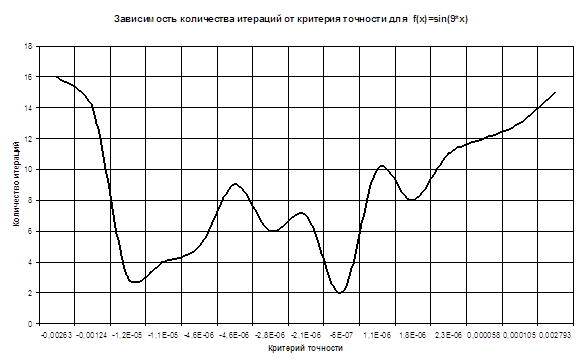
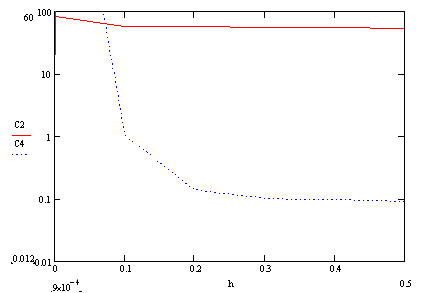
Таблица и график зависимости значений критерия точности от количества итераций
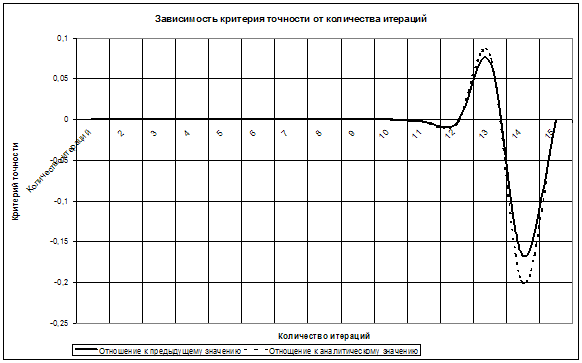
Для функции ![]()
| По отношению к предыдущему значению | По отношению к аналитическому значению | ||||
| Критерий точности | Количество итераций | Критерий точности | Количество итераций | ||
| -0,0001709 | 2 | -0,0001932 | 2 | ||
| -0,0000557 | 3 | -0,0000629 | 3 | ||
| -0,0000198 | 4 | -0,0000224 | 4 | ||
| -0,0000096 | 5 | -0,0000108 | 5 | ||
| -0,0000038 | 6 | -0,0000043 | 6 | ||
| 0,0000052 | 7 | 0,0000058 | 7 | ||
| -0,000025 | 8 | -0,0000283 | 8 | ||
| -0,0001297 | 9 | -0,0001466 | 9 | ||
| -0,0002639 | 10 | -0,0002983 | 10 | ||
| -0,0026531 | 11 | -0,002998 | 11 | ||
| -0,0046931 | 12 | -0,0052891 | 12 | ||
| 0,071089 | 13 | 0,0797403 | 13 | ||
| -0,1676631 | 14 | -0,2014365 | 14 | ||
| 0 | 15 | 0 | 15 | ||
| -0,1518916 | 16 | -0,1518916 | 16 | ||
 |
Для функции ![]()
| По отношению к предыдущему значению | По отношению к аналитическому значению | ||||||||
| Критерий точности | Количество итераций | Критерий точности | Количество итераций | ||||||
| -0,0000381 | 2 | -0,0000666 | 2 |
| ||||||
| -0,0000191 | 3 | -0,0000335 | 3 |
| ||||||
| -0,000008 | 4 | -0,0000141 | 4 |
| ||||||
| -0,000004 | 5 | -0,0000069 | 5 |
| ||||||
| -0,0000002 | 6 | -0,0000004 | 6 |
| ||||||
| -0,0000019 | 7 | -0,0000033 | 7 |
| ||||||
| 0,000005 | 8 | 0,0000088 | 8 |
| ||||||
| -0,0000458 | 9 | -0,0000802 | 9 |
| ||||||
| 0,0002983 | 10 | 0,000522 | 10 |
| ||||||
| -0,0005711 | 11 | -0,0009997 | 11 |
| ||||||
| -0,0021415 | 12 | -0,0037465 | 12 |
| ||||||
| 0,0164377 | 13 | 0,0286955 | 13 |
| ||||||
| -0,0540677 | 14 | -0,0959378 | 14 |
| ||||||
| -0,0750288 | 15 | -0,1259331 | 15 |
| ||||||
| -0,1127271 | 16 | -0,1750124 | 16 |
| ||||||
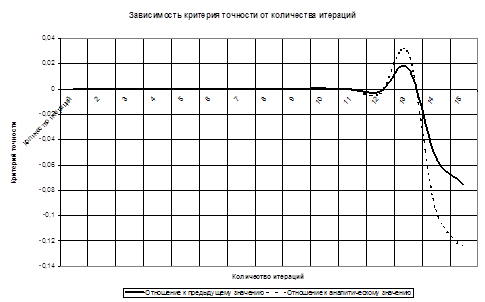
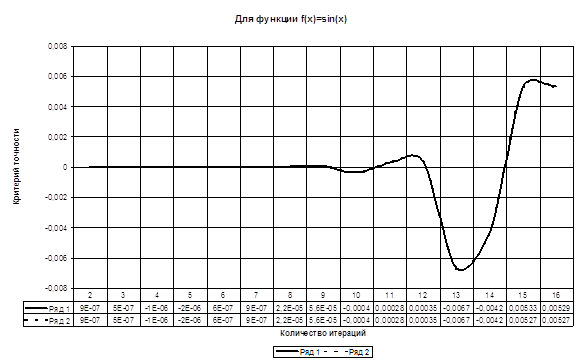
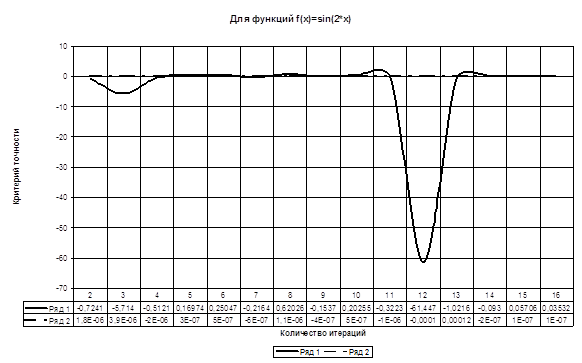
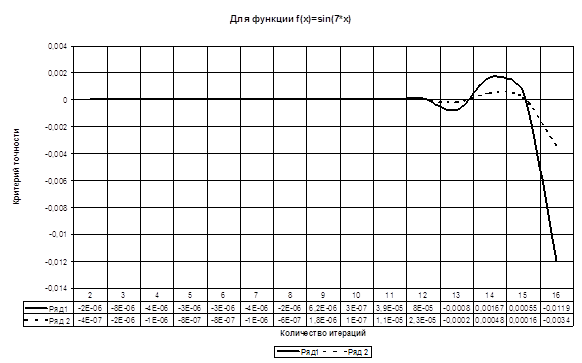
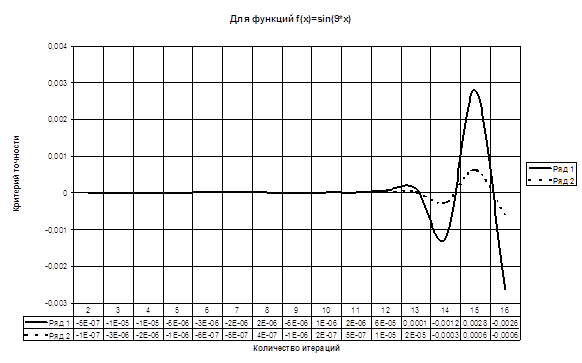
Таблица сравнительных результатов
| Метод трапеции n=1000000 | Метод Симпсона n =1000000 | Аналитический результат | Функция | Пределы |
| 4,5051475 | 4,5240183 | 4,49980967 | f(x)=1/x | 0,1…..9 |
| 1,7491462 | 1,7500761 | 1,791756469 | f(x)=1/x*x | 0,3…..5 |
| 1,9991885 | 1,9999505 | 2 | f(x)=sin(x) | 0…….π |
| -0,0000512 | 0,000003 | 0 | f(x)=sin(2*x) | 0…….π |
| 0,2857157 | 0,2856935 | 0,285714285 | f(x)=sin(7*x) | 0…....π |
| 0,2222053 | 0,2222133 | 0,222222222 | f(x)=sin(9*x) | 0…....π |
| Аналитическое значение | Практическое значение | Верхний предел | Погрешность |
| 4,49980967 | 4,5217996 | 9 | -0,02198993 |
| 4,605170186 | 4,624969 | 10 | -0,019798814 |
| 4,787491743 | 4,8039412 | 12 | -0,016449457 |
| 4,941642423 | 4,9557843 | 14 | -0,014141877 |
| 5,075173815 | 5,0875444 | 16 | -0,012370585 |
| 5,192956851 | 5,2039275 | 18 | -0,010970649 |
| 5,298317367 | 5,3082042 | 20 | -0,009886833 |
Следовательно, увеличение верхнего предела приводит к увеличению точности интегрирования
Список библиографических источников1. Справочник по математике/Бронштейн И.Н., Семендяев К.А.-М.:Физико-математическая литература, 1998.
Текст программы/* Курсовая работа по информатике
"Исследование точности численного интегрирования"
"Research of Accuracy of Numerical Integration"
Преподаватель:
Студенты: Степанов А.Г.
Черепанов К.А.
Группа: Р-207
*/
# include <stdio.h>
# include <io.h>
# include <stdlib.h>
# include <iostream.h>
# include <string.h>
# include <math.h>
int main ()
{
FILE *fp; /*указатель на поток*/
int n,i,t,j,N;
float a,b,h,Sum[100],x,y,coa;
printf("Research of Accuracy of Numerical Integration\n");
/*Ввод точности вычисления*/
printf("Enter accuracy of calculation n= ");
scanf("%d",&n);
/*Ввод начала интегрирования*/
printf("Enter beginnings of integration= ");
scanf("%f",&a);
/*Ввод предела интегрирования*/
printf("Enter limit of integration= ");
scanf("%f",&b);
/*Открытие файла-источника*/
while((fp=fopen("data3.xls","w"))==NULL)
{
puts("Error!!! Can't open file \nInput name of file\n");
}
/*Ввод количества итераций*/
printf("Enter number of Itteration N= ");
scanf("%d",&N);
/*Вычисление шага интегрирования*/
h=(a+b)/n;
printf("Step=%.3f\n",h);
/*******Вычисление интеграла методом трапеций*******/
for(j=1;j<=N;j++)
{
h=(a+b)/(int(pow(2,j-1))*n);
Sum[j]=0;
for(i=0;i<=(int(pow(2,j-1))*n);i++)
{
x=a+i*h;
if(i==0)
t=1;
else
t=2;
y=t*(h/2)*(sin(2*x));
Sum[j]=Sum[j]+y;
}
if (j>1)
{
coa=(Sum[j]-Sum[j-1])/Sum[j-1];
printf("Criterion of accuracy=%.5f Number of iteration=%d\n",coa,j);
fprintf(fp,"%.7f\t",coa);
fprintf(fp,"%d\t\n",j);
}
}
printf("The sum by a method of trapezes=%.7f\n",Sum[1]);
fprintf(fp,"The sum by a method of trapezes=%.7f\n",Sum[1]);
/*******Вычисление интеграла методом Симпсона*******/
for(j=1;j<=N;j++)
{
h=(a+b)/(int(pow(2,j-1))*n);
Sum[j]=0;
for(i=0;i<=(int(pow(2,j-1))*n);i++)
{
x=a+i*h;
if(i==0||i==n)
t=1;
else
{
if(i%2==0)
t=2;
else
t=4;
}
y=t*(h/3)*(sin(2*x));
Sum[j]=Sum[j]+y;
}
if (j>1)
{
coa=(Sum[j]-Sum[j-1])/Sum[j-1];
printf("Criterion of accuracy=%.5f Number of iteration=%d\n",coa,j);
fprintf(fp,"%.7f\t",coa);
fprintf(fp,"%d\t\n",j);
}
}
printf("The sum by a Simpson's method= %.7f\n",Sum[1]);
fprintf(fp,"The sum by a Simpson's method=%.7f\n",Sum[1]);
scanf("%d",&b);
}
Похожие работы
... . Также мы получим графическое отображение процесса интегрирования на участках возрастания и убывания функции. 2. Выбор математической модели задачи Кратко рассмотрим основные методы численного интегрирования и выясним почему метод Гаусса наиболее подходит для решения нашей задачи. 2.1 Метод прямоугольников Метод прямоугольников получается при замене подынтегральной функции на ...
... - 0.588. 2. Математические и алгоритмические основы решения задачи Кратко рассмотрим основные методы численного интегрирования и выясним, почему самый лучший и быстрый метод интегрирования - десятиточечный метод Гаусса. 2.1 Метод прямоугольников Метод прямоугольников получается при замене подынтегральной функции на константу. В качестве константы можно взять значение функции в любой ...
... – остаточный член, характеризующий погрешность формулы. Заметим, что формулы вида (2) называют квадратурными формулами. Геометрический смысл численного интегрирования состоит в вычислении площади криволинейной трапеции, ограниченной графиком функции f(х), осью абсцисс и двумя прямыми х = а и х = b. Приближенное вычисление площади приводит к отбрасыванию в квадратурных формулах остаточного члена ...
... для курсовой работы, заключающегося в интегрирования ОДУ, была составлена и отлажена программа, приведенная в приложении А. С помощью данной программы проведена серия опытных исследований свойств методов Рунге-Кутты второго и четвёртого порядков. При задании определенного интервала значений шага интегрирования ошибка интегрирования уменьшается с уменьшением шага. Подтверждение сего факта можно ...



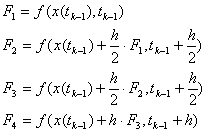
0 комментариев