Навигация
Численное интегрирование функций
Содержание
численное интегрирование формула программирование
Введение 1. Методы численного интегрирования2. Квадратурные формулы
3. Автоматический выбор шага интегрирования
Заключение
Библиографический списокВведение
Цель реферата состоит в изучение и сравнительный анализ методов численного интегрирования функций; реализация этих методов в виде машинных программ на языке высокого уровня и практическое решение задач численного интегрирования на ЭВМ.
При решении инженерных задач часто возникает необходимость в вычислениях значений определенного интеграла вида
![]() . (1)
. (1)
Если функция непрерывна на отрезке [a, b] и ее первообразная может быть определена через известную функцию, то вычисление такого интеграла производится по формуле Ньютона – Лейбница:
![]() .
.
В инженерных задачах получить значение интеграла в аналитическом виде удается редко. Кроме того, функция f(x) может быть задана, например, таблицей экспериментальных данных. Поэтому на практике для вычисления определенного интеграла используют специальные методы, в основе которых лежит аппарат интерполирования.
Идея таких методов заключается в следующем. Вместо того, чтобы вычислять интеграл по формуле (1), сначала вычисляют значения функции f(xi) = yi в некоторых узлах xi Î[a, b]. Затем выбирается интерполяционный многочлен P(x), проходящий через полученные точки (xi, yi), который используется при вычислении приближенного значения интеграла (1):
![]() .
.
При реализации такого подхода формулы численного интегрирования принимают следующий общий вид:
![]() , (2)
, (2)
где ![]() - узлы интерполирования, Ai – некоторые коэффициенты, R – остаточный член, характеризующий погрешность формулы. Заметим, что формулы вида (2) называют квадратурными формулами.
- узлы интерполирования, Ai – некоторые коэффициенты, R – остаточный член, характеризующий погрешность формулы. Заметим, что формулы вида (2) называют квадратурными формулами.
Геометрический смысл численного интегрирования состоит в вычислении площади криволинейной трапеции, ограниченной графиком функции f(х), осью абсцисс и двумя прямыми х = а и х = b. Приближенное вычисление площади приводит к отбрасыванию в квадратурных формулах остаточного члена R, характеризующего погрешность метода, на которую дополнительно накладывается вычислительная погрешность.
1. Методы численного интегрирования
В прикладных исследованиях часто возникает необходимость вычисления значения определённого интеграла
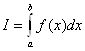
Как известно из курса математики, аналитически вычисление интеграла можно провести не во всех случаях. И даже в том случае, когда удаётся найти аналитический вид этого интеграла, процедура вычисления даёт приближённый результат, поэтому возникает задача приближенного значения этого интеграла.
![]()
Суть приближенного вычисления заключается в двух операциях: 1. в выборе конечного числа вместо n; 2. в выборе точки ![]() в соответствующем отрезке.
в соответствующем отрезке.
В зависимости от выбора ![]() мы получаем различные формулы для вычисления интеграла: Формулы левых и правых прямоугольников (5), (6)
мы получаем различные формулы для вычисления интеграла: Формулы левых и правых прямоугольников (5), (6)
![]() (5)
(5)
![]() (6)
(6)
Формула трапеции:
![]()
Формула Симпсона
![]()
где m=n/2
h=b-a/n
b, a - концы рассматриваемого отрезка.
Для сравнения результатов вычисления вышеизложенными формулами численного интегрирования вычислим 3-мя способами следующий интеграл, разделив отрезок [0, ![]() ] на 6 равных отрезков:
] на 6 равных отрезков:
![]() h=
h=![]()
По формуле левых прямоугольников:
![]()
По формуле трапеции:
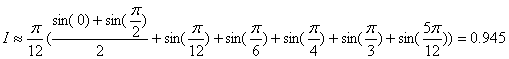
По формуле Симпсона:
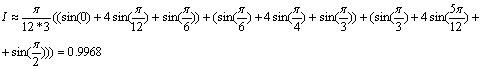
А результат полученный аналитически равен
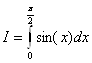 =1
=1
Следовательно, можно сделать вывод о том, что численный метод интегрирования по формуле Симпсон является более точным, но используется в общем случае при делении рассориваемого отрезка на чётное число промежутков.
Похожие работы
... . Также мы получим графическое отображение процесса интегрирования на участках возрастания и убывания функции. 2. Выбор математической модели задачи Кратко рассмотрим основные методы численного интегрирования и выясним почему метод Гаусса наиболее подходит для решения нашей задачи. 2.1 Метод прямоугольников Метод прямоугольников получается при замене подынтегральной функции на ...
... - 0.588. 2. Математические и алгоритмические основы решения задачи Кратко рассмотрим основные методы численного интегрирования и выясним, почему самый лучший и быстрый метод интегрирования - десятиточечный метод Гаусса. 2.1 Метод прямоугольников Метод прямоугольников получается при замене подынтегральной функции на константу. В качестве константы можно взять значение функции в любой ...
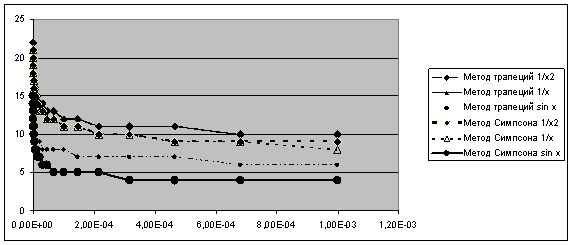
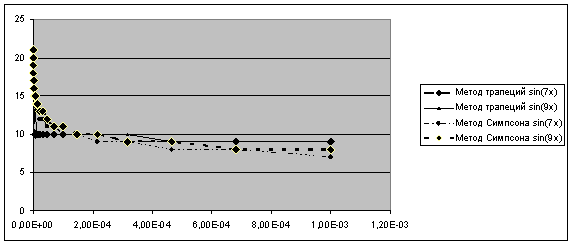
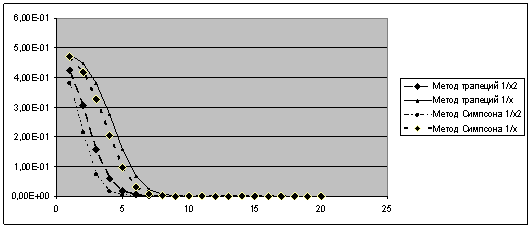
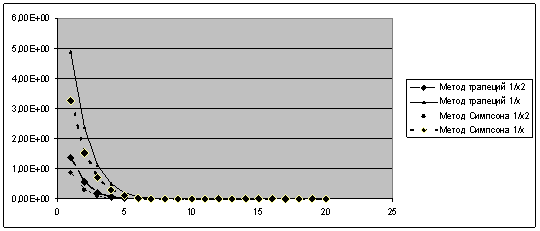
... и методика испытаний 5.1 Объект испытаний Объектом испытаний является программа, предназначенная для исследования внутренней сходимости численного интегрирования с помощью методов вычисления интегралов: методы трапеций и Симпсона. 5.2 Цель испытаний Целью испытаний является проверка точности работы программы для данной задачи. 5.3 Требования к программе Во время испытаний ...
... производной: diff (f (х) , х$3). Пример 1. Вычисление производных. > s:=x^3*cos(x)+y^2*ln(sin(x)); > diff(s,x); > diff(s,x$2); > diff(s,x,y); > fs:=Diff(s,x); > q:=sqrt(fs); > value(%); Последние три команды показывают использование отложенной формы команды дифференцирования. 2. Интегрирование выражений Команда int( ) имеет отложенную форму ...
0 комментариев