Навигация
Формирование уравнений математической модели фильтра
2. Формирование уравнений математической модели фильтра.
Более универсальным в задачах исследования, разработок является метод переменных состояния, отличительной особенностью и достоинством которого является возможность получения ММ в так называемой форме Коши (уравнения относительно производных), что позволяет использовать базовые программы математического обеспечения ЭВМ. Метод переменных состояний является базовым методом в САПР устройств, систем, сетей радиосвязи.
Суть метода состоит в том, что анализируемая RLC- цепь может представлена в виде: пассивной линейной R-цепи из которой выносятся реактивные элементы и независимые источники входных воздействий. Далее реактивные элементы и независимые источники представляются, как вектор состояния X(t) и вектор воздействия Xни(t) анализируемой цепи. Тогда полная система уравнений математической модели анализируемой цепи будет иметь вид:
Iрез(t)=В1X(t)+B2Xни(t) (I),
dX(t)/dt=P1(t)+P2Xни(t) (2),
Xвых(t)=Dl X(t)+ D2Xни(t) (3),
где
(1) - уравнение токов резистивных элементов, Bl, B2 -матричные коэффициенты, значение которых определяется топологией и сопротивлениями резистивных элементов R-цепи.
(2) - уравнение состояния, Р1,Р2-матричные коэффициенты, значения которых зависит от топологии цепи и параметров ее элементов;
(3) - уравнение выхода в котором скаляр Хвыx.(t) обозначает напряжение Uвых. либо ток Iвых. для выделенного при анализе выхода схемы, а коэффициенты D1,D2 определяются данными схемы.
Алгоритм решения системы (1) - (3) основан на следующей последовательности действий:
· первоначально решаются уравнения (2) (при этом порядок уравнения, то есть число уравнений, объединенных в матричное выражение (2), определяется числом элементов вектора Х);
· по найденному значению Х рассчитывается вектор Iрез. из
уравнения (1);
· для известных значений Х и Iрез. находится значение
скаляра Хвых(t).
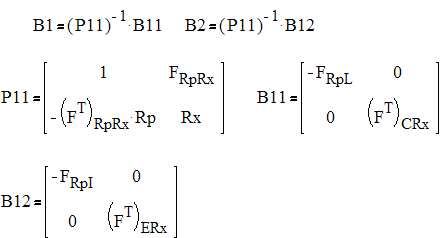 |
Значение коэффициентов В1, В2, Р1, Р2 находятся в результате преобразования топологических уравнений анализируемой цепи.

где FCL, FERx и т.п. -подматрицы МГС.
Для получение матрицы главных сечений необходимо преобразовать редуцированую матрицу цепи.
 |
Запишем редуцированную матрицу:
 |
В результате преобразований получим матрицу главных сечений:
Выделим подматрицы из МГС
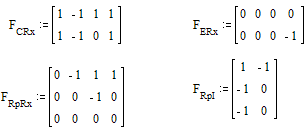
Определим коэффициенты В1, В2, Р1, Р2, используя для этого программу “Mathcad”.
Составим необходимые транспонированые подматрицы
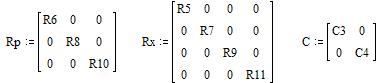 |
Составим
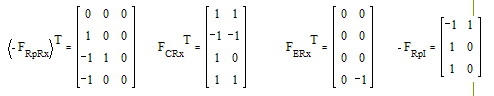
матрицу сопротивлений Rp и Rx, а также матрицу ёмкостей C
Подставляя полченные матрицы в вышеприведённые формулы получим:

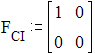 |
Для определения коэффициентов P1 и P2 составим подматрицу МГС Fci:

Тогда
3.Разработка блок - схемы алгоритма и программы формирования матрицы главных сечений.

Рис. 4. Блок-схема алгоритма программы формирования МГС.
Program MATR;
const k=30;
var n,m,i,j,c,r,e,Ii,s,l,G,z,y,p,q,d:integer;
STM:array[1..k,1..k] of integer;
PR:array[1..k] of integer;
b:array[1..k] of integer;
MGS,FERx,FCRx,FRpRx,FEL,FCL,FRpL,FEI,FCI,FRpI:array[1..k,1..k] of integer;
{ Процедура ввода структурной матрицы ипараметров схемы.}
procedure strm;
begin
writeln;
write(' ‚Введите количество узлов n=');
read(n);
write(' ‚ Введите количество ветвей m=');
read(m);
write(' ‚ Введите последовательно количество элементов схемы E,C,R,L,I.');
writeln;
write(' E='); read(e);
write(' C='); read(c);
write(' R='); read(r);
write(' L='); read(l);
write(' I='); read(Ii);
write('‚Введите элементы структурной матрицы СТРМ[i,j]=1,-1,0 если j ветвь');
writeln(втекает в i узел то СТРМ[i,j]=1, если вытекает то -1, если не подключен -0.');
for i:=1 to n do
begin writeln;
for j:=1 to m do
begin
write(' СТРМ[',i,'узел,',j,'ветвь]='); read(STM[i,j]);
end;
end;
{Вывод на экран структурной матрицы}
write(' СТРМ');
for i:=1 to n do
begin writeln;
for j:=1 to m do
write(STM[i,j]:3);
end;
end;
procedure sea;
begin
writeln;
write(' Для прлолжения программы нажмите ENTER . ');
readln;
end;
{”Формирование МГС из структурной матрицы.}
procedure MGSS;
begin
for s:=1 to n do begin i:=s;j:=s;
while i<=n do begin while j<=m do begin if STM[i,j]<>0 then begin
p:=i;g:=j;i:=n;j:=m end;j:=j+1 end;i:=i+1 end;
if p>s then for j:=1 to m do begin PR[j]:=STM[s,j];
STM[s,j]:=STM[p,j];
STM[p,j]:=PR[j] end;
if g<>s then begin
for i:=1 to n do b[i]:=STM[i,g];
for j:=g downto s+1 do
for i:=1 to n do STM[i,j]:=STM[i,j-1];
for i:=1 to n do STM[i,s]:=b[i] end;
if STM[s,s]=-1 then for j:=s to m do STM[s,j]:=-STM[s,j];
for i:=1 to n do begin if i<>s then begin
if STM[i,s]=1 then for j:=s to m do STM[i,j]:=STM[s,j]-STM[i,j];
if STM[i,s]=-1 then for j:=s to m do STM[i,j]:=STM[s,j]+STM[i,j] end;end;
end;
writeln('Матрица главных сечений');
for i:=1 to n do for j:=1 to m-s do MGS[i,j]:=STM[i,j+s];
for i:=1 to n do begin writeln;for j:=1 to m-s do begin
if MGS[i,j]=-1 then write(' ',MGS[i,j]);
if MGS[i,j]<>-1 then write(' ',MGS[i,j]) end;end;end;
{Формирование подматриц из МГС‘}
procedure MGS2;
begin
s:=r+e+c-n;
for i:=1 to e do {Выделение Ferхорд}
for j:=1 to s do
FERx[i,j]:=MGS[i,j];
for i:=e+1 to e+c do { Выделение Fcrхорд}
for j:=1 to s do
FCRx[i-e,j]:=MGS[i,j];
for i:=e+c+1 to n do { Выделение Fребер rхорд}
for j:=1 to s do
FRpRx[i-e-c,j]:=MGS[i,j];
for i:=1 to e do { Выделение Fel}
for j:=s+1 to s+l do
FEL[i,j-s]:=MGS[i,j];
for i:=e+1 to e+c do { Выделение Fcl}
for j:=s+1 to s+l do
FCL[i-e,j-s]:=MGS[i,j];
for i:=e+c+1 to n do { Выделение Frреберl}
for j:=s+1 to s+l do
FRpL[i-e-c,j-s]:=MGS[i,j];
for i:=1 to e do { Выделение Fei}
for j:=s+l+1 to s+l+Ii do
FEI[i,j-s-l]:=MGS[i,j];
for i:=e+1 to e+c do { Выделение Fci}
for j:=s+l+1 to s+l+Ii do
FCI[i-e,j-s-l]:=MGS[i,j];
for i:=e+c+1 to n+1 do { Выделение Frреберi}
for j:=s+l+1 to s+l+Ii do
FRpI[i-e-c,j-s-l]:=MGS[i,j];
end;
begin
strm;
sea;
MGSS;
sea;
MGS2;
write('FERx');
for i:=1 to e do
begin writeln;
for j:=1 to s do
write(FERx[i,j]:4);
end;
sea;
write('FCRx');
for i:=1 to c do
begin writeln;
for j:=1 to s do
write(FCRx[i,j]:4);
end;
sea;
write('FRpRx');
for i:=1 to n-e-c do
begin writeln;
for j:=1 to s do
write(FRpRx[i,j]:4);
end;
sea;
write('FEL');
for i:=1 to e do
begin writeln;
for j:=1 to l do
write(FEL[i,j]:4);
end;
sea;
write('FCL');
for i:=1 to c do
begin writeln;
for j:=1 to l do
write(FCL[i,j]:4);
end;
sea;
write('FRpL');
for i:=1 to n-1-e-c do
begin writeln;
for j:=1 to l do
write(' ',FRpL[i,j],' ');
end;
sea;
write('FEI');
for i:=1 to e do
begin writeln;
for j:=1 to Ii do
write(FEI[i,j]:4);
end;
sea;
write('FCI');
for i:=1 to c do
begin writeln;
for j:=1 to Ii do
write(FCI[i,j]:4);
end;
sea;
write('FRpI');
for i:=1 to n-e-c do
begin writeln;
for j:=1 to Ii do
write(FRpI[i,j]:4);
end;
sea;
end.
4.Расчет коэффициентов уравнения выхода.
Для расчета коэффициентов D1, D2 уравнения выхода в случае, когда Xвых.(t)=Uвых(t), выходной отклик цепи можно представить в виде алгебраической суммы напряжений ветвей при обходе некоторого контура от начальной выходной клеммы к конечной.
В том случае когда выходное напряжения снимается с резистивного элемента, формирование коэффициентов может быть представлено в виде некоторого алгоритма представленного ниже.
Алгоритм расчета коэффициентов:
1. D1 - определяется как к-я строка коэффициента В1, где к-порядковый номер элемента в соответствующем векторе Iрез;
2. D2-определяется как элемент b[k,i] из коэффициента В2, где i-порядковый номер входного источника в векторе Xни.
3. Если Xвых=U[Rk] коэффициенты D1=D1*Rk, D2=D2*Rk.
На основание выше всего изложенного рассчитаем коэффициенты D1, D2:

k=4, i=2.
5.Формирование системы линейных уравнений для расчета частотных характеристик, разработка алгоритма программы.
Для анализа частотных характеристик цепи достаточно воспользоваться уравнением состояния (1) и выхода(3). Предполагая характер входного воздействия гармонической функцией времени и записывая Хни(t) как Хвх(t),
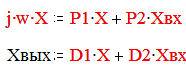 запишем эти уравнения в комплексной форме:
запишем эти уравнения в комплексной форме:
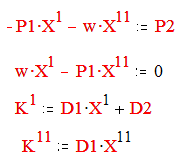
Полагая Хвх = 1 можно определить Хвых = К*Хвх. Представляя переменные Х и К в развернутой форме и приводя подобные, получим следующею систему уравнений позволяющую рассчитать действительную и мнимую части комплексного коэффициента передачи:
Распишем эту систему конкретно для нашего случая, и получим следующий результат:
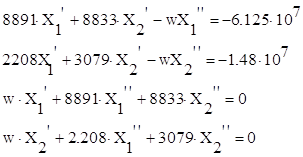
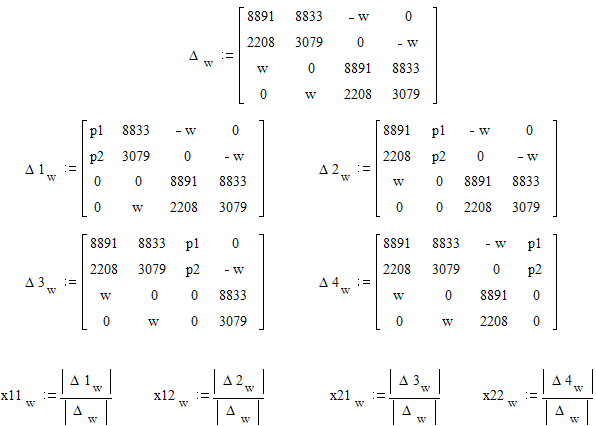
Решим эту систему методом Крамера
где p1= -6.152^7 и p2= -1.48^7.![]()
![]()
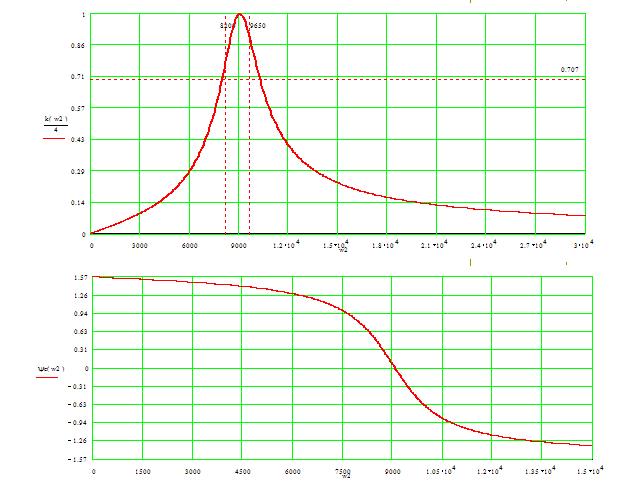
[X1] АЧХ и ФЧХ строятся по следующим формулам
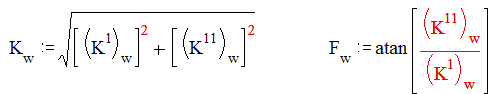
Рис. 5. АЧХ и ФЧХ проектируемой цепи.
6.Расчет частотных характеристик с использованием пакета
«Electronics Workbench Pro».
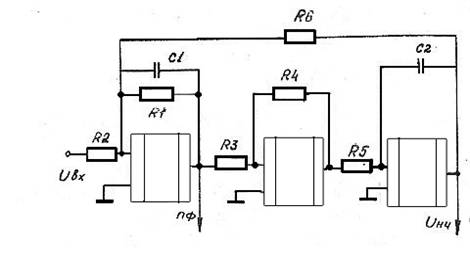
В данном пакете была спроектирована схема полосового фильтра.
И были получены следующие результаты:
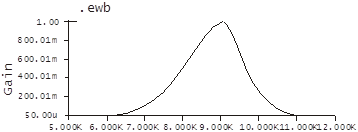 |
АЧХ
 |
ФЧХ
7. Заключение.
В ходе выполненной работы пришли к следующим результатам:
1. Была проверена правильность выбора схемы и её расчёта с помощью новейшего пакета компьютерного моделирования электронных схем “Electronics Workbench Pro” .
2. Для убеждения в правильности расчёта схемы, расчёты также проводились в программе “Mathcad”. В результате были получены зависимости АЧХ и ФЧХ от частоты, изображенные на рис. 5.
3. На основе полученных результатов можно сказать, требуемая перед нами цель была выполнена. Есть некоторые различия, но они обусловлены погрешностью математических вычислений.
8. Список используемой литературы.
1. Мошиц Г., Хорн П. “Проектирование активных фильтров”.
2. Калабеков Б.А. и др. “Методы автоматизированного расчета электронных схем.”.
3. Конспект лекций.
[X1]
Похожие работы
... даже иногда вредным. Однако превратить УПТ в усилитель переменного тока можно достаточно просто (например, вводя разделительные емкости). Поэтому большинство массовых операционных усилителе выпускаются как усилители постоянного тока. Условное обозначение ОУ приведено на рисунке 7.1. В обозначении функции (¥ > – усилитель с бесконечно большим коэффициентом усиления) первый символ (¥) ...
... n = 2. По таблицам приложения определяем полюсы низкочастотной аппроксимирующей функции и количество активных резонаторов. Количество резонаторов – 4. Рассчитаем добротность полосового фильтра Вычислим параметры y и r и добротность активных резонаторов. Где Re и Im – действительная и мнимая части полюсов резонаторов. Вычислим добротность резонаторов Определим ...
... доступны. 5. Низкочастотные фильтры можно построить на элементах малых номиналов. Целью данной курсовой работы является проектирование активного фильтра высоких частот основанного на интегральных операционных усилителях. 1. Существующие виды активных ВЧ фильтров Рассмотрим методы реализации различных типов функций цепи, основанные на использовании схем фильтров, включающих как активные, ...
... . 5. Получены длительные непрерывные ряды наблюдений интенсивности потока и азимутальных распределений СДВ атмосфериков, которые позволили проследить динамику грозовой активности в мировых грозовых центрах. 5.1. Морской мониторинг показал, что основной вклад в мировую грозовую активность дают континентальные и островные грозовые центры. Вариации интенсивности потока импульсов хорошо ...


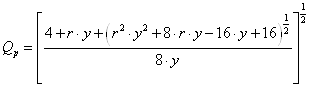

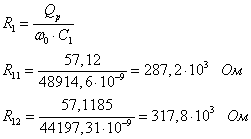
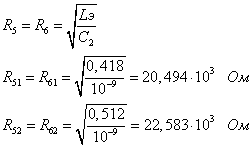
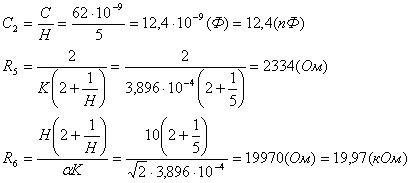
0 комментариев