Графическое определение p-множества

2.2. Графическое определение p-множества

Сначала необходимо построить график.

Для построения графика необходимы следующие данные:

исходные данные:

L₁ = x₁ - 2x₂ + 2,

L₂ = x₁ + x₂ + 4,

L₃ = -x₁ + 4x₂ - 20,

в каноническом виде (после подстановки точки (5;3))

d¹ = x₁ - 2x₂ + 1, (5 - 2*3 + 1= 1)

D_x^k d² = x₁ + x₂ - 8, (5 + 3 + 4 = 12)

d³  = -x₁ + 4x₂ - 7, (-5 + 4*3 - 20 = -13)

D = 2x₁ + 4x₂ – 14,

Находим точки для построения прямых:

1)  d¹ = x₁ - 2x₂ + 1,

-x₁ + 2x₂ £ 1 (1;1)

2)  d² = x₁ + x₂ - 8,

x₁ + x₂ ³ 8 (0;8)

3)  d³  = -x₁ + 4x₂ - 7,

-x₁ + 4x₂ ³ 7 (1;2)

По полученным точкам строим график (рисунок 1). На рисунке штриховкой показан полученный д-конус. Переход к любой точке внутри конуса обеспечивает увеличение всех критериев. Точка (29/3; 16/3) является p-оптимальным решением. Смещая точку х^, внутрь д-конуса придем на границу e₁. При этом д-конус выйдет из области допустимых решений (ОДР) D_x. Теперь полученная точка не сможет улучшить ни один ч-критерий без ухудшения других, значит она p-оптимальная. Построив д-конус в любой точке стороны e₁, убеждаемся, что каждая из точек p-оптимальна, значит вся сторона e₁ составляет p-множество.

3.Определение Парето-оптимального множества

с-методом

 

3.1.Удаление пассивных ограничений

Перед построением p-множества из системы ограничений должны быть удалены пассивные ограничения. Пассивным будем называть неравенство (п-неравенство), граница которого не является частью границ области D_x, за исключением, может быть, ее отдельной точки. Неравенства, образующие границы D_x, назовем активными (а-неравенства).

Чтобы грани не были включены в D_x^p, не имея никакого отношения к D_x^p, неравенство e₁ должно быть удалено из исходной системы ограничений. Условием для исключения неравенства e_i³ 0 из системы является несовместность (или вырожденность) данной системы неравенств при условии e_i = 0. Геометрически это означает, что граница e_i = 0 неравенства e_i ³ 0 не пересекается с областью D_x или имеет одну общую точку. Если граница e_i = 0 имеет общую угловую точку с D_x (вырожденность), то с удалением п-неравенства e_i ³ 0 эта точка не будет утеряна, так как она входит в границы других неравенств. Помимо заданных m неравенств проверке подлежат и n условий неотрицательности переменных, так как координатные плоскости (оси) также могут входить в границы D_x.

В качестве примечания можно отметить, что поскольку п-неравенства (пассивные неравенства) для любой точки x Î D_x будут выполнены, то по мере выявления п-неравенств и введения их в базис они удаляются из с-таблицы.

Запишем систему неравенств D_x в форме с-таблицы:

Т1	х1	х2	1	bi/ais	bi/ais
e1	-1	-1	15	15	15
e2	5	1	-1	1/5	1
e3	1	-1	5	-	5
e4	0	-1	20	-	20

Т2	e1	x2	1					Т2’	x1	e2	1
х1	-1	-1	15					e1	4	-1	14
e2	-5	-4	74					x2	-5	1	1
e3	-1	-2	20					e3	2	-1	4
e4	0	-1	20					e4	1	-1	19

ОП – получен, следовательно ОП – получен, следовательно

х₂  и e₁ – активные ограничения; x₁ и e₂ – активные ограничения;

из Т₂ получаем:

Т3	e1	e3	1
x1	1	1/2	5
e2	-3	2	34
x2	-1/2	-1/2	10
e4	2	½	10

отсюда делаем вывод, что e₃ – активное ограничение;

из Т₃ получаем:

Т4	e4	e3	1
x1			10
e2			19
x2			15/2
e1			-5

Опорный план не получен, следовательно e₄ – пассивное ограничение.

3.2.Определение p-множества с-методом.

При подготовке решения для ЛПР интерес будет представлять информация обо всем множестве p-оптимальных (эффективных) решений D_x^p. Графический метод позволяет сформулировать довольно простой подход к определению множества D_x^p. Суть этого подхода в следующем. Решая усеченную задачу линейного программирования, устанавливаем факт существования д-конуса ( D_max > 0). Поскольку для линейных ЦФ конфигурация д-конуса не зависит от положения его вершины х^,, то, помещая ее на границу e_i области D_x, решаем усеченную ЗЛП с добавлением e_i, соответствующего i-му участку границ D_x. Вырождение д-конуса в точку х^, будет признаком p-оптимальности и всех других точек данной грани. С помощью с-метода указанная процедура легко проделывается для пространства любой размерности n. Неудобство указанного метода состоит в том, что потребуется на каждой грани ОДР D_x найти точку х^, (по числу граней D_x) сформулировать и решить столько же ЗЛП размера Rxn.

Существенно сократить объем вычислений можно путем выбора вершины д-конуса в фиксированной точке х^, = (1)_n и в нее же параллельно себе перенести грани, составляющие границы D_x

Приведенные к точке х^, = (1)_n приращения d^-r и невязки e_i запишутся в виде:

(8)

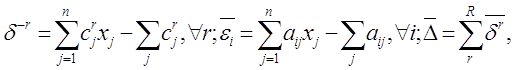
где черта сверху у d, e и D означает, что эти величины приведены к точке х^, = (1)_n.

По существу, (8) – ЗЛП размера (R+m)xn (D®max), а ее решение позволит найти все грани, составляющие p-множество D_x^p.

Составляем с-таблицу, не учитывая пассивные ограничения, т.е e₁:

Т1	х1	х2	1
e2	-1	-1	2
e3	5	1	-6
e4	1	-1	0
х1	1	0	-1
х2	0	1	-1
d1	1	-2	1
d2	1	1	-2
d3	-1	4	-3
D	1	3	-4

В начале решается усеченная ЗЛП (под чертой):

Т2	х1	d1	1
e1	-3/2	1/2	3/2
e2	11/2	-1/2	-11/2
e3	1/2	1/2	-1/2
х1	1	0	-1
х2	1/2	-1/2	-1/2
x2	1/2	-1/2	1/2
d2	3/2	-1/2	-3/2
d3	1	-2	-1
D	5/2	-3/2	-5/2

Т3	d3	d1	1
e1	-3/2	-5/2	0
e2	11/2	21/2	0
e3	1/2	3/2	0
х1	1	2	0
х2	1/2	1/2	0
x2	1/2	1/2	1
d2	3/2	5/2	0
x1	1	2	1
D	5/2	7/2	0

Т4	e1	d1	1
d3			0
x2			1
d2			0
x1			1
D	-5/3	-2/3	0

e₁Î D_x^p, так как D_max = 0.

Данный метод построения множества D_x^p обладает недостатком, связанным с разрушением области допустимых решений (ОДР) D_xпри переносе ее граней в х^,. Действительно, вершины области D_x в преобразованной модели никак не отражены, а именно одна из них может составить p-множество в случае его совпадения с оптимальным решением. Такое совпадение возможно, если все ч-критерии достигают максимум на одной вершине. Физически это значит, что они слабопротиворечивы – угол при вершине д-конуса приближается к 180° (градиенты ч-критериев имеют практически совпадающие направления). Данный случай имеет место, если в p-множество не вошла ни одна из граней ОДР D_x. Следовательно, p-множество совпадает с оптимальным решением. Для определения p-множества решается обычная ЗЛП с одним из ч-критериев. Если при этом получено множество оптимальных решений, то решается ЗЛП с другим ч-критерием. Пересечение оптимальных решений и является p-множеством. Для ЛПР указание на то, что некоторая грань e_i = e_i^p Î D_x^p p-оптимальна, является только обобщенной информацией.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

4.Определение альтернативных вариантов многокритериальной задачи

Наиболее естественным и разумным решением мк-задачи было бы органическое объединение всех ч-критериев в виде единой ЦФ. Иногда это удается сделать путем создания более общей модели, в которой ч-критерии являются аргументами более общей целевой функции, объединяющей в себе все частные цели операции. На практике этого редко удается достигнуть, что, собственно, и является основной причиной появления проблемы многокритериальности. Однако наиболее распространенный подход к решению проблемы пока остается все-таки один: тем или иным путем свести решение мк-задачи к решению однокритериальной задачи. В основе подхода лежит предположение о существовании некой функции полезности, объединяющей в себе ч-критерии, но которую в явном виде, как правило, получить не удается. Получение наиболее обоснованной «свертки» ч-критериев является предметом исследований нового научного направления, возникшего в связи с проблемой многокритериальности - теории полезности. В данной работе будут рассмотрены некоторые подходы, позволяющие получить варианты решения мк-задач при тех или иных посылках и которые лицо принимающее решение (ЛПР) должно рассматривать как альтернативные при принятии окончательного решения и которые, конечно, должны удовлетворять необходимому условию- p-оптимальности.

4.1.Метод гарантированного результата

При любом произвольном решении х Î D_x каждый из ч-критериев примет определенное значение и среди них найдется, по крайней мере, один, значение которого будет наименьшим:

(9)

Метод гарантированного результата (ГР) позволяет найти такое (гарантированное) решение, при котором значение «наименьшего» критерия станет максимальным. Таким образом, целевая функция (ЦФ) является некоторой сверткой ч-критериев (9), а МЗЛП сводится к задаче КВП (кусочно-выпуклого программирования) при ОДР D_x, заданной линейными ограничениями.

Исходные условия записываем в каноническом виде:

d¹ = х₁ - 2х₂ - j + 2,

d² = х₁ + х₂ - j + 4,

d³ = -х₁ + 4х₂ - j + 20,

e₁ = -х₁ - х₂ + 15,

e₂ = 5х₁ + х₂ - 1,

e₃ = x₁ - х₂ + 5,

 потом в виде с-таблицы:

Т1	х1	х2	j	1
e1	-1	-1	0	15
e2	5	1	0	-1
e3	1	-1	0	5
d1	1	-2	-1	2
d2	1	1	-1	4
d3	-1	4	-1	20

Вводя в базис переменную j (d¹ « j), получаем обычную ЗЛП при максимизации ЦФ j.

Т2	х1	х2	d1	1
e1	-1	-1	0	15
e2	5	1	0	-1
e3	1	-1	0	5
j	1	-2	-1	2
d2	0	3	1	2
d3	-2	6	1	18

Т3	d3	x2	d1	1	bi/ais
e1	1/2	-4	-1/2	6	6/4
e2	-5/2	16	5/2	44	-
e3	-1/2	2	2	14	-
j	-1/2	1	-1/2	11	-
d2	0	3	-1	2	-
х1	-1/2	3	1/2	9	-

Т4	d3	e1	d1	1
x2				3/2
e2				68
e3				17
j	-3/8	-1/4	-5/8	25/2
d2				13/2
х1				27/2

Решение ЗЛП приводит к конечной с-таблице Т₄. Видно, что полученное гарантированное решение х p-оптимально, поскольку введение в базис любой свободной переменной (т.е. ее увеличение) приведет к снижению j - нижнего уровня ч-критериев ("с_j < 0). Из таблицы также видно, что решение х⁰=(27/2; 3/2) находится на грани e₄, при этом значения ч-критериев равны (находим по формуле L^r(x^r) = j + d^r):

L₁ = L₃ = j = 25/2

L₂ = j + d₂  = 25/2 + 13/2 = 19

L^S = 88/2 = 44

x° = ( 27/2; 3/2)

Если бы в строке j имелись нули, то это означало бы, что одну из соответствующих переменных можно ввести в базис (увеличить без снижения уровня j). Это могло бы привести и к увеличению приращения d^r для некоторого ч-критерия, находящегося в базисе.

4.2.Метод линейной свертки частных критериев

Линейная свертка ч-критериев получается как х сумма с некоторыми весовыми коэффициентами m_r:

	(9)

где

	(10)

Меняя порядок суммирования и вводя обозначения c_j и c₀, окончательно получим:

	(11)

Коэффициенты веса обычно получаются путем опроса экспертов из соответствующей предметной области. Поскольку вектор m = (m_r) – суть вектор-градиент ЦФ L^m(x), то предполагается, что он указывает направление к экстремуму неизвестной функции полезности. Положительная сторона такого подхода – несложность, не всегда компенсирует его серьезный недостаток – потерю физического смысла линейной свертки разнородных ч-критериев. Это затрудняет интерпретацию результатов, поэтому полученное таким путем решение, следует рассматривать только как возможный (альтернативный) вариант решения ЛПР. Для его сравнительного анализа следует привлекать любые другие варианты и, конечно, значения ч-критериев, получаемые при этом. Иногда при получении свертки ч-критериев предварительно нормируются каким-нибудь способом.

Наиболее приемлемой линейная свертка ч-критериев может оказаться в том случае, когда ч-критерии однородны и имеют единый эквивалент, согласующий их наиболее естественным образом.

На содержательном уровне данная МЗЛП состоит в необходимости принятия такого компромиссного решения (плана выпуска продукции) x^k Î D_x, которое обеспечит, по возможности, наибольшую суммарную выручку L¹(x) от реализации произведенной продукции; наименьший расход ресурсов i-го вида L^pl (x) (i = 1; m); минимальные налоговые отчисления от прибыли L^H(x) (или общей выручки).

Указанные цели носят противоречивый характер, и фактически мы имеем МЗЛП с m+2 –мя ч-критериями (m – количество видов потребляемых ресурсов). ОДР обусловлена ресурсными ограничениями и условиями неотрицательных переменных:

где a_ij – расход ресурса i-го вида для выпуска 1 единицы продукции j-го вида (j=1,n);

 b_i – запас ресурса i-го вида;

e_i – остаток ресурса i-го вида при плане выпуска x = (x_j)_n. Ч-критерии однородны, если они могут быть сведены к единой мере измерения. В качестве такой меры можно взять денежный эквивалент. Тогда m+2 ч-критерия могут быть с помощью линейной свертки сведены к трем:

общая выручка (руб.):

общая экономия ресурсов (руб.):

налоговые отчисления (руб.):

где c_j – выручка от реализации 1 ед. продукции j-го вида (цена); s_i – стоимость (цена) 1 ед. ресурса i-го вида (i = 1;m); П_j – прибыль от реализации 1 ед. продукции j-го вида (j = 1;n); a_j – доля (процент налоговых отчислений от прибыли (выручки).

В заключение заметим, что коэффициенты m_r не обязательно должны удовлетворять условию (10), но обязательно должны быть положительными, если все ч-критерии максимизируются.

Перейдем к решению:

 

Т1	х1	х2	1
e1	-1	-1	15
e2	5	1	-1
e3	1	-1	5
L1	1	-2	2
L2	1	1	4
L3	-1	4	20
LS	1	3	26

Т2	e1	x2	1
x1	-1	-1	15
e2	-5	-4	74
e3	-1	-2	20
L1	-1	-1	17
L2	-1	0	19
L3	1	5	5
LS	-1	2	41

L_1max = 17

L_{2 max} = 19

L₃ = 5

L^S= 41

Т3	e1	L1	1
x1			28/3
e2			154/3
e3			26/3
x2			17/3
L2			19
L3	-2/3	-5/3	100/3
LS	-5/3	-2/3	157/3

5. Составление сводной таблицы.

 

Окончательное решение сводится в таблицу, где записываются альтернативные варианты:

Метод	х0	L1	L2	L3	LS
Метод гарантированного результата	(27/2 ; 3/2)	25/2	19	25/2	44
Метод свертки	(28/3;17/3)	0	19	33 1/3	52 1/3
Оптимизация L1	(15;0)	17	19	5	41
Оптимизация L2, L3	(28/3;17/3)	0	19	33 1/3	52 1/3
xÏDxp	(5;3)	1	12	-13	0