Министерство высшего и профессионального образования
Томский государственный архитектурно-строительный университет
Кафедра Теоретической механики
КУРСОВАЯ РАБОТА по теоретической механике № 1
«Определение угловых скоростей и угловых ускорений звеньев механизма манипулятора по заданному движению рабочей точки»
Вариант № 1
Выполнил:
студент группы 013/12т
Шмидт Дмитрий
Проверил:
Евтюшкин Е.В.
ТОМСК – 2004
Решение.

![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()


 |
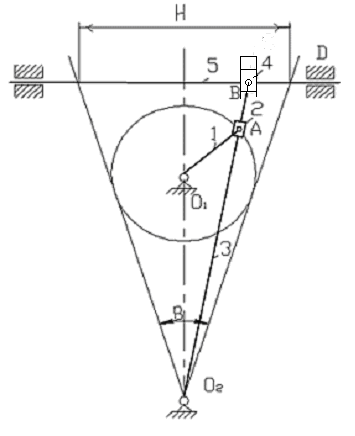
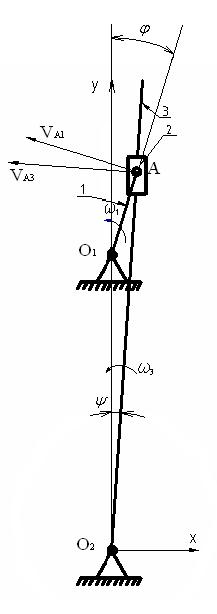
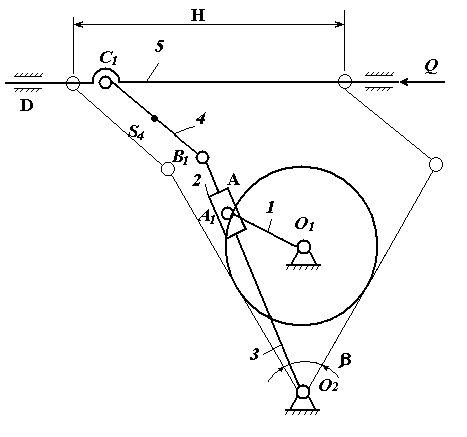
а=0,5 м; b=1,2 м; c=0,4 м; ХА=1,4091 м; (1)
φ0=600; ψ0=150; YА=0,7436-0,1 *t м;
XA=0; XA=0;
YA=-0,1; YA=0.
Уравнения связей:
|OA|=|OD|+|DA| (2) |OD|=a=const; |DA|=b=const;
|DC|=|DB|+|BC| (3) |DC|=c=const;|BC|=c=const;
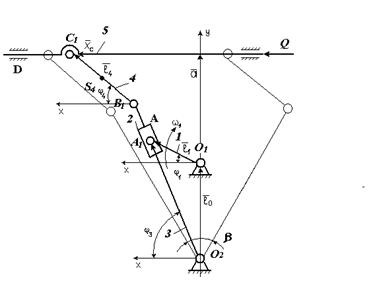
Проекции (2) на оси координат:
XA=a*cos φ+b*cos ψ; (4)
YA=a*sin φ-b*sin ψ;
После дифференцирования (4) по t имеем:
a*sin φ*φ+b*sin ψ*ψ=0; (4)’
-a*cos φ*φ-b*cos ψ*ψ=0.1;
Решения (4)’ в общем виде:
φi=0,1*sin ψ i/a*sin (φi- ψ i); (4.1)’
ψi=-0,1*sin φi/b*sin (φi-ψi); (4.2)’
(4.1)’ и (4.2)’ с учетом заданных параметров:
φi=0,2*sin ψi/sin(φi-ψi); [1]
ψi=-0,0833*sin φi/ sin (φi-ψi); [2]
После дифференцирования по t (4)’ имеет вид:
a*sin φ*φ+b*sin ψ*ψ=-(a*φ2*cosφ -b*ψ2*cos ψ); (4)”
-a*cos φ*φ-b*cos ψ*ψ=-(a*φ2*sin φ+b*ψ2*sin ψ);
Решения (4)” в общем виде:
φi= -[(a*φi2*cos (φi-ψi)+b*ψi2)/a*sin(φi-ψi)]; (4.1)”
ψi= (b* ψi2*cos (φi-ψi)+a*φi2)/b*sin(φi-ψi)]; (4.2)”
(4.1)” и (4.2)” с учетом заданных параметров:
φi=-[( φi2*cos (φi-ψi)+2.4*ψi2)/ sin(φi-ψi)];] [3]
ψi= (ψi2*cos (φi-ψi)+0.4167*φi2)/sin (φi-ψi); [4]
Проекции [3] на оси координат:
c*cos ψ =c*cos θ +S*cos φ; (5)
c*sin ψ =-c*sin θ +S*sin φ;
Находим параметры S и θ для t=0:
(-c*cos θ0) 2=(-c*cos ψ 0+S0*cos φ0) 2;
(c*sin θ0) 2=(-c*sin ψ 0+S0*sin φ0) 2;
c2=c2-2*c*S0*cos (φ0-ψ0)+S02, отсюда S0=2*c* cos (φ0-ψ0)=0.5657м;
Разделив первое уравнение (5) на второе, имеем:
- сtg θ0=(-c*cos ψ 0+S0*cos φ 0)/ -c*sin ψ 0+S0*sin φ 0=(-0.4*0.965+0.5657)/-0.4*0.2588+0.5657*0.866=-0.2668
Тогда θ0=75.00.4’
После дифференцирования (5) по t имеем:
c*sin θ*θ-cos φ *S=c*ψ*sin ψ -S*φ*sin φ; (5)’
c*сos θ*θ-sin φ *S=-c*ψ*cosψ +S*φ*cos φ;
Решения (5)’ в общем виде:
θi=(-c*ψi*cos (φi-ψi)+Si* φ i)/c*cos (θi+ φ i); (5.1)’
Si=S*φi*sin (θi+φi)-ci*ψi*sin (θi+φi)/cos (θi+ φ i); (5.2)’
(5.1)’ и (5.2)’ с учетом заданных параметров:
θi=-ψ i*cos (φi-ψi)+2.5*Si* φ i/cos (θi+ψi); [5]
Si=S*φi*sin (θi+φi)-0.4*ψi*sin (θi+ψi)/cos (θi+ φ i); [6]
После дифференцирования (5)’по t имеем:
с*sin θ*θ-cos φ *S=-2S*φ*sin φ-S(φ*sin φ+ φ2cos φ)+c(ψ*sin ψ+ ψ2 *cos ψ)-с*θ2*cos θ (5)”
с*cos θ*θ-sin φ *S=2S*φ*cos φ+S(φ*cos φ- φ2sin φ)- c(ψ*cos ψ- ψ2 *sin ψ)-с*θ2*sinθ
Решения (5)” в общем виде:
θi=[2S*φ+S* φ-c[ ψ*cos(φ-ψ)+ ψ2*sin(φ- ψ)]+c* θi2 *sin (φ +θ)]/c*cos(θ+φ) (5.1)”
Si= 2S*φ*sin (θ+φ) +S*[ φ *sin(φ+θ)+ φ 2*cos(φ+θ)]-c*[ ψi *sin (ψ +θ)+ ψ2cos(θ+ψ)]+с * θi2/c*cos(θ+φ) (5.2)”
(5.1)” и (5.2)” с учетом заданных параметров:
θi=[2,5*(2*S* φ+S φ)-[ ψ cos (φ-ψ)+ φ2sin(φ-ψ)]+ θi2*sin(θ+φ)]/ cos (θ+φ); [7]
Si=[2*S* φsin(θ+φ)+S[φsin(θ+φ)+ φ2 cos (θ+φ)]-0.4[ψ sin(φ+ ψ)+ ψ2*cos(θ+ ψ)+ θi2]/ cos (θ+φ); [8]
Используя формулы [1]÷[8] вычисляем текущие параметры, а с помощью формул [9] находим последующие параметры:
φi+1=φi+φi*∆t+φi*∆t2/2; φi+1=φi+0,2*φi+0,02*φi;
ψi+1=ψi+ψi*∆t+ψi*∆t2/2; ψi+1=ψi+0,2*ψi+0,02*ψi; [9]
θi+1=θi+θi*∆t+θi*∆t2/2; θi+1=θi+0,2*θi+0,02*θi;
Si+1=Si+Si*∆t+Si*∆t2/2; Si+1=Si+0,2*Si+0,02*Si;
где ∆t=0,2 c.
Полученные результаты заносим в сводную таблицу.
| t, c | φ | ψ | θ | S | ||||||||
| φ, рад | φ, с-1 | φ, с-2 | ψ, рад | ψ, с-1 | ψ, с-2 | θ, рад | θ, с-1 | θ, с-2 | S, м | S, м*с-1 | S, м*с-2 | |
| 0 | 1,0440 | 0,0732 | -0,0479 | 0,2610 | -0,1020 | -0,0281 | 1,3061 | -0,2480 | 0,1233 | 0,5657 | -0,0988 | 0,0947 |
| 0,2 | 1,0577 | 0,0654 | -0,0363 | 0,2411 | -0,0995 | -0,0115 | 1,2589 | -0,2318 | 0,0833 | 0,5478 | -0,0970 | 0,0758 |
| 0,4 | 1,0700 | 0,2214 | 1,2136 | 0,5299 | ||||||||
Параметры для t=0,4;0,6;0,8;1,0 (с) находим по алгоритму для t=0 и t=0,2 (c), приведенному ниже.
t=0: sin ψ0=0,2588; sin φ0=0,866; sin (φ0-ψ0)=0,7071;
cos (φ0-ψ0)=0,7071;
[1] φ0=0,2*0,2588/0,7071=0,0732; φ02=0,0053;
[2] ψ0=-[0,0833*0,866/0,7071]=-0,1020; ψ02=0,0104;
[3] φ0=-[2,4*0,0104+0,0053*0,7071/0,7071]=-0,0479;
[4] ψ0=0,4167*0,0053+0,01040*0,7071/0,7071=0,0281;
[9] φ1=1,0440+0,0146-0,0009=1,0577 (60037’); φ1-ψ1=46049’
ψ1=0,2610-0,0204+0,005=0,2411 (13048’); sin (φ1-ψ1)=0,7292;
cos (φ1-ψ1)=0,6843;
θ02=0,0615;
θ0+φ0=135004’: sin (θ0+φ0)=0,7062;
cos (θ0+φ0)=-0,7079;
θ0+φ0=90004’: sin (θ0+ ψ 0)=1.0;
cos (θ0+ ψ 0)=-0,0012;
[5] θ0=-0,1290*0,5736-1,25*0,9178*0,2034/0,0.7079=-2480;
[6] S0=-0,8*0,1290*0,9397-0,9178*0,2034*0,7660/0,7079=-0,0988;
[7] θ0=-0,0496*0,5736-0,0266*0,8192-2,5*0,0802*0,2034-1,25*0,9178*0,0559+0,0772*
*0,8192/0,7079=0,1233;
[8] S0=-0,8*(-0,0496*0,9397-0,0166*0,3420+0,0772)-2*0,0802*0,8192*0,2034+0,9178*
*(-0,0559*0,8192-0,0414*0,5736)/0,7079=0,0947;
[9] θ1=1,3061-0,0496+0,0024=1,2589 (72010’);
S1=0,5657-0,0197+0,0018=0,5478м;
θ1+ψ1=85058’; θ1+φ1=132047’;
sin (θ1+ψ1)=0,9976; sin (θ1+φ1)=0,7339;
cos (θ1+ψ1)=0,0704; cos (θ1+φ1)=-0,6792;
t=0,2 c: sin ψ1=0,2386; sin φ1=0,8714; sin (φ1-ψ1)=0,7292;
cos (φ1-ψ1)=0,6843;
[1] φ1=0,25*0,3832/0,8076=0,0654; φ12=0,0042;
[2] ψ1=-0,3333*0,52/0,8076=-0,0995; ψ12=0,099;
[3] φ1=-0,0141*0,5896+0,75*0,0461/0,8076=-0,0363;
[4] ψ1=-0,0461*0,5896+1,3333*0,0141/0,8076=0,0115;
[9] φ2=1,0577+0,0130-0,0007=1,0700 (61020’); φ2-ψ2=48039’;
ψ2=0,3932-0,0429-0,0011=0,2214(12041’);
S1=0,5478 м; sin (θ+ψ1)=0,9976; sin (θ+φ1)=0,7339;
cos (θ1+ψ-1)=0,0704; cos (θ1+φ1)=-0,6792;
[5] θ1=0,1186*0,5896+1,25*0,9363*(-0,2146)/-0,6792=-0,2318; θ12=0,0537;
[6] S1=0,8*0,1186*0,9508-0,9363*0,2146*0,7118/-0,6792=-0,0970;
[7] θ1=-0,0531*0,5896-0,0146*0,8076-2,5*0,0902*0,2146-1,25*0,9363*0,057+0,096*
*0,8109/-0,6792=0,0833;
[8] S1=-0,8*(-0,0531*0,9508-0,0141*0,3098+0,0960)-2*0,0902*0,2146*0,8109+0,9363*
*(-0,057*0,8109-0,0461*0,5852)/-0,6792=0,0758;
[9] θ2=1,2589-0,0463+0,0016=1,2136 (69033’);
S2=0,5478-0,0194+0,0015=0,5299 м;
θ2+ψ2=127001’; θ2+φ2=157042’;
sin (θ2+ψ2)=0,6533; sin (θ2+φ2)=0,1684;
cos (θ2+ψ2)=-0,1568; cos (θ2+φ2)=-0,3875;
Похожие работы
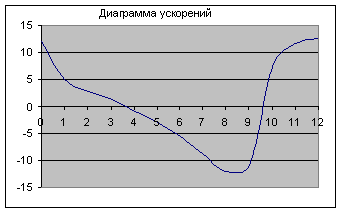
... 7,41 11,96 12,6 Графические 2,5 ; Диаграммы скоростей и ускорений: Рис.4 - Диаграмма скоростей Рис.5 - Диаграмма ускорений 2. Силовой анализ рычажного механизма Исходные данные: Масса кулисы m3=20 кг; Масса ползуна m5=52 кг; Сила полезного сопротивления Qпс=1550 Н. Схема механизма (Рис.6). ...
... 7,5 7,5 аА’ 3,8 2,5 2,6 6,4 8,5 10,3 7,5 ab 5,7 3,4 3,8 10,5 19,3 21,4 11 ac 5,8 2,1 1,7 10,5 16,1 20,8 11,7 1.5 Диаграммы движения выходного звена. Диаграмму перемещения строим , используя полученную из S-t плана механизма траекторию движения точки С. Диаграммы скорости V-t и ускорений A-t строим из полученных 12 планов скоростей ...
... к точности, хотя это уменьшение весьма не значительное. 4.Программные средства для исследования динамической модели портального манипулятора 4.1 Программа для вычисления параметров переходного процесса портального манипулятора Для исследования полученной динамической модели, построения графиков приведенных в работе, использовалась программа “Модель портального манипулятора МРЛ-901П в момент ...
... уменьшение времени перемещения, что можно использовать на операциях с низким требованием к точности, хотя это уменьшение весьма не значительное. 4. Программные средства для исследования динамической модели портального манипулятора 4.1 Программа для вычисления параметров переходного процесса портального манипулятора Для исследования полученной динамической модели, построения графиков приведенных в ...


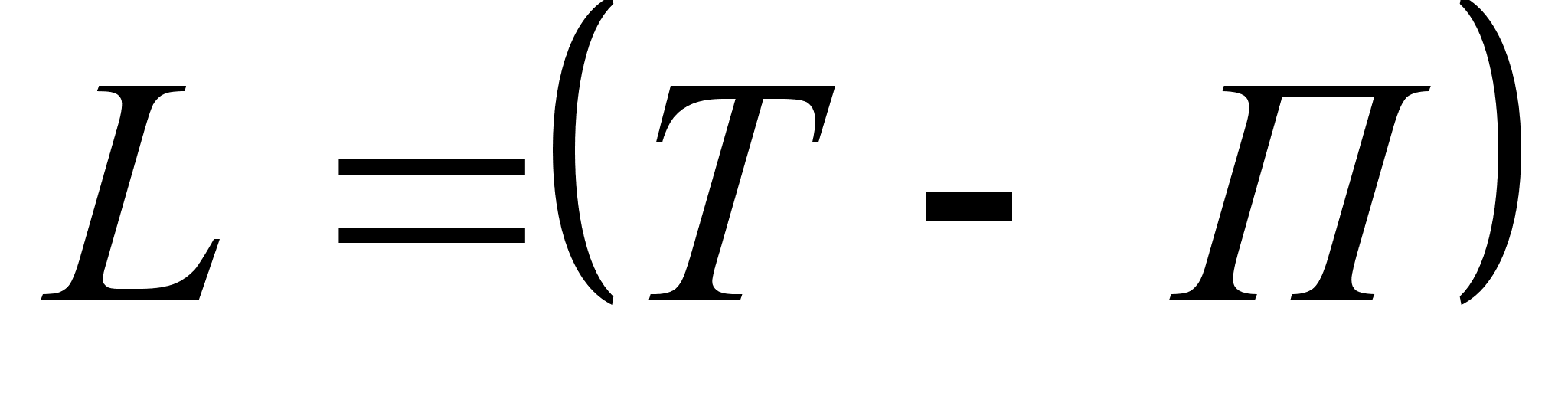

0 комментариев