Навигация
Синтез и анализ рычажного механизма
Содержание
Введение
1. Синтез и анализ рычажного механизма
1.1 Структурный анализ механизма
1.2 Определение скоростей
1.3 Значения скоростей из плана скоростей
1.4 Определение ускорений
1.5 Диаграммы движения выходного звена
1.6 Определение угловых скоростей и ускорений
1.7 Скорости и ускорения центров масс
1.8 Аналитический метод расчёта
1.8.1 Расчёт скоростей и ускорений на ЭВМ
2. Силовой анализ рычажного механизма
2.1 Силы тяжести и силы инерции
2.2 Расчёт диады 4-5
2.3 Расчёт диады 2-3
2.4 Расчёт кривошипа
2.5 Рычаг Жуковского
2.6 Определение мощностей
2.7 Определение кинетической энергии механизма
2.7.1 Расчёт сил инерции на ЭВМ
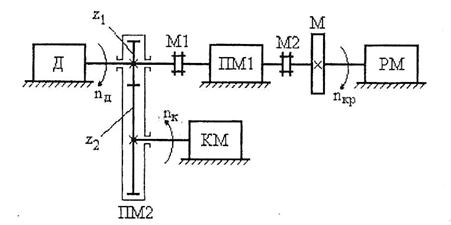
3. Проектирование зубчатого зацепления. Синтез планетарного редуктора
3.1 Геометрический расчет равносмещенного зубчатого зацепления
3.2 Синтез планетарного редуктора
3.3 Определение частот вращения аналитическим методом
4. Синтез и анализ кулачкового механизма
4.1 Диаграмма движения толкателя
4.2 Масштабный коэффициент времени
4.3 Масштабный коэффициент ускорения
4.4 Максимальные значения скорости, ускорения толкателя
Список использованных источников
Введение
В механизмах привода поперечно строгальных станков используется механизм, обеспечивающий главное возвратно-поступательное движение резания. Основная масса механизмов использующихся в данных станках это кулисные механизмы. Они обеспечивают заданную скорость рабочего хода и повышенную скорость холостого хода. Расчёт и проектирование данных механизмов является важным этапом в образовании инженера.
В курсе предмета "Теория машин, механизмов и манипуляторов" получаются навыки расчёта механизмов машин. Комплексным подходом к закреплению полученных знаний является выполнение курсового проекта по данному курсу. В курсовом проекте осуществляется синтез и расчёт кулисного механизма, построение и расчёт зубчатого зацепления и кулачкового механизма. При выполнении работы используются все знания, полученные за курс предмета.
1. Синтез и анализ рычажного механизма
Исходные данные:
Ход ползуна: Н= 430 мм;
Коэффициент производительности: К=1,46;
Межосевое расстояние: О1О2 = 320 мм;
Сила полезного сопротивления: Qпс = 1550 Н;
Частота вращения кривошипа: nкр= 100 мин - 1;
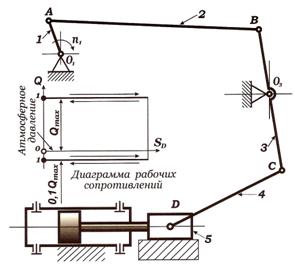
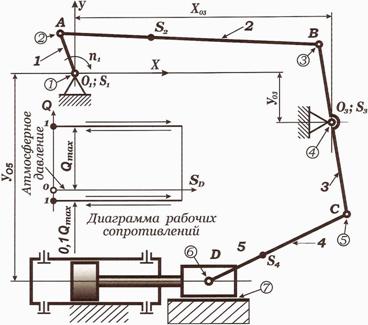
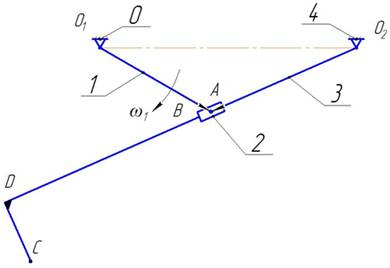
Схема механизма (Рис.1).
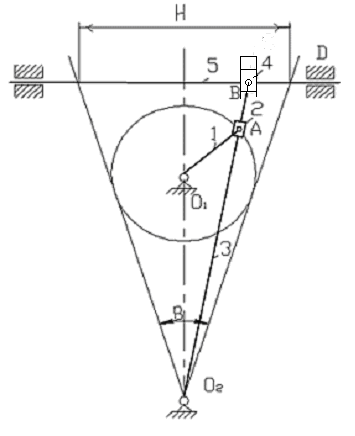
Рис.1 - Схема механизма
1.1 Структурный анализ механизмаМеханизм состоит из пяти звеньев: кривошипа - 1, камней- 2,4, кулисы - 3, и ползуна - 5.
Звенья образуют семь кинематических пар: четыре вращательных (А, С, О1, О2), три поступательных (А|, С|, В).
Степень подвижности механизма:
![]()
где n - число подвижных звеньев, n = 5;
р1 - число одноподвижных кинематических пар, р1 = 7;
р2 - число двуподвижных кинематических пар, р2 = 0.
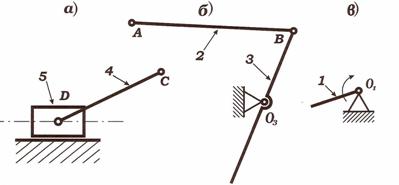
Разложение механизма на структурные группы Ассура:
![]()
![]()
![]()
![]()
![]()
![]() D 5 B, B’
D 5 B, B’
![]()
![]()
![]()
![]()
![]()
![]()
4
II2(4,5) – группа Ассура 2 – го класса, 2 – го порядка, W=0.
![]()
![]() 2
2
A A’
![]()
![]() O2 3
O2 3
![]()
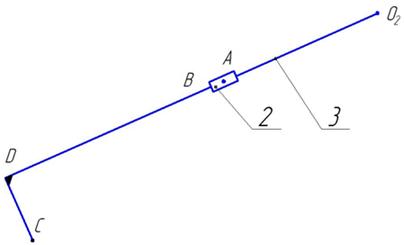
II2(2,3) – группа Ассура 2 – го класса, 2 – го порядка, W=0.
![]()
![]() 1
1
w
![]() O1
O1
![]()
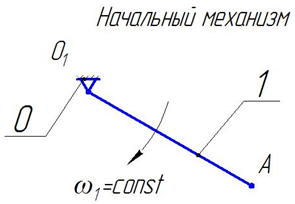
I (0,1) - механизм 1 - го класса, W=1.
Формула строения механизма: I (0,1) →II2 (3,4) →II2 (4,5).
Механизм 2 - го класса, 2 - го порядка.
Определение недостающих размеров механизма
Неизвестные размеры кривошипа и кулисы определяем в крайних положениях механизма. Крайними положениями являются положения, в которых кулиса касается кривошипной окружности.
Угол размаха кулисы:
![]() .
.
Длина кривошипа:
![]()
Длина кулисы:
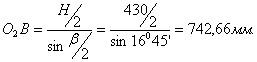
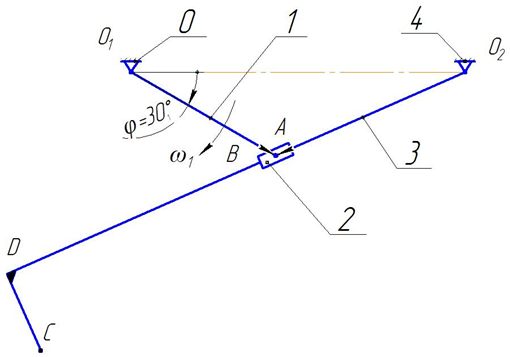
Строим план механизма в 3-м положении, приняв за начало отсчёта крайнее положение, соответствующее началу рабочего хода механизма.
Масштабный коэффициент длин Кl:
![]()
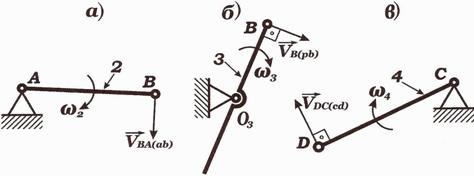
1.2 Определение скоростей
Расчёт скоростей выполняется для третьего положения.
Частота вращения кривошипа: nкр = 100 мин-1.
Угловая скорость кривошипа:
![]()
где ω1 - угловая скорость кривошипа, рад/с.
Скорость точки А:
![]()
Масштабный коэффициент скоростей:
![]()
Из системы векторных уравнений определяем скорость точки ![]() :
:

![]()
![]()
Скорость точки кулисы В| определяем по свойству подобия:
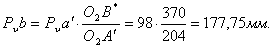
![]()
Из системы векторных уравнений определяем скорость точки В:
![]()
Значения скоростей из плана скоростей
![]() ,
, ![]()
Расчёт ускорений выполняется для третьего положения.
Ускорение точки А кривошипа:
![]()
Масштабный коэффициент ускорений:
![]()
Пересчётный коэффициент:
![]()
Из системы векторных уравнений определяем ускорение точки ![]() кулисы:
кулисы:

Расчёт кориолисового и нормального ускорений:

Вектора кориолисового и нормального ускорений на плане ускорений:
![]()
![]()
Значения ускорений точки ![]() на плане ускорений:
на плане ускорений:
![]()
![]()
Ускорение точки кулисы В определяем по свойству подобия:
![]()
![]()
Система уравнений ускорения точки В, соединяющей 4 и 5 звено:

Определяем кориолисово ускорение:
![]()
Вектор кориолисового ускорения на плане ускорений:
![]()
Значение ускорения точки В на плане ускорений:
![]()
Диаграмма перемещения S-t строится, используя полученную из плана механизма траекторию движения точки В.
Масштабные коэффициенты диаграмм:
![]()
![]()
![]()
![]()
![]()
Угловые скорости и ускорения звеньев механизма определяем в 3-ем положении.
Угловые скорости:
![]()
Угловые ускорения:
![]()
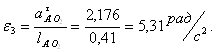
Относительные угловые скорости:
![]()
![]()
![]()
1.7 Скорости и ускорения центров масс
![]()
![]()
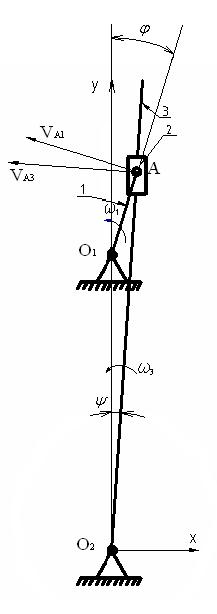
Рис. 2 – Расчётная схема механизма
1.8 Аналитический метод расчёта
Кулисный механизм состоит из звеньев: кривошипа 1, кулисного камня 2, кулисы 3 и стойки.
Положение точки А определяется уравнениями:
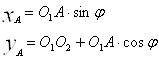
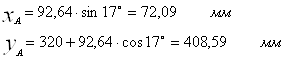
Угол размаха кулисы можно определить по уравнению:
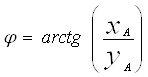
![]()
Скорость точки А1, принадлежащей кривошипу 1 равна:
![]()
![]()
Скорость точки А3, принадлежащей кривошипу 3 равна:
![]()
![]()
Расстояние AB:
![]() (5)
(5)
![]()
Угловая скорость кулисы:
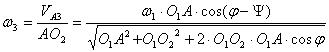
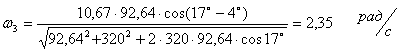
Продифференцируем уравнение (6) по времени:
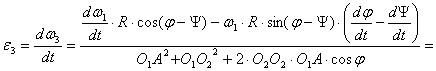

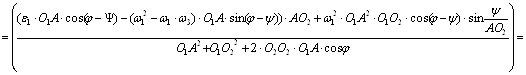
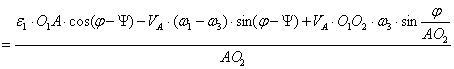

Рис.3 – Расчетная схема кулисного механизма

Положение точки А ползуна:
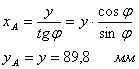
![]()
Ход ползуна из первого крайнего положения:
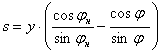 ,
, 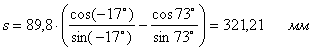
Дифференцируем:
![]()
Дифференцируем:
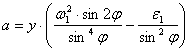 ;
; 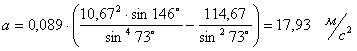
Kulis ()
Const H = 0.430
Const L0 = 0.16
Const L1 =0.092
Const a = 0.27
Const Wl = 10,67
i = 2
For fl = 18 * 3.14/180 To 378 * 3.14 /180 Step 30 * 3.14 /180
Cosf3 = L1 * cos (fl) / ( ( (LI ^ 2 + L0 * LI * sin (fl)) ^ (1/2))
U31 = (cosf3 ^ 2) * (LI ^ 2 + L0 * LI * sin (fl)) / (LI ^ 2 * (cos (fl) ^ 2))
T = (LI ^ 2) + L0 * LI * sin (fl)
Q = (LI ^ 2) + (L0 ^ 2) + 2 * L0 * LI * sin (fl)
w3 = Wl * (T / Q)
up31= (L0*LI*cos (fl) * (L0^2 - LI^2)) / ( ( (L0^2) - (LI^2) + 2*L0*LI*sin (fl)) ^2)
e3= (Wl ^2) *up31
sinf3 = (L0 + LI * sin (fl)) / ( (LO ^ 2 + LI ^ 2 +2*LO*L1 * sin (fl)) ^ (1/2))
u53= (a/ (sinf3^2))
vb = w3 * u53
Worksheets (1). Cells (3, I + 1). Value = CDbl (Format (vb, "Fixed"))
Up53 = (2 *a * cosf3) / (sinf3 ^ 3)
Ab = (w3 ^ 2) * up53 + e3 * u53
Worksheets (l). Cells (8,1 + 1). Value = CDbl (Forrnat (ab, "Fixed"))
Worksheets (l). Cells (2, i). Value - 1 - 2
Worksheets (l). Cells (7, i). Value = 1-2
I = I + 1
Next fl
Worksheets (l). Cells (2, l). Value = "Vb, м/c"
Worksheets (l). Cells (3,1). Value = "Аналитические"
Worksheets (l). Cells (4,1). Value = "Графические"
Worksheets (l). Cells (7, l). Value = "ab, м/c"
Worksheets (l). Cells (8,1). Value = " Аналитические "
Worksheets (l). Cells (9, l). Value = "Графические"
Worksheets (l). Cells (l,
1). Value = "Taблица1"
Worksheets (l). Cells (l,
5). Value - "Значения скоростей Vb, м/с"
Worksheets (l). Cells (6, l). Value = "Taблица 2"
Worksheets (l). Cells (6,5). Value = "Значения ускорений ab, м/с2"
End Sub
Таблица 1.3 - Значения скоростей
| Скорости | Величина скорости, м/с | ||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Расчётные | 0 | 0,79 | 1,29 | 1,73 | 1,7 | 1,23 | 0,81 | 0,09 | -0,96 | -2,29 | -2,35 | -1,29 | 0 |
| Графические | 1,75 | ||||||||||||
Таблица 1.4 - Значения ускорений
| Ускорения | Величина ускорения, м/с^2 | ||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | |
| Расчётные | 12,06 | 5,06 | 2,91 | 2,47 | -0,83 | -2,79 | -5,49 | -8,7 | -12,12 | -10,83 | 7,41 | 11,96 | 12,6 |
| Графические | 2,5 | ||||||||||||
![]() ;
; ![]()
Диаграммы скоростей и ускорений:
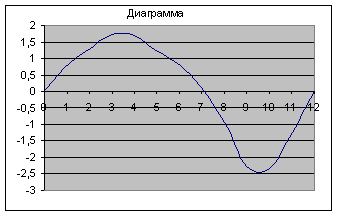
Рис.4 - Диаграмма скоростей
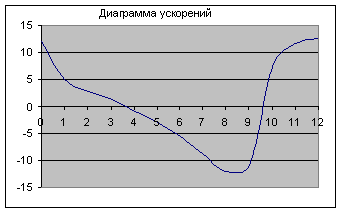
Рис.5 - Диаграмма ускорений
2. Силовой анализ рычажного механизма
Исходные данные:
Масса кулисы m3=20 кг;
Масса ползуна m5=52 кг;
Сила полезного сопротивления Qпс=1550 Н.
Схема механизма (Рис.6).
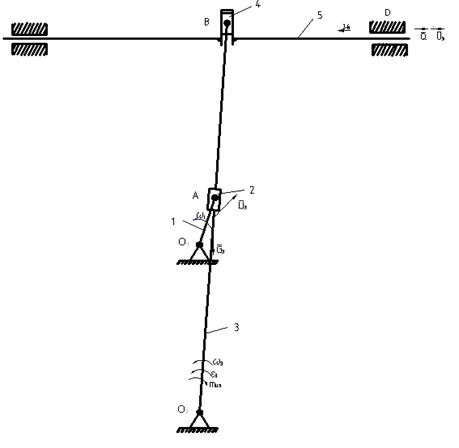
Рис.6 - Расчётная схема механизма
2.1 Силы тяжести и силы инерцииСилы тяжести:
![]()
![]()
Силы инерции:
![]()
![]()
Выделяем из механизма диаду 4,5. Нагружаем её силами Q, U5, G5 и реакциями R50, R43.
Под действием этих сил диада 4,5 находится в равновесии.
Уравнение равновесия диады 4,5:
![]() ;
; ![]()
Анализ уравнения:
Q=1550H;
U5=130H;
G5=510,12Н.
Уравнение содержит две неизвестные, поэтому графически оно решается.
Выбираем масштабный коэффициент сил:
![]()
Вектора сил на плане сил:
![]()
![]()
Значение сил на плане сил:
![]()
![]()
![]()
![]()
![]() ;
; ![]()
Выделяем из механизма диаду 2,3. Нагружаем её силами G3, U3 и реакциями R34 = - R43, R21, R30.
Под действием этих сил диада 2,3 находится в равновесии.
Уравнение равновесия диады 2,3:
![]()
Анализ уравнения:
G3 = 196,2 H;
U3 = 25 H;
R34 = 1680 Н.
Уравнение содержит три неизвестные, поэтому составляем дополнительно уравнение моментов сил относительно точки O2 и находим силу R21:
![]()
![]()
Выбираем масштабный коэффициент сил:
![]()
Вектора сил на плане сил:
![]() ,
, ![]()
Значение силы на плане сил:
![]()
![]()
![]()
![]() ;
; ![]()
Уравнение равновесия кривошипа
![]()
![]()
Реакция R12 известна и равна по величине, но противоположна по направлению реакции R21.
Уравнение имеет 2 неизвестные.
Выбираем масштабный коэффициент сил:
![]()
Значения сил на плане сил:
![]()
![]()
Строим повёрнутый на 900 план скоростей, прикладываем к нему все внешние силы, действующие на механизм.
Уравнение моментов относительно полюса Pv и определяем Pу:
![]()
![]()
![]()
Погрешность расчёта силы Ру:
![]()
Потери мощности в кинематических парах:
![]()
Потери мощности на трение во вращательных парах:
![]()
где ![]() - коэффициент
- коэффициент
![]() - реакция во вращательной паре,
- реакция во вращательной паре,
![]() - радиус цапф.
- радиус цапф.

Суммарная мощность трения
![]()
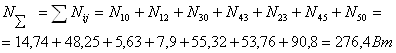
Мгновенно потребляемая мощность
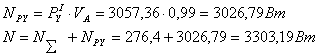
Мощность привода, затрачиваемая на преодоление полезной нагрузки.
![]()
Кинетическая энергия механизма равна сумме кинетических энергий входящих в н![]() его массивных звеньев.
его массивных звеньев.
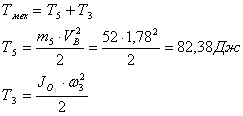

Приведенный момент инерции
![]()
![]()
Sub Kulis 2 ()
Const H = 0.430
Const L0 = 0.16
Const L1 =0.092
Const a = 0.27
Const m = 0.27
Const Wl = 10,67
i = 2
For fl = 18 * 3.14/180 To 378 * 3.14 /180 Step 30 * 3.14 /180
Cosf3 = L1 * cos (fl) / ( ( (LI ^ 2 + L0 * LI * sin (fl)) ^ (1/2))
U31 = (cosf3 ^ 2) * (LI ^ 2 + L0 * LI * sin (fl)) / (LI ^ 2 * (cos (fl) ^ 2))
T = (LI ^ 2) + L0 * LI * sin (fl)
Q = (LI ^ 2) + (L0 ^ 2) + 2 * L0 * LI * sin (fl)
w3 = Wl * (T / Q)
up31= (L0*LI*cos (fl) * (L0^2 - LI^2)) / ( ( (L0^2) - (LI^2) + 2*L0*LI*sin (fl)) ^2)
e3= (Wl ^2) *up31
sinf3 = (L0 + LI * sin (fl)) / ( (LO ^ 2 + LI ^ 2 +2*LO*L1 * sin (fl)) ^ (1/2))
Up53 = (2 *a * cosf3) / (sinf3 ^ 3)
Ab = (w3 ^ 2) * up53 + e3 * u53
Ub = (Ab * m) /2
Worksheets (l). Cells (8,1 + 1). Value = CDbl (Format (Ub, "Fixed"))
Worksheets (l). Cells (2, i). Value - 1 - 2
I = I + 1
Next fl
Worksheets (l). Cells (2, l). Value = "Ub, H"
Worksheets (l). Cells (l,
1). Value = "Taблица1"
Worksheets (l). Cells (l,
5). Value - "Значения сил инерции Ub, м/с"
End Sub
Таблица 1.5 - Значение сил инерции кулисы 3.
| Величина силы инерции, Н | ||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 120, б | 50,6 | 29,1 | 24,7 | -8,3 | -27,9 | -54,9 | -87 | -121,2 | -108,3 | 74,1 | 119,6 | 126 |
Таблица 1.6 - Значение сил инерции кривошипа 5.
| Величина силы инерции, Н | ||||||||||||
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 606 | 188,1 | 82,9 | 81,3 | -18,3 | -129,4 | -281 | -514,1 | -560,1 | -436,9 | 254,8 | 607,7 | 606 |
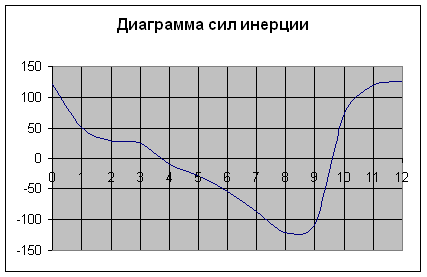
Рис.6 - Диаграмма сил инерции кулисы 3.
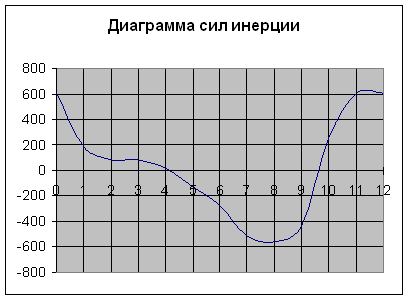
Рис.7 - Диаграмма сил инерции ползуна 5.
3. Проектирование зубчатого зацепления. Синтез планетарного редуктора 3.1 Геометрический расчет равносмещенного зубчатого зацепления
Исходные данные:
Число зубьев на шестерне ![]()
Число зубьев на колесе ![]()
Модуль ![]()
Угол профиля рейки ![]()
Коэффициент высоты головки зуба ![]()
Коэффициент радиального зазора ![]()
Суммарное число зубьев колес ![]()
Поскольку ![]() , то проектируем равносмещенное зубчатое зацепление. Коэффициент смещение
, то проектируем равносмещенное зубчатое зацепление. Коэффициент смещение
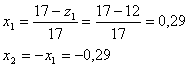
Угол зацепления ![]()
Делительное межосевое расстояние
![]()
Начальное межосевое расстояние: ![]()
Высота зуба: ![]()
Высота головки зуба
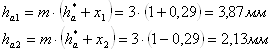
Высота ножки зуба
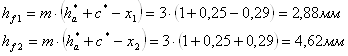
Делительный диаметр
![]()
Осевой диаметр
![]()
Диаметр вершин
![]()
Диаметр впадин
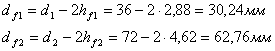
Толщина зуба по делительному диаметру
![]()
Делительный шаг: ![]()
Шаг по основной окружности: ![]()
Радиус галтели: ![]()
Коэффициент перекрытия:
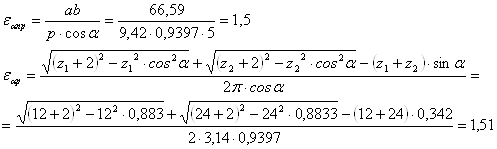
Погрешность определения коэффициента зацепления:
![]()
где ab и p находим из чертежа картины зацепления.
Похожие работы
... этого отрезка в миллиметрах вычислим момент инерции маховика. Углы вычисляем по формулам: Проводим вычисления и находим: Проводим касательные и измеряем длину отрезка KL. 3. Динамический анализ рычажного механизма 3.1 Построение планов скоростей и ускорений в заданном положении Вычертим кинематическую схему механизма в заданном положении градусов. При построении ...
... ,5 – 174,5 90 Δ, % 0,00 0,00 0,00 0,00 0,00 0,00 0,00 ПРИВЕДЁННЫЕ ФАКТОРЫ Положение 2 Расчёт ЭВМ Погрешность Δ, % – 156,6 – 156,6 0,00 IПР 0,22 0,22 0,00 2. Синтез и анализ кулачкового механизма 2.1 Построение диаграмм движения толкателя 1. Строится заданная диаграмма ускорений толкателя. Максимальная ордината ...
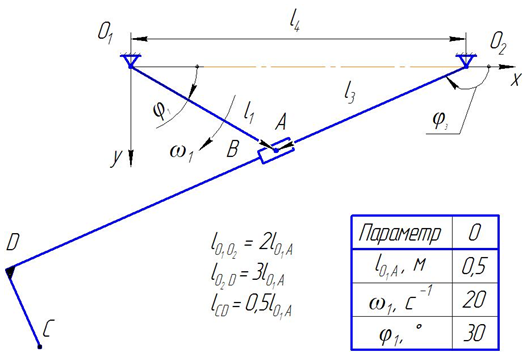
... [lCD]: Методом засечек в принятом масштабе µ строим план положения механизма для заданного положения кривошипа О1А, φ1 = 30° (рис. 5). Рис. 5 План положения механизма, µ = 0,01 м/мм 3. Кинематический анализ рычажного механизма Построение плана скоростей. План скоростей строим для заданного положения механизма, для φ1 = 30° (рис. 5). Построение плана скоростей начинаем ...
... 2.7 Определение кинетической энергии и приведенного момента инерции механизма Кинетическая энергия механизма равна сумме кинетической энергии звеньев: Тмех=∑Тi Для механизма насоса с заданными параметрами кинетическая энергия звена равна: ∑Тi=Т3+Т5= Где JO2’==12·0,352/3=0,49 кг·м2 JO2’’==30·0,1552/3=0,24 кг·м2 Т3=(0,49+0,24)·4,942/2=8,9 ...
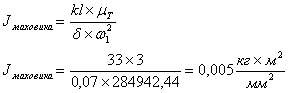
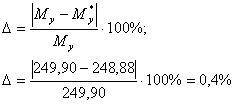
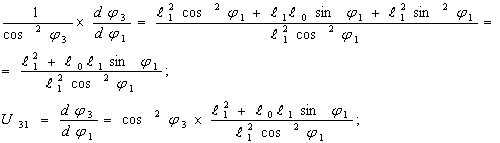
0 комментариев