Навигация
Расчет показателя качества системы
4. Расчет показателя качества системы
Показателем качества данной системы является колличесво земных станций, ретранслируемых в одном стволе БРТР (N).
В общем случае N=Dfствола/Dfстанции, где
--Dfствола -- полоса частот, отведенная для одного ствола. дfствола=70 МГц (см.ТЗ.)
-- Dfстанции -- ширина спектра сигнала одной ЗС, ретранслируемой в данном стволе. Dfстанции=Dfс*Nк, (Nк=50 -- число телефонных каналов на одной ЗС (см.ТЗ.), дfс -- ширина спектра сигналов одного канала). Т.к. Dfс=R/log M (где R=64 кбит/с), то Dfстанции=Nк* *(R/log M)=64000*50/log M.(здесь,ранее и далее log имеет основание 2, исключая случаи, где оно не оговорено отдельно).
Далее приведена таблица расчета значений N в зависимости от различных М :
| Кратность ФМ-сигнала | Dfстанции, кГц | N |
| 2 | 3200 | 21.875 |
| 4 | 1600 | 43.75 |
| 8 | 1066.667 | 65.625 |
В стремлении достичь максимума показателя качества N, естественно выбрать сигнал ФМн с М=8 (N=65).
5. О построении ФМ и АФМ сигналов.
В основу принципов построения ФМ сигналов заложено формальное расположение m сигнальных точек на окружности с радиусом R, зависящем от мощности (энергии посылки) сигнала,на равных расстояниях с угловым интервалом 2*p/m радиан. Примеры совокупностей сигнальных точек-векторов для случаев m=2,4,8,16:
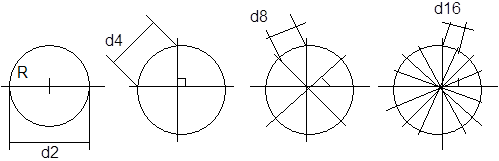

 а) б) в) г)
а) б) в) г)
Если на посылке передается гармоническое колебание с параметрами a,w,j, тогда
____________________
T
__ ó __ __
R=\/E= ôa^2*sin^2(w*t+j)dt =a*\/ T/ \/ 2
õ
0
Данное значение R совпадает с евклидовым расстоянием между центром окружности и любой точкой на ней. Для 2-х позиционного ФМ сигнала (рис. а) расстояние между сигланьными точками 2*\/E - это максимально возможное расстояние между точками круга с радиусом \/E. Оно полностью определяет потенциальную помехоустойчивость данной 2-х позиционной системы.
Расстояние между двумя гармоническими сигналами S1 и S2 длительностью Т1 отличающимися по фазе на угол j
d=(S1,S2)= (S1(t)-S2(t))^2dt = (a*sin(w*t+j)-a*sinw*t)^2dt =
______________ ____ _______
=\/ (a^2)*T(1-cosj) =\/2*E *\/1-cosj ,где E=(a^2)*T/2
Ниже приведена таблица расчетов рассояний dm между ближайшими вариантами сигнала в m-позиционных системах с ФМ и соответствующих проигрышей (по минимальному сигнальному расстоянию), текущей системы двухпозиционной (см. 7 стр 49.):
| Кратность манипуляции К | Число фаз m | Минимальная разнсть фаз | Минимальное евклидово расстояние между сигналами dm | d2/dm,дБ |
| 1 | 2 | p | 2*\/E | 0 |
| 2 | 4 | p/2 | \/2*E=1.41*\/E | 3.01 |
| 3 | 8 | p/4 | \/(2-\/2)E=0.765\/E | 8.34 |
| 4 | 16 | p/8 | \/(2--\/2+\/2)E= =0.39\/E | 14.2 |
| 5 | 32 | p/16 | \/(2--\/2+\/2+\/2)E= =0.196\/E | 20.2 |
Равномерное размещение всех сигнальных точек на окружности, т.е. использование равномощных сигналов, отличающихся лишь фазой, является оптимальным только для 2-х, 3-х и 4-х позиционных случаев. При m>4 оптимальными будут неравномощные сигналы, которые кроме отличия по фазе имеют различие по амплитуде. Размещены они равномерно, обычно внутри окружности, радиус которой определяется максимально допустимой энергией сигнала. С точки зрения теории модуляции такие сигналы относятся к сигналам с комбинированной модуляцией, при которой одновременнo изменяется несколько параметров сигнала. В данном случае амплитуда и фаза (сигналы с амплитудно-фазовой манипуляцией АФМн). Простейший принцип построения сигналов с АФМн состоит в том, что сигнальные точки размещаются на двух концентрических окружностях. Однако, этот путь не всегда приводит к оптимальному результату. Например: 8-ми позиционный сигнал с АФМн:
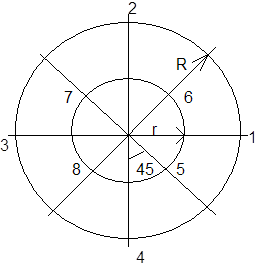
___
4 сигнала размещены на окружности с радиусом R=\/E , а 4 на окружности r<R со сдвигом по фазе p/4 (сигнальные точки расположены рядом с их соответствующими номерами). Данная совокупность сигналов оптимизируется по критерию максимума минимального расстояния между сигналами, путём выбора отношения радиусов R и r. Оптимальное отношение R/r=1.932 определяется чисто из геометрических соображений: чем больше r, тем больше расстояние между сигнальными точками окружности радиуса r, но тем меньше расстояния между этими точками и токами окружности радиуса R. Пэтому искомый максимум R/r достигается тогда, когда эти расстояния будут равны т.е. равносторонним будет треугольник 854, а это будет только тогда, когда искомое отношение равно указанному. При этом оптимальном отношении минимальное расстояние между сигналами d8=0.73\/E (см.7.стр.51). Это расстояние меньше,чем у системы 8-ми позиционных ФМн-сигналов, расположенных на одной окружности радиуса R(см. последнюю таблицу). Таким образом, в случае трехкратной системы размещение сигнальных векторов на двух концентрических окружностях не дает выигрыша. Оптимальным по критерию максимума минимального расстояния оказывается простейшая 8-ми позиционная система с АФМн, у которой 7 сигнальных точек размещены на окружности радиуса R=\/E , а восьмой сигнал равен нулю:
, а восьмой сигнал равен нулю:
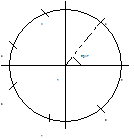
МИНИМАЛЬНОЕ РАССТОЯНИЕ У ТАКОЙ СИСТЕМЫ d8=0.86\/E, ЧТО БОЛЬШЕ, ЧЕМ d8 ФМн.
Далее рассмотрим 16-позиционные АФМн-сигналы.
Расстояние между ближайшими сигнальными точками в 16-ти позиционной ФМн системе d16=0.39\/E, что соответствует проигрышу в 14.2 дБ по сравнению с 2-х позиционной (см. посл. табл.). В круге данного радиуса можно построить лучшую систему сигналов с АФМн. Примером построения такой системы является система, у которой нечётные сигналы равномерно размещены на окружности большого радиуса с интервалом p/4, а чётные -- с тем же интервалом на окружности меньшего радиуса, но с общим сдвигом по фазе относительно нечётных на угол p/8:

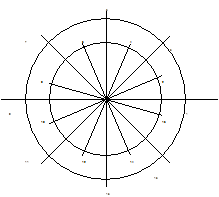
Оптимальное соотношение между радиусами R/r=1.587. При этом отношении минимальное расстояние между сигналами d16=0.482\/E. Таким образом минимальное расстояние между сигналами в 16-ти позиционной АФМн сигнале больше, чем в аналогичной ФМн. Следовательно и помехоустойчивость в 16-типозиционной АФМн системе выше при таком расположении векторов, чем в аналогичной ФМн системе, при равномерном размещении сигнальных точек на окружности.
Другим ярким примером 16-ти позиционных АФМн сигналов является система, в которой сикнальные точки размещены в узлах квадратной решетки:

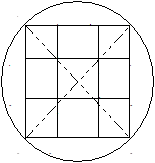
Минимальное расстояние между сигнальными точками (d16=0.47\/E) хоть и меньше, чем в предыдущем примере, но такой сигнал удобен с точки зрения практической реализации.
При всех своих достоинствах АФМн сигналы имеют довольно серьёзный недостаток -- это неравномощность вариантов. По этой причине возникают определённые трудности как при их передачи(особенно при наличии нелинейных преобразований, которые обычно имеют место, например на БРТР), так и при оптимальной обработке. По этим причинам в рассматриваемой здесь системе не будем переходить от 8-ми позиционных ФМн сигналов к аналогичным АФМн (хотя необходимо отметить относительно весомое превосходство последних по помехоустойчивости). Однако, в том случае, если необходимо в одном БРТР ретранслировать число станций большее, чем 65 (при Pош=const), то придётся сделать переход к сигналам с шестнадцатью позициями фазы, т.к. при возрастании m в сигналах с ФМн, при равномерном расположении сигнальных точек на окружнсти, резко ухудшается помехоустйчивость. 8-ми позиционные сигналы АФМн довольно часто нахoдят применение именно по этой причине.
0 комментариев