ПРАКТИЧЕСКАЯ ЧАСТЬ
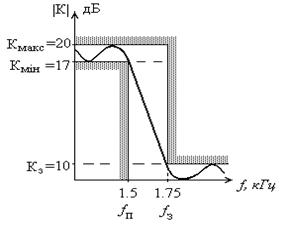
Тип фильтра определяется допустимой неравномерностью его АЧХ в полосе пропускания. При С =0 выбирается фильтр Баттерворта, а при С 0 - фильтр Чебышева Для С = 3дБ выбираем фильтр Чебышева.
Необходимый порядок фильтра ( n ) выбирается исходя из: минимального затухания в полосе заграждения З и допустимой неравномерности его АЧХ в полосе пропускания С .
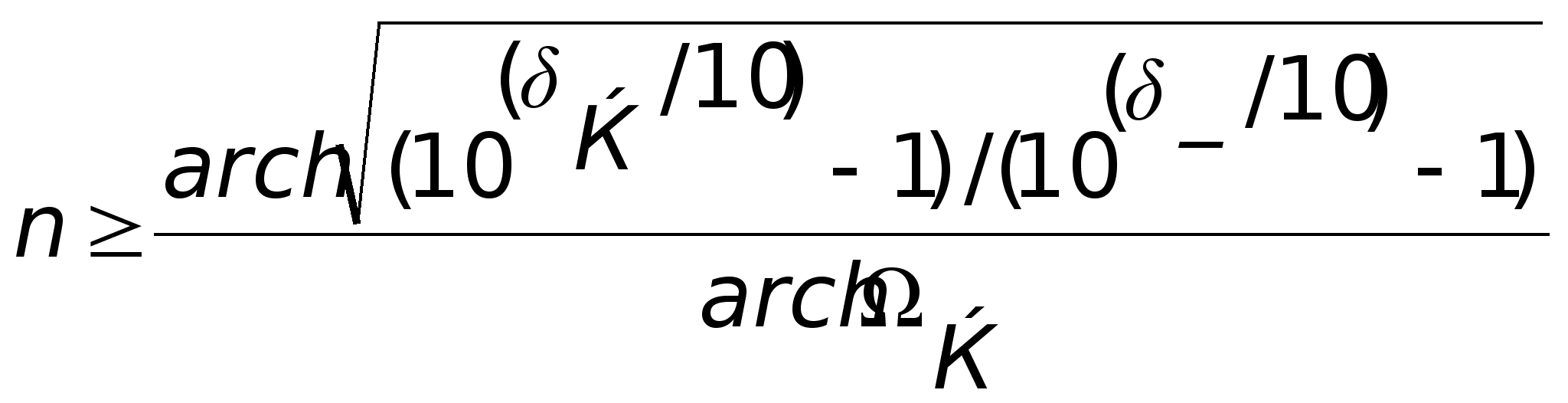 ,
где
,
где
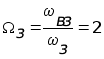
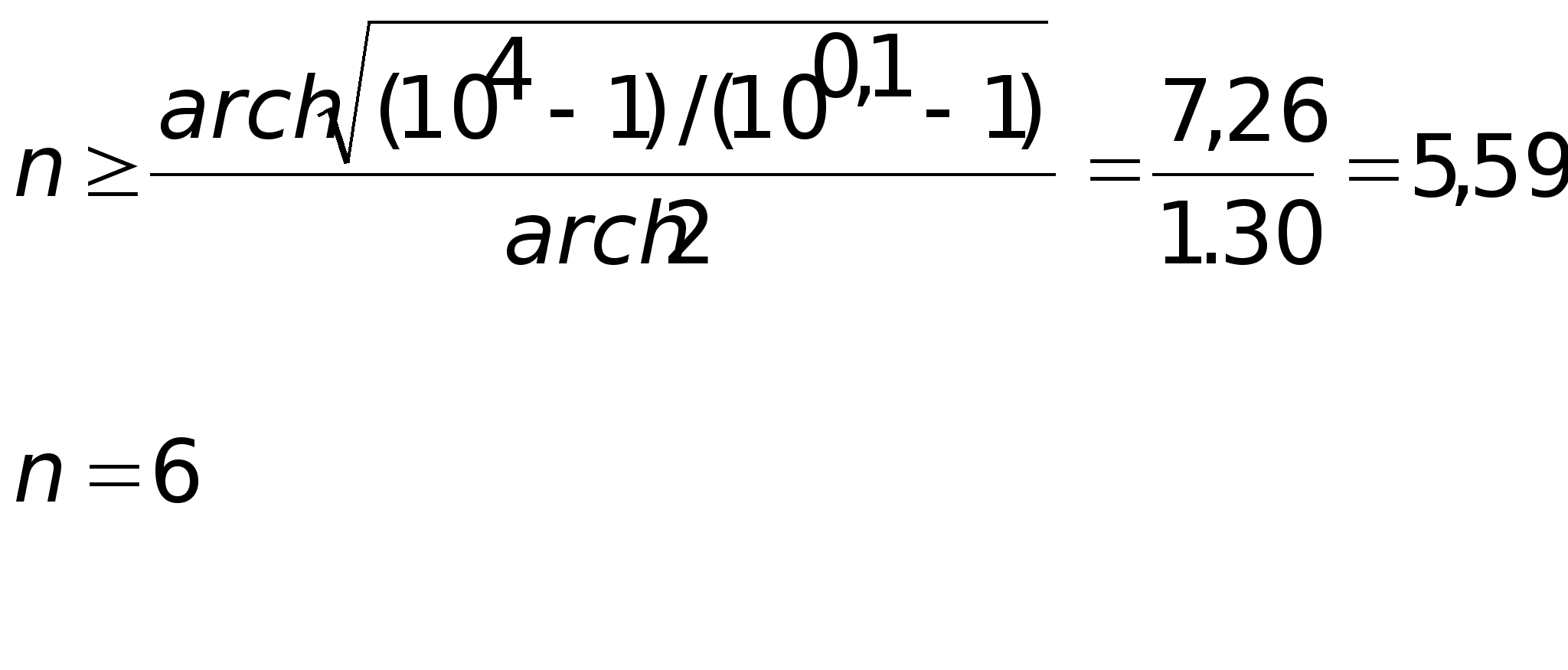
Рассмотрим каскадную реализацию фильтра в виде последовательного соединения взаимонезаменяемых звеньев второго порядка (т.к. n=6 - четное), количество звеньев определяется соотношением
![]() (звена
второго
порядка)
(звена
второго
порядка)
Определим значения коэффициентов ai , bi полинома, аппроксимирующего передаточную функцию фильтра и добротности полюсов звеньев фильтра:
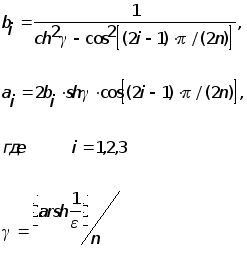
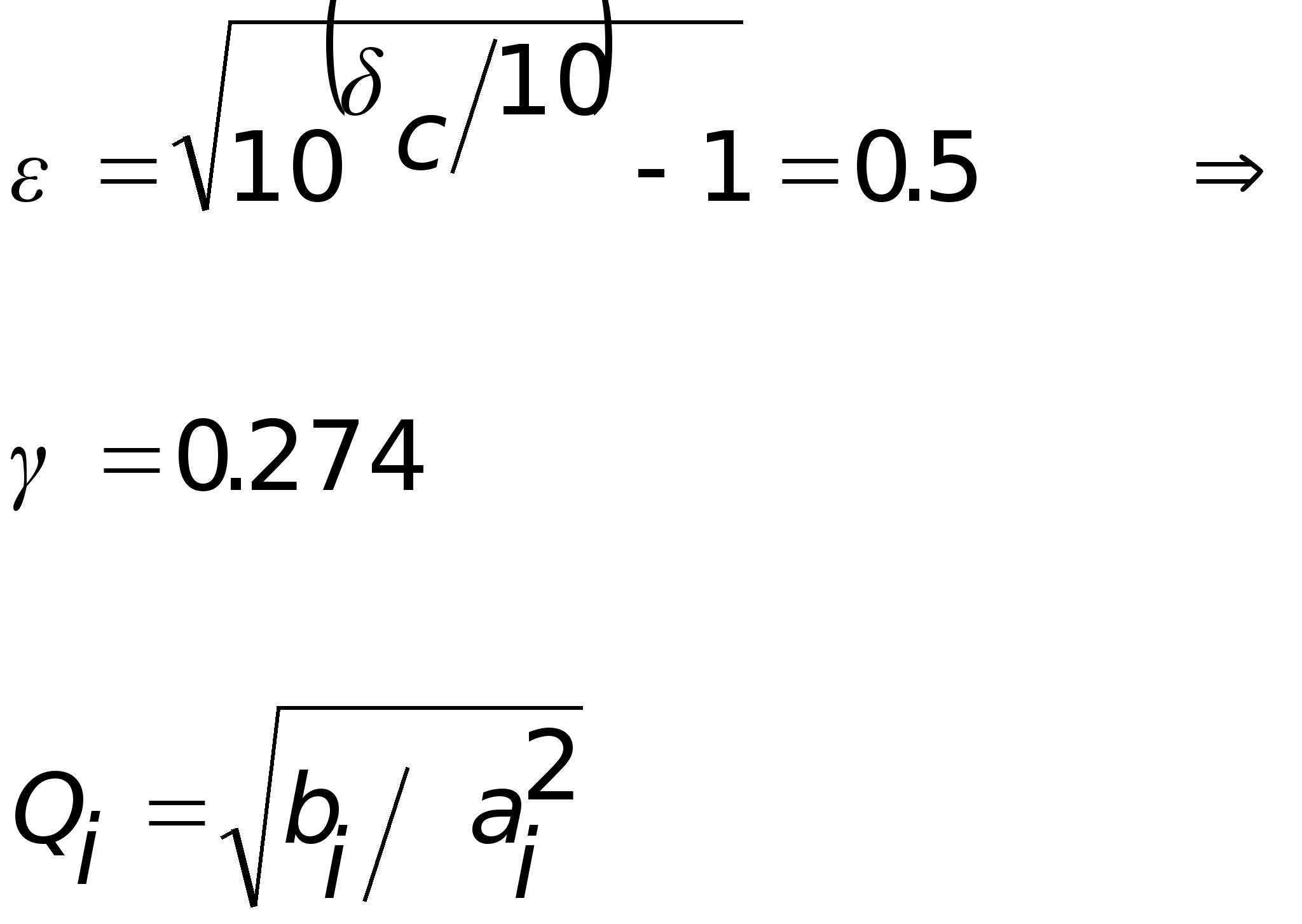
Для i=1 (первое звено) получим:
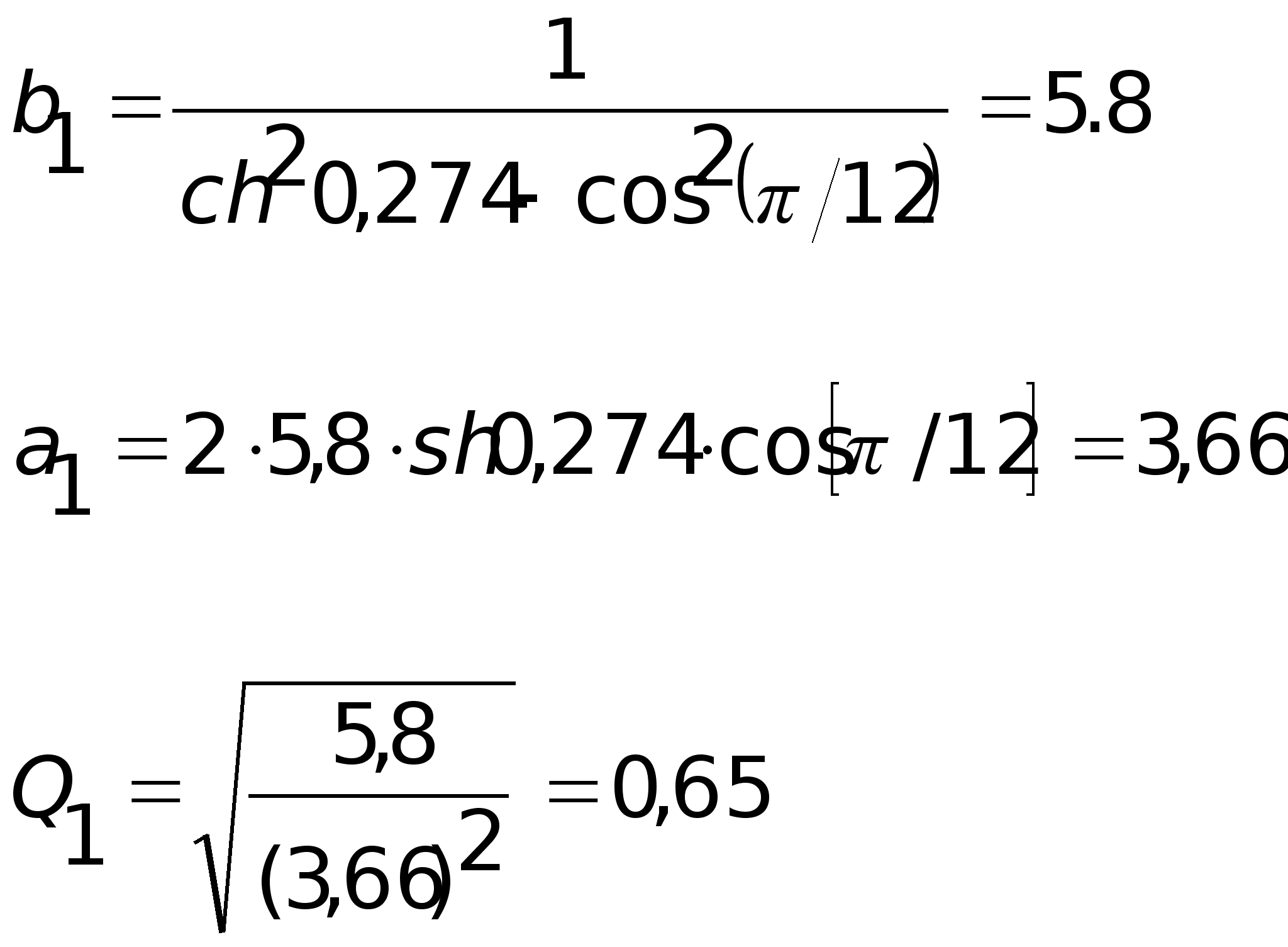
Для i=2 (второе звено) получим:
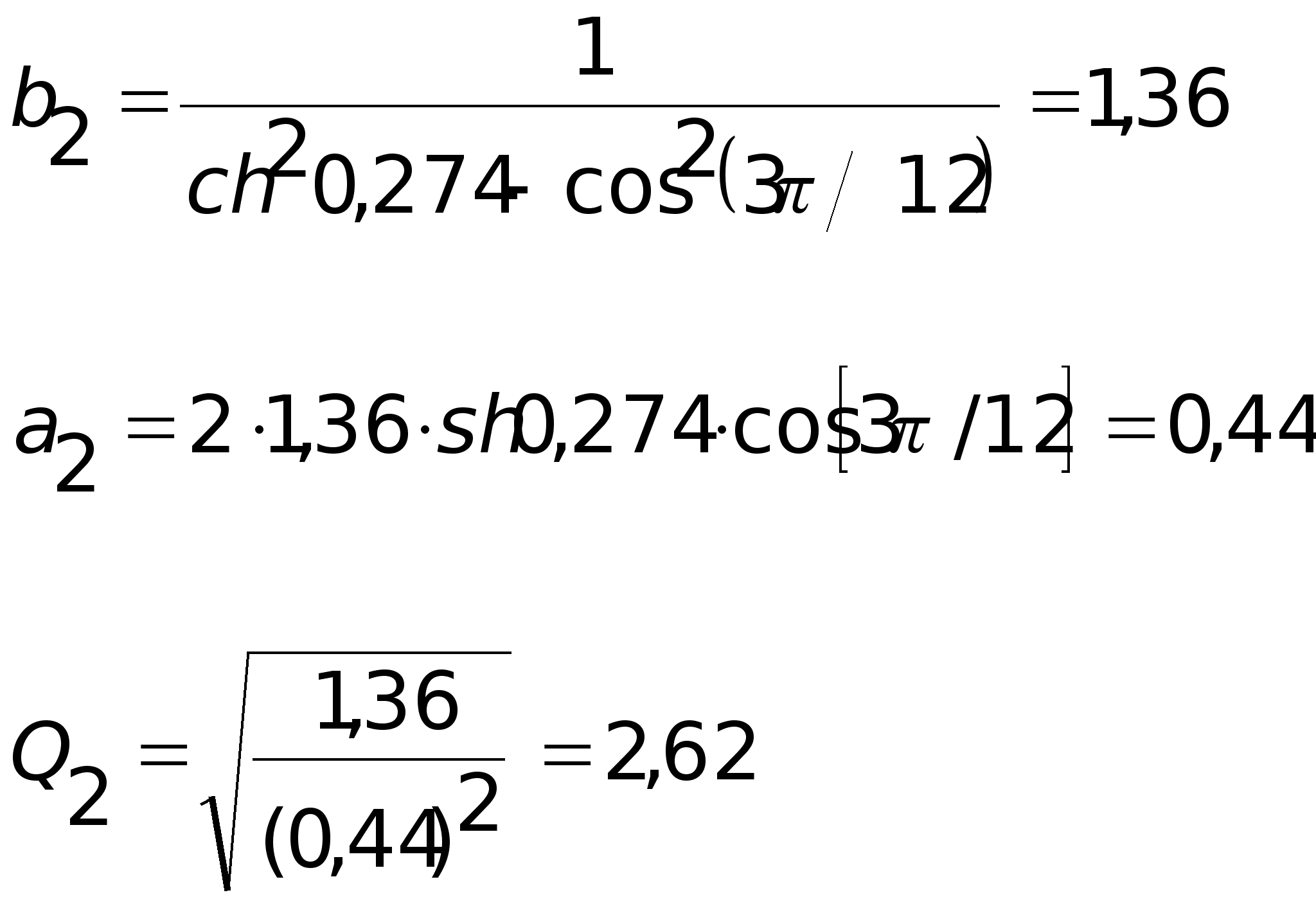
Для i=3 (третье звено) получим:
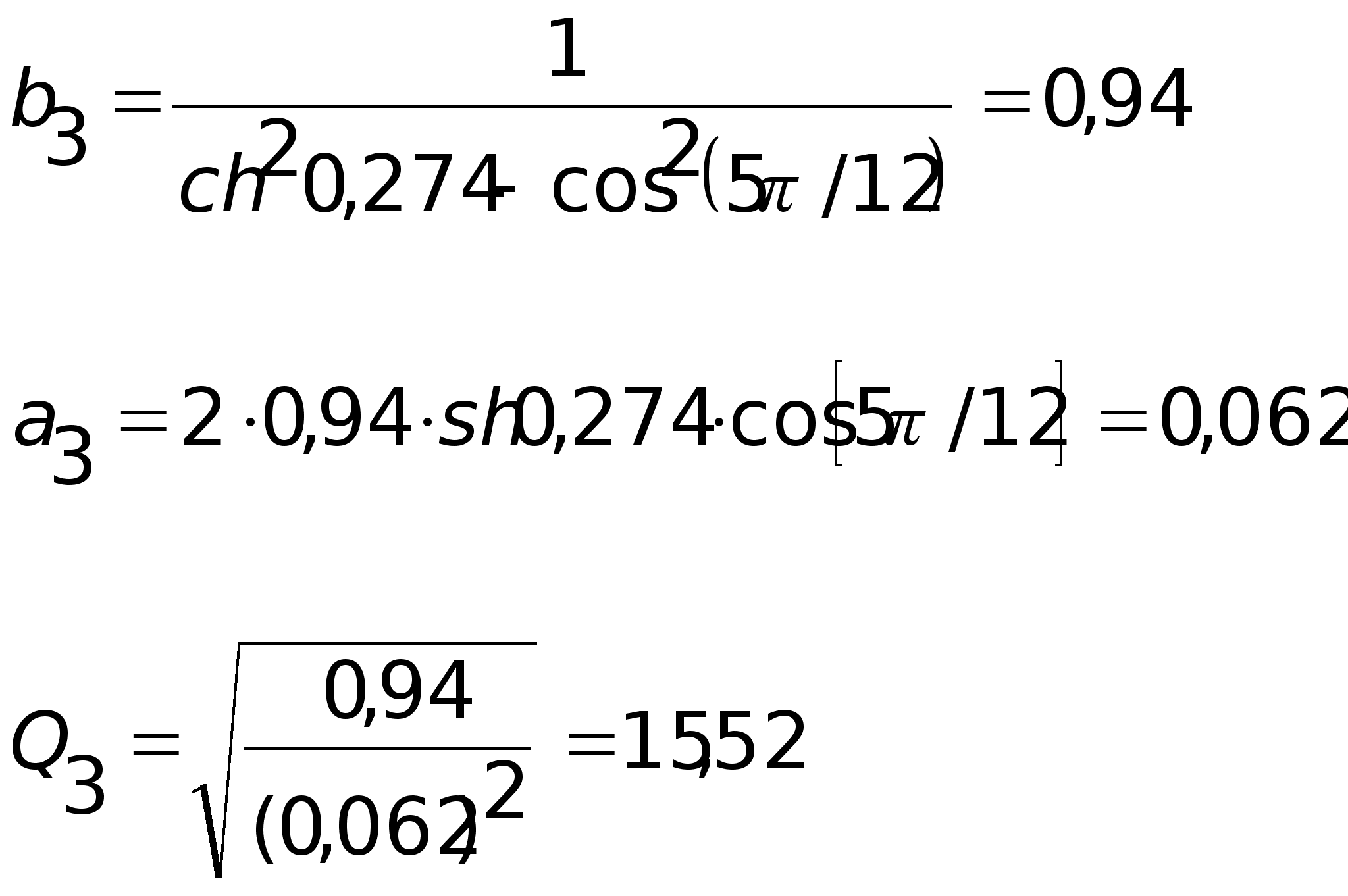
Расчет звеньев фильтра:
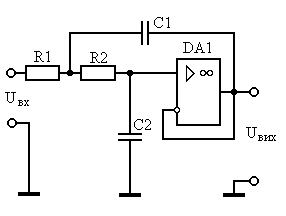
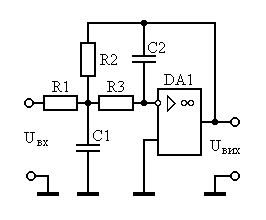
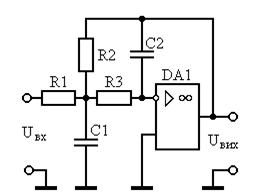
Исходя из добротностей для всех звеньев подходит схема звена второго порядка на повторителе:
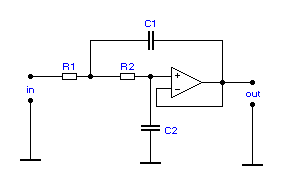
Передаточная характеристика имеет вид :
![]()
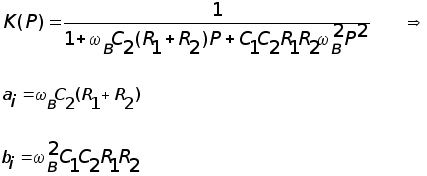
![]()
Отсюда при извесных ai , bi в рассчитываются элементы схемы:
Выбираем значение емкости С1 близкое к
![]()
и номинальное значение С2, удовлетворяющее условию:
![]()
для первого звена
![]()
для второго звена
![]()
для третьего звена
![]()
Рассчитываем величины R1 и R2 по соотношениям:
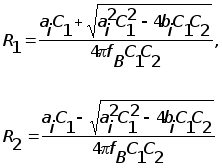
для первого звена
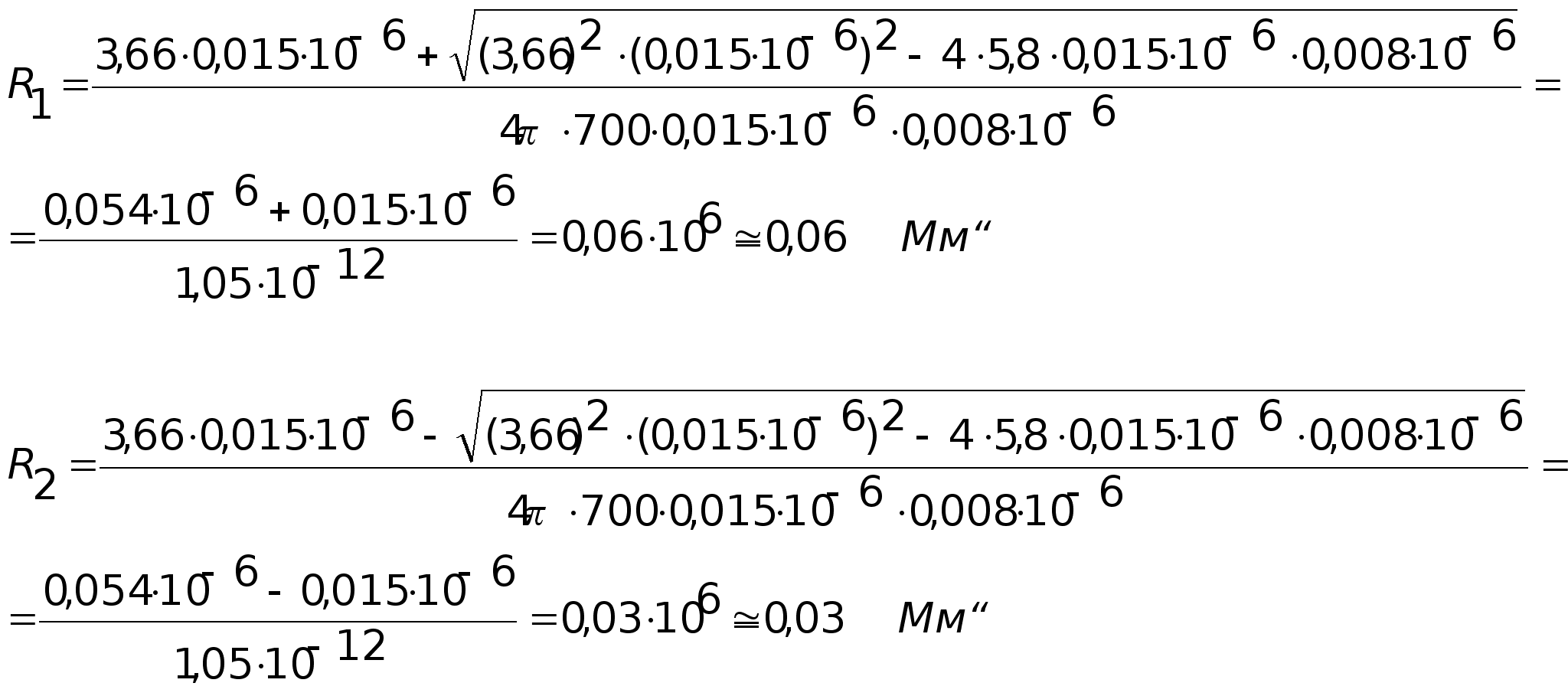
для второго звена
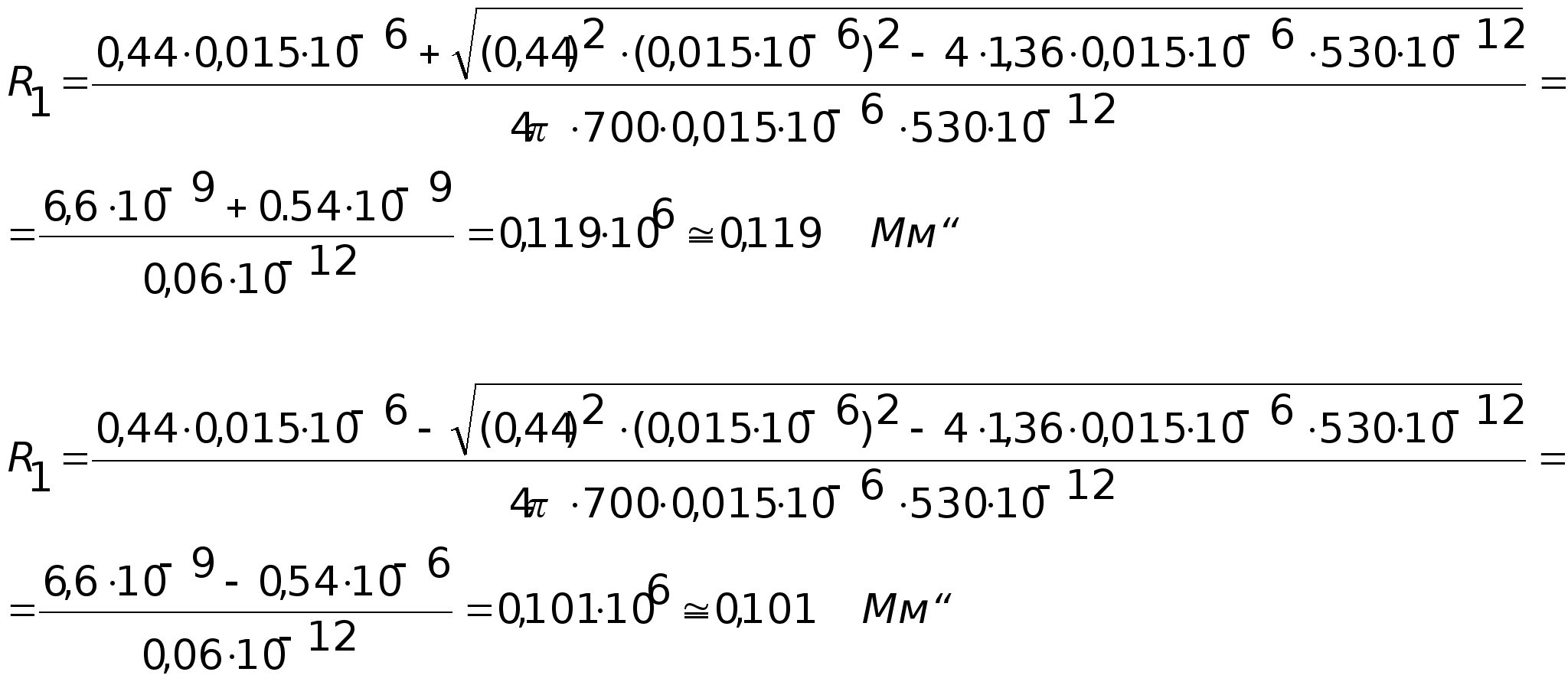
для третьего звена

Исходя из полученных результатов выбираем операционный усилитель : основными параметрами являются входное сопротивление, диапазон частот , минимальное сопротивление нагрузки.
Приемлемым является ОУ - 140УД6
| 140УД6 | |
| Коэффициент усиления K, В/мВ | 70 |
| Напряжение смещения нуля Uсм, мВ | 4 |
| Входные токи Iвх, нА | 30 |
| Разность входных токов Iвх, нА | 10 |
| Частота единичного усиления f1 ,МГц | 1 |
| Коэффициент ослабления синфазного сигнала, дБ | 80 |
| Максимальный выходной ток Iвых max, мА | 25 |
| Входное сопротивление Rвх, Мом | 2 |
| Потребляемый ток Iпот, мА | 2.8 |
| Максимальное выходное напряжение Uвых max, В | 12 |
Теоретическая часть
1.Введение
Простые RC - фильтры нижних или верхних частот обеспечивают пологие характеристики коэффициента передачи с наклоном 6Дб/октава после точки, соответствующей значению коэффициента передачи -3Дб. Для многих целей такие характеристики вполне подходят, особенно в тех случаях, когда сигнал, который должен быть подавлен, далеко сдвинут по частоте относительно полосы пропускания. В качестве примеров можно привести шунтирование радиочастотных сигналов в схемах усиления звуковых частот, «блокирующие» конденсаторы для устранения постоянной составляющей и разделения модулирующей и несущей частот.
Однако часто возникает необходимость в фильтрах с более пологой характеристикой в полосе пропускания и более крутыми склонами. Такая потребность существует всегда, когда надо отфильтровать сигнал от помехи близкой по частоте.
Активные фильтры можно использовать для реализации фильтров нижних (АФНЧ) и верхних (АФВЧ) частот, полосовых и полосно подавляющих фильтров, выбирая тип фильтра в зависимости от наиболее важной характеристики, таких, как максимальная равномерность усиления в полосе пропускания, крутизна переходной области характеристики или независимость времени запаздывания от частоты. Кроме того можно построить как «всепропускающие фильтры» с плоской амплитудно-частотной характеристикой. Но не стандартной фазо-частотной характеристикой (они также известны как «фазовые корректоры»), так и наоборот - фильтры с постоянным фазовым сдвигом, но с произвольной амплитудно-частотной характеристикой
Типы фильтров
Предположим, что требуется фильтр нижних частот с плоской характеристикой в полосе пропускания и резким перходом в полосе подавления. Окончательный же наклон характеристики в полосе задерживания всегда будет 6n дБ/октава, где n-количество «полюсов». На каждый полюс необходим один конденсатор (или катушка индуктивности), поэтому требования к окончательной скорости спада частотной характеристики фильтра, грубо говоря, определяют его сложность.
Теперь предположим, что мы решили использовать 6-полюсный фильтр нижних частот. Нам гарантирован окончательный спад характеристики на высоких частотах 36 дБ/октава. В свою очередь теперь можно оптимизировать схему фильтра в смысле обеспечения максимально плоской характеристики в полосе пропускания за счет уменьшения крутизны перехода от полосы пропускания к полосе задерживания. С другой стороны, допуская некоторую неравномерность характеристики в полосе пропускания, можно добиться более крутого перехода от полосы пропускания к полосе задерживания. Третий критерий, который может оказаться также важным, описывает способность фильтра пропускать сигналы со спектром, лежащим в полосе пропускания, без искажений их формы, вызываемых фазовыми сдвигами. Можно также интересоваться временем нарастания, выбросом и временем установления.
Извесны методы проектирования фильтров, пригодные для оптимизации любой из этих характеристик или их комбинации. Действительно разумный выбор фильтра происходит не так, как описано выше; как правило, сначала задаются требуемая равномерность характеристики в полосе попускания и необходимое затухание на некоторой частоте вне полосы пропускания и некоторые другие параметры. После этого выбирается наиболее подходящая схема с количеством полюсов, достаточным для того, чтобы удовлетворялись все эти требования. Имеется три наиболее популярных схемы фильтров, а именно фильтр Баттерворта (максимально плоская характеристика в полосе пропускания), фильтр Чебышева (наиболее крутой переход от полосы пропускания к полосе подавления) и фильтр Бесселя (максимально плоская характеристика времени запаздывания). Любой из этих типов фильтров можно реализовать с помощью различных схем фильтров. Все они разным образом годятся для построения фильтров верхних и нижних частот, а так же полосовых фильтров.
Фильтры Баттерворта и Чебышева
Фильтр Баттерворта обеспечивает наиболее плоскую характеристику в полосе пропускания, что достигается ценой плавности характерисатики в переходной области, т.е. между полосами пропускания и задерживания. Его амплитудно частотная характеристика задаётся следующей формулой:
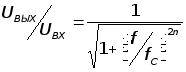 ,
,
где n - определяет порядок фильтра (число полюсов). Увеличение числа полюсов дает возможность увеличить крутизну спада от полосы пропускания к полосе подавления.
Выбирая фильтр Баттерворта мы ради плоской характеристики поступаемся всем остальным. Его характеристика идет горизонтально, начиная от нулевой частоты, перегиб ее начинается на частоте среза fC - эта частота обычно соответствует точке -3 дБ.
В большинстве применений самым существенным обстоятельством является то, что неравномерновть характеристики в полосе пропускания недолжна превыщать некоторой величины, скажем 1 дБ. Фильтр Чебышева отвечает этому требованию, при этом допускается некоторая неравномерность харкктеристики по всей полосе пропускания, но при этом сильно увеличивается острота её излома. Для фильтра Чебышева задают число полюсов и неравномерность в полосе пропускания. Допуская увеличение неравномерности в полосе пропускания., получаем более острый излом. Амплитудная характеристика этого фильтра описывается уравнением:
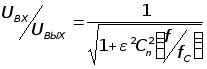 ,
,
где Сn - полином Чебышева первого рода степени n, а - константа, определяющая неравномерность характеристики в полосе её пропускания. Фильтр Чебышева, как и фильтр Баттерворта имеет фазо-частотные характеристики далекие от идеальных.
На самом деле фильтр Баттерворта с максимально плоской характеристикой в полосе пропускания не так привлекателен, как это может показаться, поскольку в любом случае приходится мириться с некоторой неравномерностью характеристики в полосе пропускания (для фильтра Баттерворта это будет постепенное понижение характеристики при приближении к частоте fc, а для фильтра Чебышева - пульсации, распределенные по всей полосе пропускания). Кроме того, активные фильтры, построенные из элементов, номиналы которых имеют некоторый допуск, будут обладать характеристикой, отличающейся от рассчетной, а это значит, что в действительности на характеристике фильтра Баттерворта всегда будет иметь место некоторая неравномерность в полосе пропускания.
В свете вышеизложеного весьма рациональной структурой является фильтр Чебышева. Иногда его называют равноволновым фильтром, так как его характеристика в области перехода имеет большую крутизну за счет того, что в полосе пропускания распределено несколько равновеликих пульсаций, число которых возрастает вместе с порядком фильтра. Даже при сравнительно малых пульсациях (порядка 0,1дБ ) фильтр Чебышева обеспечивает намного большую крутизну характеристики в преходной области, чем фильтр Баттерворта. Чтобы выразить эту разницу количественно, предположим, что требуется фильтр с неравномерностью характеристики в полосе пропускания не более 0,1 дБ и затуханием на частоте, отличающецся на 25% от граничной частоты пропускания. Расчет показывает, что в этом случае требуется 19-полюсной фильтр Баттерворта или всего лишь 8-полюсный фильтр Чебышева.
Мысль о том, что можно мириться с пульсациями характеристики в полосе пропускания ради крутизны переходного участка характеристики, доводиться до своего логического завершения в идее так называемого элептического фильтра (или фильтра Кауэра), в котором допускаются пульсации характеристики как в полосе пропускания, так и в полосе задерживания ради обеспечения крутизны переходного участка даже большей, чем у характеристики фильтра Чебышева. С помощью ЭВМ можно сконструировать эллиптические фильтры так же просто, как и классические фильтры Чебышева и Баттерв
Похожие работы
... на активные потери (затухание в диэлектрике) в фильтре, с увеличением этих параметров, увеличиваются потери в диэлектрике, что приводит к снижению КПД СВЧ устройства. Данный фильтр низкой частоты должен работать при температуре окружающей среды t0 = −30 0С…+50 0С. Годовая программа выпуска данного устройства 150 шт. Основным достоинством полосковых и микрополосковых линий и устройств СВЧ ...
... = 6,66 на различные уровни входного гармонического воздействия Рис. Реакция схемы при Q = 10,8 на различные уровни входного гармонического воздействия 5. Синтез ФНЧ третьего порядка с дополнительными RC-цепями Фильтры нижних частот в СВЧ диапазоне образуют отдельный и важный в практическом отношении класс устройств частотной селекции. Достаточно отметить каналообразующие фильтры при ...
... доступны. 5. Низкочастотные фильтры можно построить на элементах малых номиналов. Целью данной курсовой работы является проектирование активного фильтра высоких частот основанного на интегральных операционных усилителях. 1. Существующие виды активных ВЧ фильтров Рассмотрим методы реализации различных типов функций цепи, основанные на использовании схем фильтров, включающих как активные, ...
... соединения ФНЧ- ІІ, как на рис. 2.2: Рисунок 2.2 – Структурная схема графа Мезона Выбор схемного решения Схемным решением для данного устройства будет фильтр низкой частоты второго порядка с многопетлевой обратной связью, т.к. он обеспечивает небольшую чувствительность к отклонению номиналов элементов. Используем 3 таких звена, соединённых последовательно. Рисунок 2.3 – ФНЧ-ІІ с ...
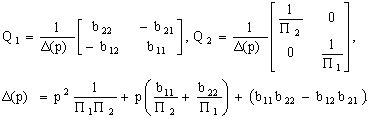


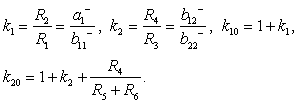
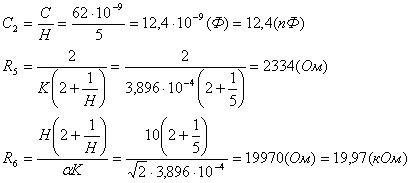
0 комментариев