Навигация
Міністерство освіти і науки України
Харківський національний університет радіоелектроніки
Кафедра радіоелектронних пристроїв
Курсова робота
Пояснювальна записка
Фільтр нижніх частот
Виконав:
ст. гр. РТ-07-1
Рубан В.В.
Керівник:
Звягінцев О.Ю.
Харків 2009
Реферат
Пояснительная записка: 21 с., 7 рис.
Цель работы - синтез схемы активного RC-фильтра и расчет компонентов схемы.
Метод исследования - аппроксимация АЧХ фильтра полиномом Чебышева.
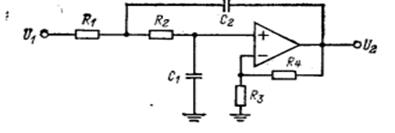
Аппроксимированная передаточная функция реализована с помощью активного фильтра. Фильтр построен на трёх активных каскадах. В фильтре использован инвертирующий усилитель с конечным усилением, который реализован на операционном усилителе.
Результаты работы могут использоваться для синтеза фильтров радиотехнической аппаратуры.
Прогнозируемые предложения относительно развития объекта исследования - поиск оптимальных схем фильтров.
АКТИВНЫЙ ФИЛЬТР, АППРОКСИМАЦИЯ, ФИЛЬТР ЧЕБЫШЕВА, ОПЕРАЦИОННЫЙ УСИЛИТЕЛЬ, ПЕРЕДАТОЧНАЯ ХАРАКТЕРИСТИКА
Содержание
Перечень условных сокращений. 4
Введение. 5
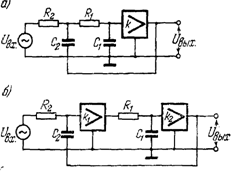
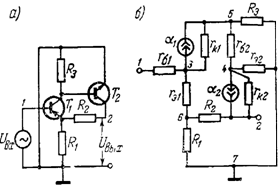
1 Обзор аналогичных схем. 7
2 Выбор схемы фильтра. 9
3 Топологическая модель фильтра. 13
4 Расчет элементов схемы.. 14
5 Методика настройки и регулировки фильтра. 16
Выводы.. 17
Перечень ссылок. 18
Приложение. 19
Перечень условных сокращений
ОУ – операционный усилитель;
АЧХ – амплитудно-частотная характеристика;
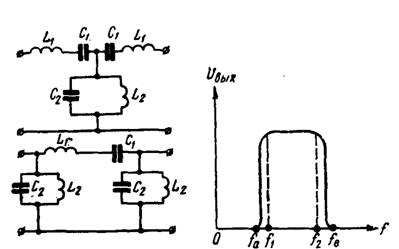
ПФ – полосовой фильтр;
ФВЧ – фильтр высоких частот;
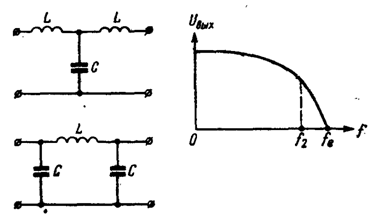
ФНЧ – фильтр низких частот.
Введение
Активный фильтр - один из видов аналоговых электронных фильтров, в котором присутствует одна или несколько активных компонент, к примеру транзистор или операционный усилитель. Эти обладающие частотной избирательностью схемы используются для усиления или ослабления определенных частот в звуковой аппаратуре, в генераторах электромузыкальных инструментов, в сейсмических приборах, в линиях связи и т.п.
В активных фильтрах используется принцип отделения элементов фильтра от остальных электронных компонент схемы. Часто бывает необходимо, чтобы они не оказывали влияния на работу фильтра.
Существует несколько различных типов активных фильтров, некоторые из которых также имеют и пассивную форму:
* Фильтр высоких частот — не пропускает частоты ниже частоты среза.
* Фильтр низких частот — не пропускает частоты выше частоты среза.
* Полосовой фильтр — не пропускает частоты выше и ниже некоторой полосы.
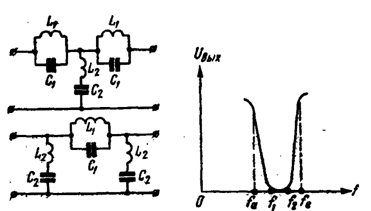
* Режекторный фильтр — не пропускает определённую ограниченную полосу частот.
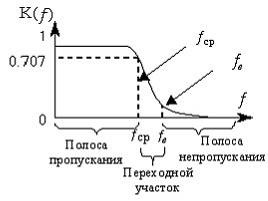
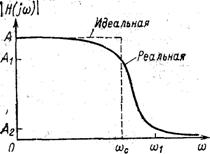
С помощью активных RC – фильтров нельзя получить идеальные формы частотных характеристик в виде прямоугольников со строго постоянным коэффициентом передачи в полосе пропускания, бесконечным ослаблением в полосе подавления и бесконечной крутизной спада при переходе от полосы пропускания к полосе подавления. Проектирование активного фильтра всегда представляет собой поиск компромисса между идеальной формой характеристики и сложностью её реализации. Это называется «проблемой аппроксимации». Во многих случаях требования к качеству фильтрации позволяют обойтись простейшими фильтрами первого или второго порядка. Проектирование фильтра в этом случае сводится к выбору схемы с наиболее подходящей конфигурацией и последующему расчету значений номиналов элементов для конкретных частот.
Данные проблемы рассматриваются в курсовой работе.
1 Обзор аналогичных схем
Фильтр Баттерворта обеспечивает наиболее плоскую характеристику в полосе пропускания, что достигается ценой плавности характеристики в переходной области, т.е. между полосами пропускания и задерживания. Его амплитудно-частотная характеристика задаётся следующей формулой:
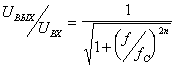 ,
,
где n - определяет порядок фильтра (число полюсов). Увеличение числа полюсов дает возможность увеличить крутизну спада от полосы пропускания к полосе подавления.
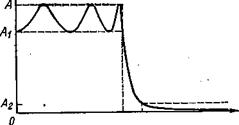
Выбирая фильтр Баттерворта мы ради плоской характеристики поступаемся всем остальным. Его характеристика идет горизонтально, начиная от нулевой частоты, перегиб ее начинается на частоте среза fC - эта частота обычно соответствует точке -3 дБ. Также фильтр не может обеспечить усиление сигнала в полосе пропускания.
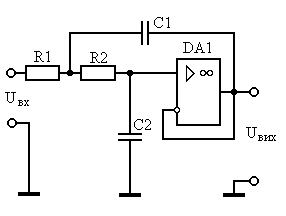
Рисунок 1.1 – ФНЧ Баттерворта
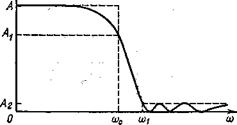
В большинстве применений самым существенным обстоятельством является то, что неравномерность характеристики в полосе пропускания не должна превышать некоторой величины, скажем 1 дБ. Фильтр Чебышева отвечает этому требованию, при этом допускается некоторая неравномерность характеристики по всей полосе пропускания, но при этом сильно увеличивается острота её излома. Для фильтра Чебышева задают число полюсов и неравномерность в полосе пропускания. Допуская увеличение неравномерности в полосе пропускания, получаем более острый излом. Амплитудная характеристика этого фильтра описывается уравнением:
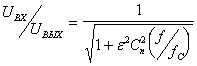 ,
,
где Сn - полином Чебышева первого рода степени n, а e - константа, определяющая неравномерность характеристики в полосе её пропускания. Фильтр Чебышева, как и фильтр Баттерворта имеет фазо-частотные характеристики далекие от идеальных.
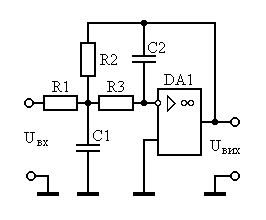
Рисунок 1.2 – ФНЧ Чебышева
Иногда фильтр Чебышева называют равноволновым фильтром, так как его характеристика в области перехода имеет большую крутизну за счет того, что в полосе пропускания распределено несколько равновеликих пульсаций, число которых возрастает вместе с порядком фильтра. Даже при сравнительно малых пульсациях (порядка 0,1дБ ) фильтр Чебышева обеспечивает намного большую крутизну характеристики в переходной области, чем фильтр Баттерворта. Чтобы выразить эту разницу количественно, предположим, что требуется фильтр с неравномерностью характеристики в полосе пропускания не более 0,1 дБ и затуханием на частоте, отличающейся на 25% от граничной частоты пропускания. Расчет показывает, что в этом случае требуется 19-полюсной фильтр Баттерворта или всего лишь 8-полюсный фильтр Чебышева.
Мысль о том, что можно мириться с пульсациями характеристики в полосе пропускания ради крутизны переходного участка характеристики, доводится до своего логического завершения в идее так называемого элептического фильтра (или фильтра Кауэра), в котором допускаются пульсации характеристики как в полосе пропускания, так и в полосе задерживания ради обеспечения крутизны переходного участка даже большей, чем у характеристики фильтра Чебышева.
Похожие работы
... и фильтра верхних частот. Полоса пропускания широкополосный фильтра - образуется благодаря перекрытию полос пропускания ФНЧ (0 -) и ФИЧ (- ) - (рис.7) Рисунок – 7 Образование полосы пропускания широкополосного фильтра 2 Пример расчета фильтра нижних частот на заданные параметры Аналитический метод расчета цепочных фильтров основан на нахождении оптимальных параметров фильтра по ...
... является эллиптический фильтр, характеристики которого значительно лучше характеристик фильтра Чебышева. Рис. 1.5.3. Амплитудно-частотная характеристика фильтра Чебышева шестого порядка Рис. 1.5.4. Амплитудно-частотная характеристика инверсного фильтра Чебышева шестого порядка 1.6 Фильтры нижних частот на ИНУН Схема на ИНУН, реализующая функцию фильтра нижних частот Баттерворта ...
... ; MOV X1, X ; MOV Y1, Y ; RETI ;возврат из подпрограммы обслуживания прерывания по входу END Исходные определения и ручной расчёт результатов работы программы: "Цифровой фильтр (нижних частот)". Разностное уравнение имеет вид: Представим уравнение в виде: , где , 1)Реализуемый коэффициент масштабирования (число без знака) при 8-разрядном формате беззнаковых коэффициентов: ;, ...
... целесообразно решать аппроксимационную задачу. Определим нормированную частоту ограничения фильтра, как отношение = = 0,6666. Нормированная частота в полосе задерживания обычного фильтра НЧ равна . Эта же частота в случае фильтра НЧ с ограниченной полосой пропускания рассчитывается по формуле Из кривых (рис. 1.) по вычисленной и заданным и а определим ...

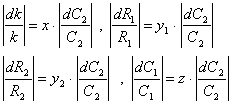
0 комментариев