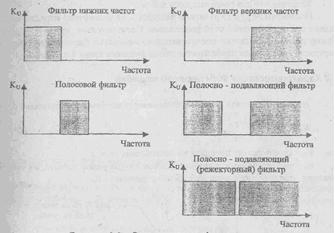
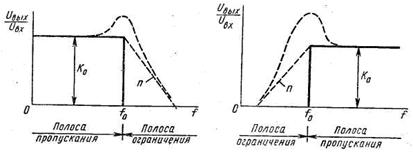
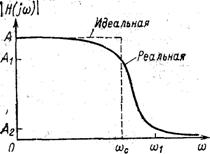
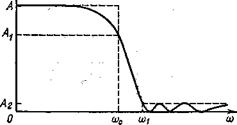
представляет собой устройство, которое пропускает сигналы в диапазоне частот с шириной полосы BW, расположенной приблизительно вокруг центральной частоты ω0 (рад/с), или f0=ω0/2π (Гц). На рисунке 1 изображены идеальная и реальная амплитудно-частотные характеристики. В реальной характеристике частоты ωL и ωU представляют собой нижнюю и верхнюю частоты среза и определяют полосу пропускания ωL≤ω≤ωU и её ширину BW= ωU-ωL.
В полосе пропускания амплитудно-частотная характеристика никогда не превышает некоторого определённого значения, например А на рисунке 1. Существует также две полосы задерживания 0≤ω≤ω1 и ω2≤ω, где значение амплитудно-частотной характеристики никогда не превышает заранее выбранного значения, скажем, А2. Диапазоны частот между полосами задерживания и полосой пропускания, а именно ωL<ω<ωU и ωL<ω<ωU, образуют соответствено нижнюю и верхнюю переходные области, в которых характеристика является монотонной.
Отношение Q=ω0/BW характеризует качество самого фильтра и является мерой его избирательности. Высокому значению Q соответствует относительно узкая, а низкому значению Q – относительно широкая полосы пропускания. Коэффициент усиления фильтра K определяется как значение его амплитудно-частотной характеристики на центральной частоте; таким образом, 
.
Передаточные функции полосно-пропускающих фильтров можно получить из нормированных функций нижних частот переменной S с помощью преобразования
.
Таким образом, порядок полосно-пропускающего фильтра в 2 раза выше, чем порядок соответствующего ему фильтра нижних частот и, следовательно всегда является чётным.
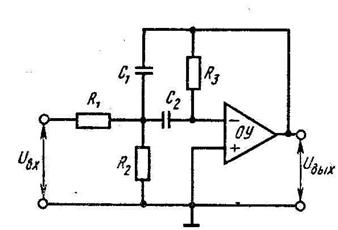
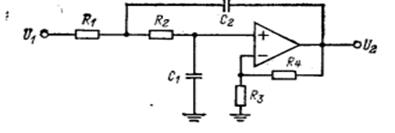
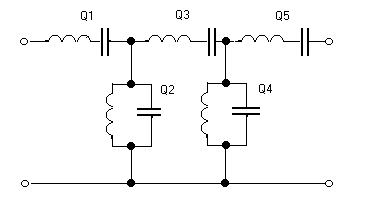
Схема с многопетлевой обратной связью (МОС) и бесконечным коэффициентом усиления, изображённая на рисунке 3 представляет собой один из наиболее простых полосно-пропускающих фильтров второго порядка. Она реализует функцию полосно-пропускающего фильтра при инвертирующем коэффициенте усиления.
Полосно-пропускающий фильтр с МОС, подобно его аналогам нижних и верхних частот, обладает минимальным числом элементов, инвертирующим коэффициентом усиления и способностью обеспечивать значение добротности Q≤10 при небольших коэффициентах усиления.
 |
Рисунок 1. Схема полосно-пропускающего фильтра с МОС
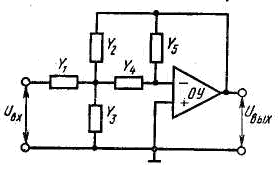
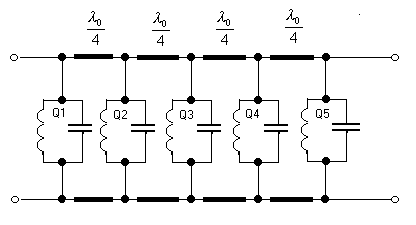
Схема на ИНУН, изображённая на рисунке 4 реализует функцию полосно-пропускающего фильтра второго порядка.
Этот полосно-пропускающий фильтр на ИНУН обеспечивает неинвертирующий коэффициент усиления и может реализовать значения добротности Q≤10.
Рисунок 2. Схема полосно-пропускающего фильтра на ИНУН
На рисунке 5 изображена биквадратная схема, которая реализует передаточную функцию полосно-пропускающего фильтра второго порядка.
Биквадратная схема требует бόльшего числа элементов, чем схема с МОС и на ИНУН, однако из-за её стабильности и прекрасных возможностях по настройке она очень популярна. На ней можно реализовать значения добротности вплоть до 100.
| |
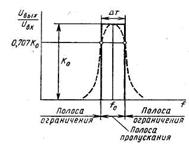
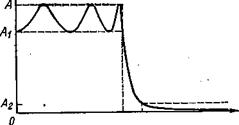
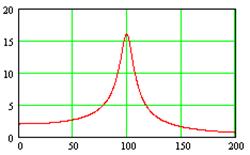
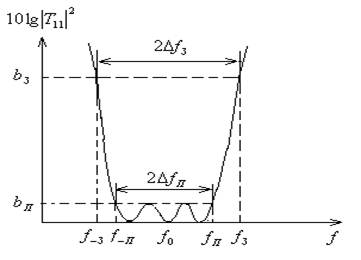
Настройка полосно-пропускающего звена второго порядка осуществляется наиболее просто, если имеется возможность наблюдать общий вид его амплитудно-частотной характеристики. Частоты f1 и f2 представляют собой точки по уровню 3 дБ.
РАСЧЁТ.
Для расчёта полосно-пропускающего фильтра второго порядка, соответствующего звену нижних частот второго порядка, обладающий заданной
Рисунок 3. Схема биквадратного полосно-пропускающего фильтра
центральной частотой f0 (Гц), или ω0=2πf0 (рад/с), коэффициентом усиления звена K и добротностью Q, необходимо выполнить следующие шаги.
1. Выбрать номинальное значение ёмкости C1 (предпочтительно близкое к значению 10/f0 мкФ) и номинальное значение ёмкости C2 (желательно равное C1).
2. Вычислить сопротивления:
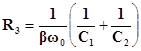
где ρ=K/Q; β=1/Q.
3. Выбрать номинальные значения сопротивлений, наиболее близкие к вычисленным значениям, и реализовать фильтр в соответствии со схемой рисунок 3.
КОММЕНТАРИИ
· Для обеспечения лучших рабочих характеристик номинальные значения элементов должны выбираться наиболее близкими к выбранным и вычисленным значениям. Рабочая характеристика не изменится, если значения всех сопротивлений умножить, а ёмкостей поделить на общий множитель.
· Входное полное сопротивление ОУ должно быть по крайней мере 10R3. Коэффициент усиления ОУ с разомкнутой обратной связью должен по крайней мере в 50 раз превышать значение амплитудно-частотной характеристики фильтра на частоте fa– наибольшей требуемой частоте в полосе пропускания, а его скорость нарастания (В/мкс) должна в 0,5ωа∙10–6 раз превосходить максимальный размах выходного напряжения.
· Инвертирующий коэффициент усиления 
. Следовательно, коэффициент усиления можно настроить, изменяя сопротивление R1. Для получения требуемой добротности Q изменяют сопротивление R2, и, изменяя одновременно сопротивления R2 и R3 в одинаковом процентном отношении, можно, не влияя на добротность Q, установить центральную частоту.
· Эту схему можно использовать только для фильтровых звеньев с коэффициентом усиления K и добротностью Q не более 10.
Похожие работы
... со строго постоянным коэффициентом передачи в полосе пропускания, бесконечным ослаблением в полосе подавления и бесконечной крутизной спада при переходе от полосы пропускания к полосе подавления. Проектирование активного фильтра всегда представляет собой поиск компромисса между идеальной формой характеристики и сложностью ее реализации. Это называется "проблемой аппроксимации". Во многих случаях ...
... Сравнительная характеристика различных реализаций синтезируемого фильтра. 17 Литература..................................................................................................................................................................... 18 Задание 1. Представить данные на синтез частотно-избирательного фильтра в графической форме с использованием нормированной ...
... является эллиптический фильтр, характеристики которого значительно лучше характеристик фильтра Чебышева. Рис. 1.5.3. Амплитудно-частотная характеристика фильтра Чебышева шестого порядка Рис. 1.5.4. Амплитудно-частотная характеристика инверсного фильтра Чебышева шестого порядка 1.6 Фильтры нижних частот на ИНУН Схема на ИНУН, реализующая функцию фильтра нижних частот Баттерворта ...
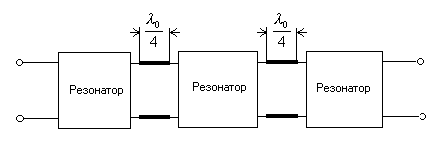
... их как в теоретическом, так и экспериментальных аспектах. Учитывая общую тенденцию миниатюризации радиотехнических СВЧ систем, увеличение концентрации энергии электромагнитного поля и непрерывное повышение требований в части электромагнитной совместимости (ЭМС), комплексное решение задач проектирования и практической реализации оптимальных СВЧ фильтров, а также обобщение накопленного опыта их ...
0 комментариев