Навигация
Частотно-избирательные фильтры. Фильтр нижних частот Чебышева
Южно-Уральский государственный университет
Приборостроительный факультет
Кафедра РТС
Курсовая работа
ЧАСТОТНО-ИЗБИРАТЕЛЬНЫЕ ФИЛЬТРЫ. ФИЛЬТР НИЖНИХ ЧАСТОТ ЧЕБЫШЕВА
Челябинск 2007
1. Основная часть
1.1 Частотно-избирательные фильтры
В большинстве случаев электрический фильтр представляет собой частотно-избирательное устройство. Следовательно, он пропускает сигналы определенных частот и задерживает или ослабляет сигналы других частот. Наиболее общими типами частотно-избирательных фильтров являются фильтры нижних частот (которые пропускают низкие частоты и задерживают высокие частоты), фильтры верхних частот (которые пропускают высокие частоты и задерживают низкие частоты), полосно-пропускающие фильтры (которые пропускают полосу частот и задерживают те частоты, которые расположены выше и ниже этой полосы) и полосно-заграждающие фильтры (которые задерживают полосу частот и пропускают частоты, расположенные выше и ниже этой полосы).
Более точно характеристику частотно-избирательного фильтра можно описать, рассмотрев его передаточную функцию
![]()

Рис. 1.1
Величины V1 и V2 представляют собой соответственно входное и выходное напряжения, как показано на общем изображении фильтра на рис. 1.1.
Для установившейся частоты ![]() передаточную функцию можно переписать в виде
передаточную функцию можно переписать в виде
![]()
где ![]() – модуль передаточной функции или амплитудно-частотная характеристика;
– модуль передаточной функции или амплитудно-частотная характеристика;
![]() - фазо-частотная характеристика, а частота ω (рад/с) связана с частотой f (Гц) соотношением ω = 2πf.
- фазо-частотная характеристика, а частота ω (рад/с) связана с частотой f (Гц) соотношением ω = 2πf.
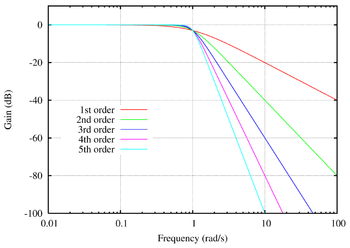
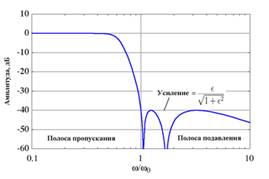
Диапазоны или полосы частот, в которых сигналы проходят, называются полосами пропускания и в них значение амплитудно-частотной характеристики ![]() относительно велико, а в идеальном случае постоянно. Диапазоны частот, в которых сигналы подавляются, образуют полосы задерживания и в них значение амплитудно-частотной характеристики относительно мало, а в идеальном случае равно нулю. В качестве примера на рис. 1.2 штриховой линией показана амплитудно-частотная характеристика идеального фильтра нижних частот с единственной полосой пропускания 0 < ω < ωс и полосой задерживания, ω > ω1. Частота ωс между двумя этими полосами определяется как частота среза.
относительно велико, а в идеальном случае постоянно. Диапазоны частот, в которых сигналы подавляются, образуют полосы задерживания и в них значение амплитудно-частотной характеристики относительно мало, а в идеальном случае равно нулю. В качестве примера на рис. 1.2 штриховой линией показана амплитудно-частотная характеристика идеального фильтра нижних частот с единственной полосой пропускания 0 < ω < ωс и полосой задерживания, ω > ω1. Частота ωс между двумя этими полосами определяется как частота среза.
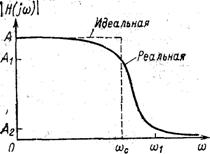
Рис. 1.2. Идеальная и реальная амплитудно-частотные характеристики фильтра нижних частот
В качестве полосы пропускания выбирается диапазон частот, где значение амплитудно-частотной характеристики превышает некоторое заранее выбранное число, обозначенное А1 на рис. 1.2, а полосу задерживания образует диапазон частот, в котором амплитудно-частотная характеристика меньше определенного значения, например, А2. Интервал частот, в котором характеристика постоянно спадает, переходя от полосы пропускания к полосе задержания, называется переходной областью ωс < ω < ω1.
Значение амплитудно-частотной характеристики можно также выразить в децибелах (дБ) следующим образом:
![]()
и в этом случае a характеризует затухание.
В основном затухание в полосе пропускания никогда не превышает 3 дБ.
1.2 Передаточные функции
Невозможно создать идеальные фильтры, но с помощью реализуемых фильтров (которые разрабатываются на основе реальных схемных элементов) можно получить приближения к идеальным. Передаточная функция реализуемого фильтра представляет собой отношение полиномов:
![]()
Коэффициенты а и b – вещественные постоянные величины, a m, n=1, 2, 3… (m £ n).
Степень полинома знаменателя n определяет порядок фильтра. Реальные амплитудно-частотные характеристики лучше (более близки к идеальным) для фильтров более высокого порядка. Однако повышение порядка связано с усложнением схем и более высокой стоимостью. Таким образом, один из аспектов разработки фильтров связан с получением реализуемой характеристики, аппроксимирующей с некоторой заданной степенью точности идеальную характеристику при наименьших затратах.
Похожие работы
... Сравнительная характеристика различных реализаций синтезируемого фильтра. 17 Литература..................................................................................................................................................................... 18 Задание 1. Представить данные на синтез частотно-избирательного фильтра в графической форме с использованием нормированной ...
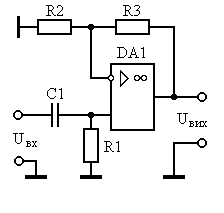
... соединения ФНЧ- ІІ, как на рис. 2.2: Рисунок 2.2 – Структурная схема графа Мезона Выбор схемного решения Схемным решением для данного устройства будет фильтр низкой частоты второго порядка с многопетлевой обратной связью, т.к. он обеспечивает небольшую чувствительность к отклонению номиналов элементов. Используем 3 таких звена, соединённых последовательно. Рисунок 2.3 – ФНЧ-ІІ с ...
... случае a характеризует затухание. Например, предположим, что на рис. 2 выбрано A=1, которому соответствует a=0. Тогда если то затухание на частоте wc a1=-20´lg(1/20,5)=10´lg2=3 дБ. активный полосовой фильтр частотный В основном пропускание в полосе пропускания никогда не превышает 3 дБ. Таким образом, из приведенного примера следует, что значение АЧХ в полосе пропускания ...
... (активные компоненты), но в них нет катушек индуктивности. В дальнейшем активные фильтры почти полностью заменили пассивные. Сейчас пассивные фильтры применяются только на высоких частотах (выше 1МГц), за пределами частотного диапазона большинства ОУ широкого применения. Сейчас во многих случаях аналоговые фильтры заменяются цифровыми. Работа цифровых фильтров обеспечивается, в основном ...

0 комментариев