Навигация
Радиоматериалы и радиокомпоненты
Министерство общего и профессионального образования Российской Федерации
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ
(ТУСУР)
Кафедра КУДР
РЕФЕРАТ
Проверил
Преподаватель кафедры КУДР
__________Кистенева
«___» сентября 2001 г.
Выполнил
студент группы 49В
__________Попов С. В.
«___» сентября 2001 г.
г. Томск
2001 г.
Содержание
1. Металлы.. 3
1.1 Зонная энергетическая структура металлов. 3
1.2 Основные электрические параметры металлов. 5
1.3 удельное сопротивление чистых металлов. 6
1.4 Электрические свойства металлических сплавов. 8
2. Диэлектрики. 10
2.1 Функции, выполняемые диэлектриками в РЭА.. 10
2.2 Виды поляризаций. 10
2.3 Диэлектрические потери. 12
3. Магнитные материалы. 14
3.1. Классификация веществ по магнитным свойствам.. 14
3.2. Классификация магнитных материалов. 15
3.3 Ферриты.. 15
3.3.1 Особенности ферримагнетиков. 16
3.4 Природа обменного взаимодействия. 17
3.5 зависимость магнитных свойств от температуры.. 19
Список литературы.. 21
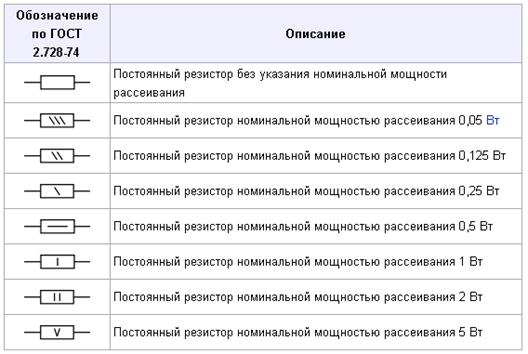
1. Металлы 1.1 Зонная энергетическая структура металлов
Чтобы понять, почему металлы обладают значительной проводимостью, намного большей, чем проводимость диэлектриков и полупроводников, следует рассмотреть какова структура их энергетических зон.
В изолированном атоме имеется ряд разрешённых уровней энергии, которые могут быть «заселены» электронами (рис. 1.1, а). Если атомов много, но они удалены на достаточно большие расстояния друг от друга, структура энергетических уровней не изменяется, а электроны по-прежнему оказываются локализованными вблизи своих ядер. При конденсации вещества и при образовании кристаллической решётки твёрдого тела все имеющиеся у атомов данного типа электронные уровни (как заполненные электронами, так и незаполненные) несколько смещаются вследствие воздействия соседних атомов друг на друга. В частности, притяжение электронов одного атома ядром соседнего снижет высоту потенциального барьера, разделяющего электроны в уединённых атомах. Главное состоит в том, что при сближении атомов происходит перекрытие электронных оболочек, а это в свою очередь существенно изменяет характер движения электронов. Благодаря перекрытию оболочек электроны могут без изменения энергии посредством обмена переходить от одного атома к другому, то есть перемещаться по кристаллу. Обменное взаимодействие имеет чисто квантовую природу и является следствием неразличимости электронов. В этом случае уже нельзя говорить о принадлежности того или иного электрона определённому атому – каждый валентный электрон всем атомам кристаллической решётки одновременно. Иными словами, при перекрытии электронных оболочек происходит обобществление электронов.
Вследствие обменного взаимодействия дискретные энергетические уровни изолированного атома расщепляются в энергетические зоны (рисунок 1.1, б). Разрешенные энергетические зоны разделены запрещёнными интервалами энергии (запрещёнными зонами - ЗЗ). Уровни энергии внутренних оболочек, которые локализованы вблизи ядра и не подвержены сильному возмущению со стороны окружающих атомов, расщепляются меньше, чем уровни валентных (внешних) электронов.
![]()
![]()
![]()
![]()
![]()
![]() Уровни возбуждённого атома
Уровни возбуждённого атома
![]()
![]()
![]()
![]() ЗП
ЗП
![]()
ЗЗ
![]()
![]()
![]()
![]()
![]() ВЗ
ВЗ
![]()
Уровень невозбуждённого состояния атома
а) б)
Рисунок 1.1 – энергетические уровни:
а – уединённого атома;
б – твёрдого тела;
Рассмотрим простую кристаллическую решётку, образованную одним сортом атомов. В каждой разрешённой энергетической зоне содержится столько уровней энергии, сколько атомов содержится во всём кристалле. Если учесть, что энергетические зоны имеют ширину порядка единиц эВ, то для кристалла размером 1см3, содержащего 1022-1023 атомов, энергетическое «расстояние» между уровнями окажется ~ 10-22-10-23 эВ. Эти цифры говорят о том, что энергетический спектр зоны можно считать непрерывным, поскольку даже тепловые флуктуации энергии электрона при нормальных условиях составляют значительно большую величину ~ 103эВ.
Стремление системы атомов к минимуму энергии приводит к тому, что энергетические уровни зон заселяются имеющимися электронами «снизу - вверх». При этом действует принцип Паули – каждый уровень может быть заселён не более чем двумя электронами. В итоге, нижние (внутренние) зоны заселяются полностью вплоть до зоны, образованной валентными уровнями. Валентная зона (ВЗ) является последней заселяемой зоной. В зависимости от «укомплектованности» электронами она может оказаться либо полностью заполненной, либо частично заполненной. Например, если валентная зона образована S-оболочками атомов, имеющих по одному электрону (щелочные металлы), то она будет заполнена ровно на половину. Следующая за валентной зоной свободная, незаполненная электронами зона называется зоной проводимости (ЗП). Взаимное положение этих зон и степень заполнения валентной зоны определяют большинство процессов, происходящих в твёрдом теле.
1. Предположим, что валентная зона заселена полностью (рисунок 1.2). Если при этом между валентной зоной и зоной проводимости имеется достаточно большая зона запрещённых энергий DЕ > ~ 0.1 эВ, то такое состояние соответствует либо полупроводнику (DЕ < ~ 3 эВ), либо диэлектрику (DЕ > ~ 3 эВ). Находясь в валентной зоне, электроны совершают квантовомеханические движения, но не способны к направленному движению (дрейфу) в электрическом поле, поскольку для этого им необходимо изменять свою энергию, переходя с уровня на уровень. Но уровни в пределах валентной зоны полностью заселены, поэтому дрейф возможен лишь при условии перебрасывания части электронов из валентной зоны в зону проводимости за счёт внешних возбуждающих факторов (температурный нагрев, освещёние и т.д.).
Уровни возбуждённого атома
 |  |  | |||
![]()
|
DЕ![]()
![]()
![]() 3
3
 |  |  |
2
а) б) в)
1 – валентная зона;
2 – зона проводимости;
3 – запрещённая зона;
Рисунок 1.2 – структура энергетических зон диэлектриков (а),
полупроводников (б) и металлов (в).
2. Случай, когда запретная зона оказывается незначительной, или вообще отсутствует, (валентная зона перекрывается с зоной проводимости) соответствует материалу высокой проводимости – металлы, поскольку электроны получают возможность относительно свободно изменять свою энергию при воздействии внешнего электрического поля, беспрепятственно переходя из зоны в зону.
3. если валентная зона заселена электронами частично то, очевидно, что соответствующий материал обладает металлическими свойствами независимо от взаимного расположения валентной зоны и зоны проводимости.
Случай перекрытых зон и случай частично заполненной валентной зоны с точки зрения электропроводности эквивалентны. Важно отметить, что уровень Ферми металлов располагается в области разрешённых квазинепрерывных энергетических зон, и что концентрацию носителей заряда («свободных» электронов) можно считать почти постоянной по отношению к изменению внешних условий. Это также отличает металлы от полупроводников, у которых количество носителей заряда резко возрастает с ростом температуры.
1.2 Основные электрические параметры металловИз общего курса физики известно, что плотность электрического тока в веществе определяется зарядом q, концентрацией n и дрейфовой (средней направленной) скоростью носителей заряда vдр
j = q n vдр; (1.1)
Дрейфовая скорость определяется как средняя векторная сумма скоростей электронов. Дрейфовую скорость нельзя путать с тепловой скоростью vт, которая равна среднему модулю скорости электронов:
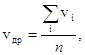
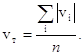 (1.2)
(1.2)
Cсредняя тепловая скорость связана с температурой металла соотношением
mvт2 = 3kT откуда следует, что при комнатной температуре ~ 300К, тепловая скорость значительна и имеет порядок 105 м/с.
В силу того, что направления скоростей электронов хаотичны, в отсутствии электрического поля дрейфовая скорость равна нулю. При воздействии электрического поля электроны получают некоторую добавочную составляющую в направлении поля. Однако эта добавка незначительна, и практически не влияет на характер движения электронов. Элементарные расчёты показывают, что при самом жёстком режиме протекания тока, величина дрейфовой скорости протекания тока составляет не более ~ 10-4 м/с, то есть на 9 и более порядков меньше тепловой. Это связано с тем, что электроны, приобретая от внешнего поля незначительный избыток энергии (сверх тепловой энергии), тут же рассеивают его в материале в результате взаимодействия с динамическими и статическими дефектами. В условиях столь больших сил «терния» имеет место прямая пропорциональность между дрейфовой скоростью и напряжённостью поля:
vдр = m E; (1.3)
Коэффициент пропорциональности m носит название «подвижность» [м2 / В с]. Подстановка (1.3) в (1.1) даёт
j = q n m E; (1.4)
Коэффициент пропорциональности между плотностью тока и напряжённостью поля носит название «удельная проводимость» [g] = [1 / Ом м], а величина, обратная ему – «удельное сопротивление» [r] = [Ом м]:
g = q n m; r = 1/g. (1.5)
1.3 удельное сопротивление чистых металловЕсли бы кристаллическая решётка была бы лишена дефектов, электрическое сопротивление металла равнялось бы нулю, поскольку электроны не испытывали бы рассеяние энергии и беспрепятственно ускорялись в электрическом поле. При этом неподвижные собственные ионы, расположенные в узлах кристаллической решётки не являлись бы рассеивающими центрами, в силу самосогласованности их поле с квантовомеханическим движением электронов.
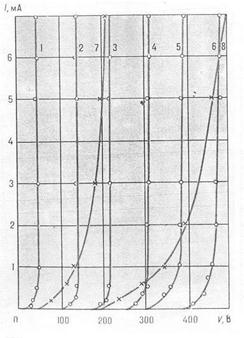
На самом же деле, как отмечалось ранее, присутствие дефектов структуры в кристаллической решётки неизбежно. Рассеяние электронов может произойти и в регулярных частях кристалла, поскольку строгая периодичность его нарушается тепловыми колебаниями ионов. Опыт показывает, что именно тепловые колебания решётки являются главным рассеивающим фактором в чистых металлах. Отсюда следует, что с увеличением температуры сопротивление металлов должно монотонно расти, что и наблюдается в опытах. Рассмотрим типичную зависимость удельного сопротивления чистого металла от температуры (рисунок 1.3, а). Для большинства чистых металлов в области низких температур наблюдается ускоренный рост удельного сопротивления в зависимости от температуры, которую можно описать степенной зависимостью. В области относительно высоких температур, выше так называемой температуры Дебая Тд, зависимость становится близкой к линейной. Характер роста удельного сопротивления на всём диапазоне температур можно объяснить лишь с позиций квантовой теории. Дело в том, что всякое колебание кристаллической решётки можно разложить на элементарные колебания, или колебательные кванты – фотоны. Фотоны, также как и электроны обладают дискретным спектром энергий, причём разрешённая зона фотонов имеет ширину ~ 0.01 эВ. Однако на них не распространяется принцип Паули, и каждому уровню энергии может соответствовать сколь угодно большое число фотонов. Говоря упрощённо, при возрастании температуры от абсолютного нуля до температуры Дебая, увеличивается количество фотонов, соответствующее каждому отдельному возбуждённому уровню энергии. Но, кроме того, возбуждаются всё более и более высокие уровни энергии фотонов. При температуре Дебая возбуждены уже все фотонные уровни, поэтому прирост фотонов замедляется и зависимость r(Т) переходит в линейную. Как показывает эксперимент, линейная аппроксимация температурной зависимости r(Т) справедлива для температур выше 2/3 Тд с ошибкой, не превышающей 10%. Температура Дебая для большинства металлов составляет 400 – 450К, поэтому линейное приближение обычно справедливо для температур от комнатной и выше. Вблизи температуры плавления Тпл происходит отклонение от линейного закона, а при температуре плавления происходит резкий скачёк удельного сопротивления, связанный с фазовым переходом. Как правило, сопротивление сплава выше, чем сопротивление твё1рдого металла. Исключение составляют такие металлы, как Bi, Ga и др, у которых при температуре плавления сопротивление падает.
В области температур, близких к абсолютному нулю, некоторые металлы (например, Nb, Sn, Al, Zn, Hg и др.) переходят в сверхпроводящее состояние, при котором удельное сопротивление резко снижается до нуля (рисунок 1.3, б). У металлов, не переходящих в сверхпроводящее состояние (например, Pt, рисунок 1.3, б), при снижении температуры вплоть до нуля, удельное сопротивление остаётся на некотором постоянном уровне r0. это значение называется остаточным сопротивлением. Очевидно, оно не связано с тепловым рассеянием электронов. Опыт показывает, что r0 пропорционально количеству примесей, а также возрастает при закалке и механических деформациях, следовательно, остаточное сопротивление связанно только с наличием дефектов. Из сказанного следует, что удельное сопротивление металла можно представить в виде суммы тампературозависимой и остаточной (постоянной по отношению к изменению температуры) составляющей.
r = rт + r0. (1.6)

![]()
![]()
![]()
![]()
![]()
![]() Для характеристики влияния температуры на некоторую температурозависимую величину (в ограниченном температурном диапазоне, где её изменение можно считать приблизительно линейным), вводят понятие температурного коэффициента этой величины. r / r273
Для характеристики влияния температуры на некоторую температурозависимую величину (в ограниченном температурном диапазоне, где её изменение можно считать приблизительно линейным), вводят понятие температурного коэффициента этой величины. r / r273
![]()
![]()
![]()
![]() r 0,015
r 0,015
![]() Pt
Pt

![]() 0,010
0,010
![]()
Hg
![]()
![]() 0,005
0,005
![]() rост
rост
Похожие работы
... , которые сегодня можно найти в продаже, практически невозможно. Поэтому приведу лишь таблицы и рисунки с данными некоторых проволочных импортных резисторов. Огнестойки проволочные резисторы серии KNP Резисторы постоянные проволочные. Заменяют собой С5-5, С5-16, С5-16МВ Характеристики: · Высокая рассеиваемая мощность, большая перегрузочная способность · Диапазон рабочих температур: -30…+ ...
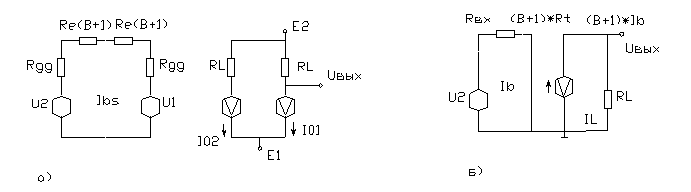
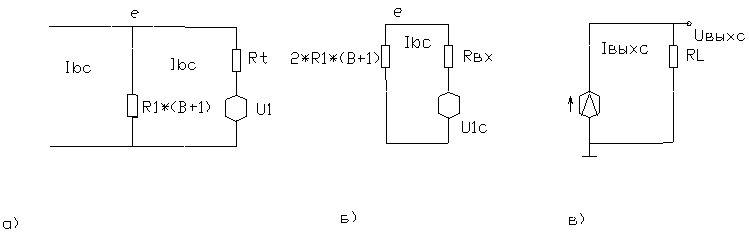
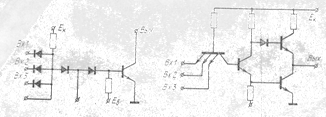
... Uвых2 и Uвых1 можно записать через почти одинаковые коэффициенты усиления К1 и К2 в виде Uвых2 = К2 *U2 , (1) Uвых1 = К1 *U1 . Рис. 1 Парные усилители и квазиидеальный дифференциальный каскад: а) “почти” одинаковые транзисторы Т2 и Т1; б) те же Т2 и Т1 включены в цепь сДК с идеальным генератором тока I0 в эмиттерной цепи (вместе резисторов Ree ...
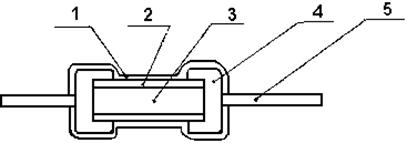
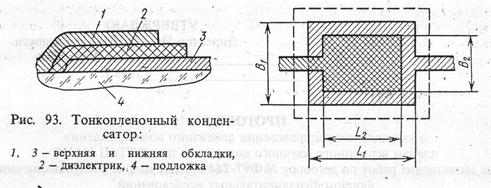
... К22-4 применяют в герметизированных микросхемах вместо конденсаторов К10-9 и К10-17, стоимость которых выше. Размеры этих конденсаторов (2,7¸6,1)´(2,8¸6,8)´2,1 мм. Низкочастотные конденсаторы постоянной емкости В цепях постоянного, пульсирующего и переменного токов низкой частоты в качестве фильтровых, блокировочных и разделительных применяют конденсаторы большой ...
... со стороны планируемого завода-изготовителя, личный опыт и инженерную интуицию. Структура электрической схемы ИС во многом определяется характером выполняемых ею преобразований сигналов. Аналоговое и импульсные схемы выполняют, как правило, точные электрические преобразования, в силу чего их характеристики чувствительны к вариации параметров элементов, к реакции на паразитную обратную связь и ...
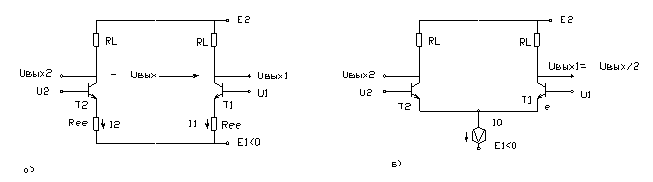
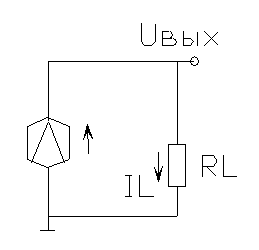
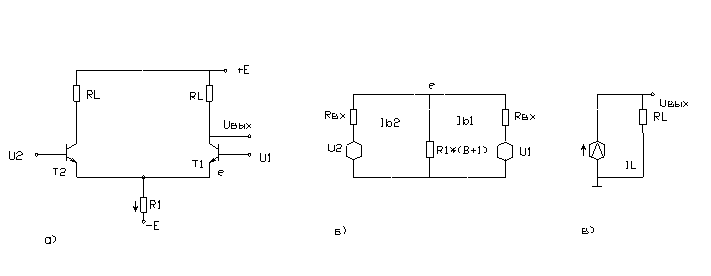
0 комментариев