Навигация
Исследование ФАЛ на толерантность
3.2. Исследование ФАЛ на толерантность.
Определим классы толерантности. Рассмотрим классы толерантности k1, k2, k3, имеющие общие элементы, следовательно, являющиеся пересекающимися множествами.
h1 = h(a1) = h(A) = { X0, X1, X3, X5, X6, X7, X9, X12, X13, X14 }
h2 = h(a2) = h(B) = { X1, X2, X8, X9, X10, X11, X12 }
h3 = h(a3) = h(C) = { X0, X3, X5, X6, X7, X9, X10, X13, X14 }
Проанализировав классы h1, h2, h3, можно получить: k1 Ç k2 = 0;
k1 Ç k3 = 0; k2 Ç k3 = 0, т.е. {k1, k2, k3 } - образуют класс толерантности
Результаты исследования занесем в таблицу 3.
3.3. Исследование ФАЛ на эквивалентность.
Определим классы эквивалентности для этого множества А = {Х0, Х1, ...., Х15 } разобьем на классы эквивалентности, получим 6 классов
М1 = {AC} = {X0,X3,X5,X6 X7,X13,X14}
М2 = {AB} = {X1,X12}
М3 = {B} = {X2,X8,X11}
М4 = { } = {X4,X15}
М5 = {ABC} = {X9}
М6 = {BC} = {X10}
При этом каждый класс полностью определяется любым его представителем. Сопоставив результаты исследования с результатами пункта 3.2 получим следующие зависимости
| М1 Ì K1 | М2 Ì K1 | М3 Ì K2 | М5 Ì K1 | М6 Ì K2 |
| М1 Ì K3 | М2 Ì K2 | М5 Ì K2 | М6 Ì K3 | |
| М5 Ì K3 |
или
K1 = M1 È M2 È M5
K2 = M2 È M3 È M5 È M6
K3 = M1 È M5 È M6
Результаты исследования занесены в таблицу 3. Результаты исследования на эквивалентность и толерантность необходимы для оптимизации построения логической схемы.
3.4. Матрица эквивалентности и толерантности.
Матрицу эквивалентности и толерантности можно представить в виде квадрата, по диагонали которого строятся классы эквивалентности, а затем устраиваются отношения толерантности. Матрица эквивалентности и толерантности представлена в таблице 4.
Матрица эквивалентности и толерантности. Таблица 4.
3.5. Диаграмма Эйлера.
Диаграмма Эйлера дает наглядное представление о том, как распределяются признаки по классам толерантности и эквивалентности. Диаграмма Эйлера для выбранных ФАЛ представлена на рисунке 3.5.
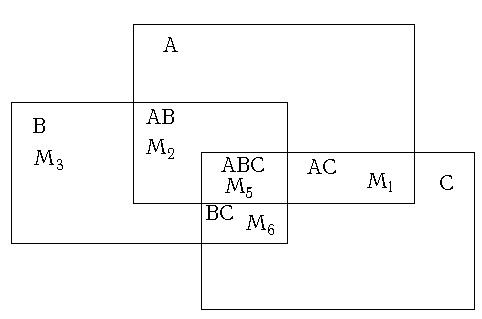
Диаграмма Эйлера. Рис. 3.5
3.6. Построение комбинационной схемы.
Комбинационная схема автомата распознавания набора признаков H = {h1, h3, h5 } построена на основе результатов исследований в пункте 3.1 и пункте 3.4.
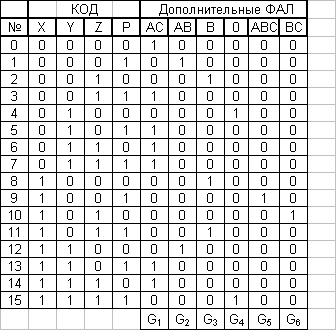
Таблица 5
Используя таблицу 5, можно записать следующие отношения:
G1 = (XYZP) Ú (XYZP) Ú (XYZP) Ú (XYZP) Ú (XYZP) Ú (XYZP) Ú (XYZP) = (XYZP) Ú (XYZP) Ú (XYZP) Ú (XYZ) Ú (YZP)
G2 = (XYZP) Ú (XYZP)
G3 = (XYZP) Ú (XYZP) Ú (XYZP)
G4 = (XYZP) Ú (XYZP)
G5 = (XYZP)
G6 = (XYZP)
Тогда ФАЛ можно представить в виде:
F1 = G1 Ú G2 Ú G5
F3 = G2 Ú G3 Ú G5 Ú G6
F5 = G1 Ú G5 Ú G6
Эти отношения эквивалентны ФАЛ в СДНФ, полученным в пункте 2.5.
Комбинационная схема строилась в два этапа:
1 этап: - построение комбинационной схемы на элементах и, или,
(нестандартных).
2 этап: - замена нестандартных элементов на стандартные и-не
Заключение
Проведя анализ на толерантность и эквивалентность, мы построили автомат, распознающий кортеж признаков H = {h1, h3, h5 }, который состоит из 16 - ти логических элементов.
Список литературы
1. В.П. Сигорский. «Математический аппарат инженера» - издательство Киев: Техника - 1975 г.
Похожие работы
... по соответствующему полю). В окне Конструктора таблиц созданные связи отображаются визуально, их легко изменить, установить новые, удалить (клавиша Del). 1 Многозвенные информационные системы. Модель распределённого приложения БД называется многозвенной и её наиболее простой вариант – трёхзвенное распределённое приложение. Тремя частями такого приложения являются: ...
... характер сигналов интерфейса и их временную диаграмму, а также описание электрофизических параметров сигналов. На рис. 2.2 представлена общая схема сопряжения МП с устройствами ввода-вывода УВВ и ОЗУ в микропроцессорной системе. Рис 2.2. Схема интерфейсных связей микропроцессора Связь МП с УВВ требует пять групп связей, обеспечиваемых через выводы корпуса МП. По группе шин 1 передается ...
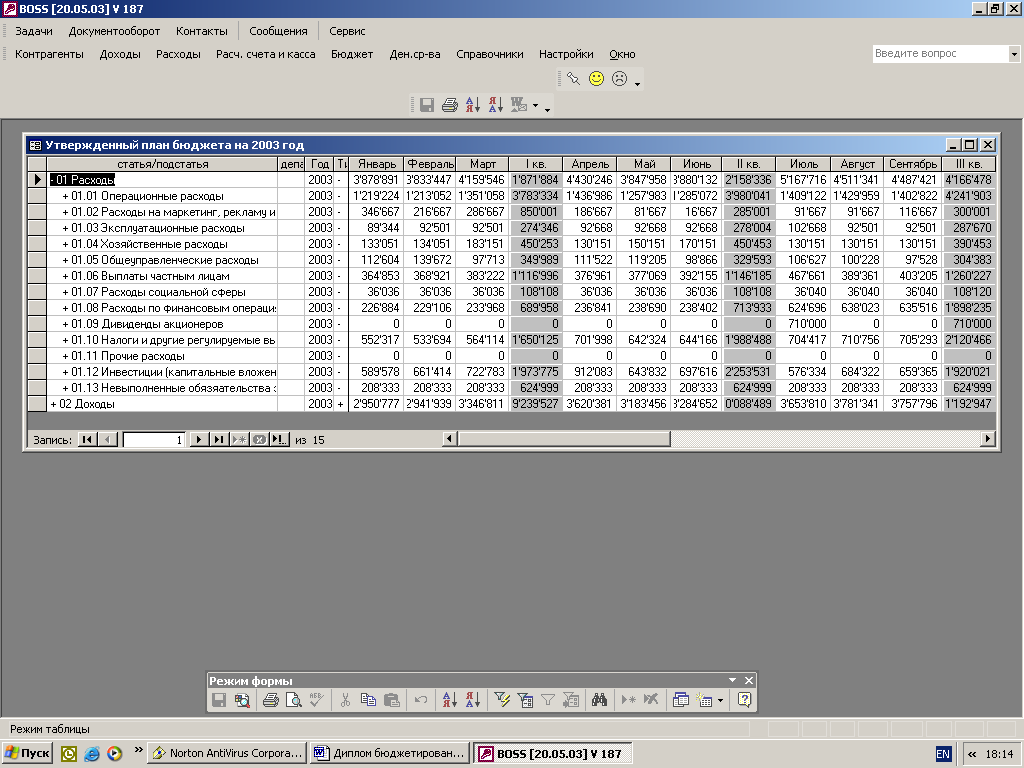
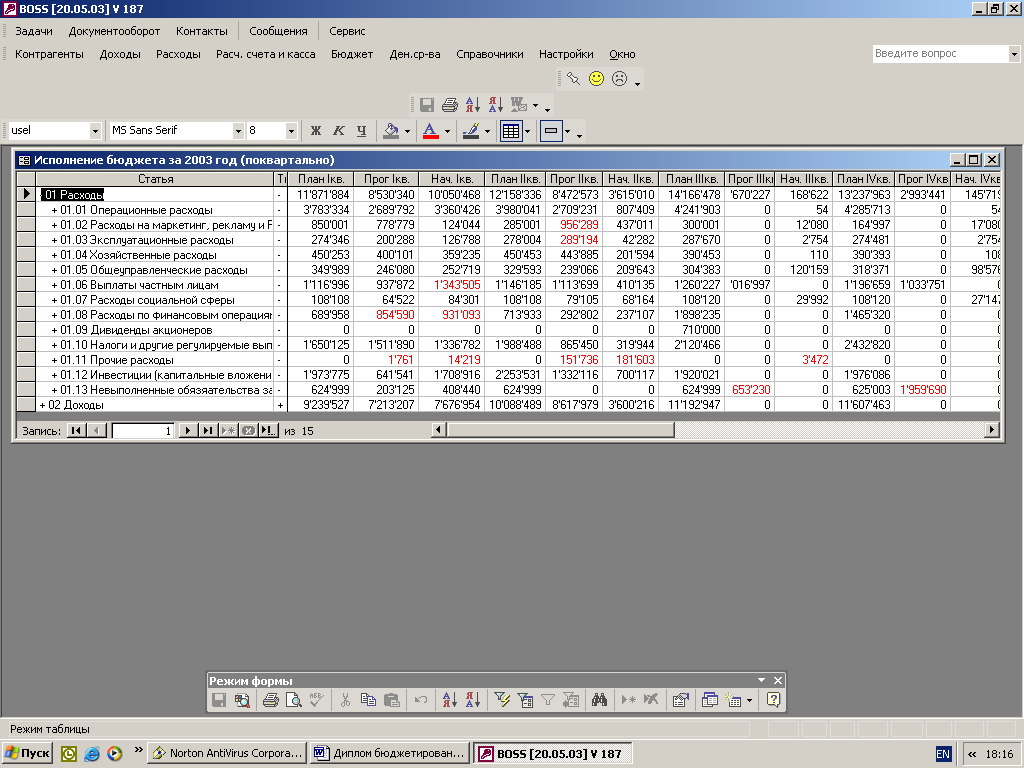
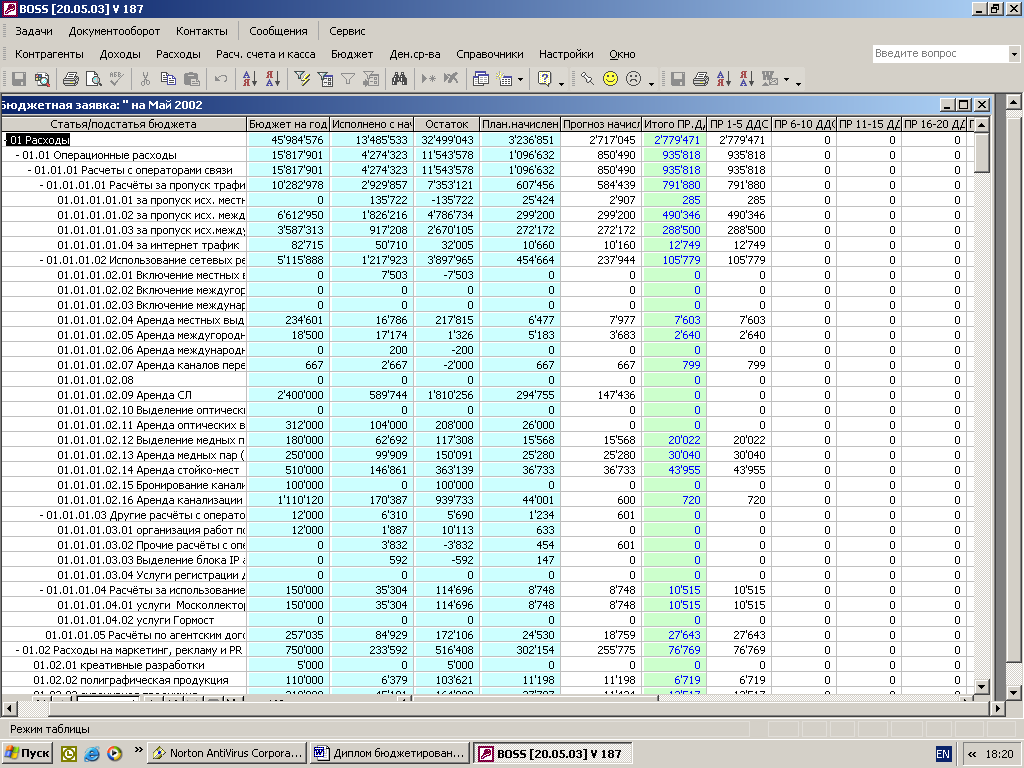
... для реализации системы бюджетирования Консультационной группы "Воронов и Максимов". Статья о проблемах выбора системы бюджетирования - в проекте "УПРАВЛЕНИЕ 3000". Бюджетный автомат Если вы решитесь на автоматизацию системы бюджетирования компании, перед вами сразу встанут вопросы: что выбрать, сколько платить, как внедрять. Примеряйте! О ЧЕМ РЕЧЬ В “Капитале” на стр. 44, 45 мы рассказали ...
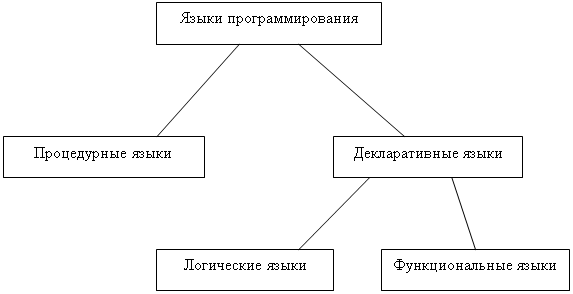
... . В частности: (8) Из (7) и (8) следует, что в M нет двух неравных натуральных чисел. Доказательство закончено. 3.2 Рекурсия Особое место для систем функционального программирования приобретает рекурсия, поскольку она позволяет учитывать значения функции на предыдущих шагах. С теоретической точки зрения рекурсивные определения являются теоретической основой всей современной ...
0 комментариев