Навигация
2.1. Звуковая волна
Мы рассматриваем превращение воздушной массы под воздействием некоторого стороннего источника. Масса воздуха, m в отсутствие управляющего воздействия занимает объем, V и в дальнейшем претерпевает сжатие. Первое состояние единства воздушной массы со средой мы определяем как сохранение занимаемого массой воздуха первоначального объема V. Энергию этого состояния W01 мы определяем как упругую предельную энергию, характерную для объема V:
W01=0.5× k× (D V)2/V, D V® V: W01=× k× V/2
где k, D V — коэффициент объемного сжатия и деформируемая часть объема соответственно.
Энергия возмущения есть кинетическая энергия воздушной массы. Собственную энергию такого возмущения мы определяем при условии свободного перемещения воздушной массы со скоростью, u в объеме V:
W· =m× u 2/2=r × V× u 2/2
где r — плотность воздушной массы. В результате энергетическое пороговое соотношение (3) записывается в виде:
r × V× u 2/2£ k× V/2; u £ u 0, u 0=Ö (k/r )
Мы пришли к известному выражению для скорости звука, u 0.
При выполнении неравенства процесс носит локальный характер: возмущение затухает в объеме V. При достижении скорости звука и далее возникает коллективное возмущение частиц воздушной массы. Это возмущение в виде согласованного колебания частиц свободно проходит через объем V. Заметим, что звуковая волна и нормальные волны на воде не переносят вещества. Они передают возбуждение в пространстве от одной части среды к другой. В то же время солитон Рассела, как мы можем отметить2, осуществляет такой перенос.
2.2. Природа возникновения анизотропного механизма деформирования сыпучего материала.
Рядом авторов в приборе однородного сдвига обнаружена качественная перестройка песчаной среды [4]. Прибор представлял собой камеру 1, установленную в жесткой раме 2 (рис.1). Элементы жесткой рамы служили направляющими при сдвиге камеры. Камера (внутренние размеры 150 ´ 150 ´ 150 мм) была набрана из 30 П-образных пластин 3, изготовленных из оргстекла. Форма пластин позволяла наблюдать кинематику деформирования с трех граней камеры через стекла, которыми закрывались эти грани. Величина сдвига определялась соответствующим поворотом ручек 4 и измерялась по угловой шкале. Объем камеры сохранялся постоянным при любых сдвигах. Так как толщина пластин в 30 раз меньше длины камеры, то при любой деформации сдвига относительное смещение пластин было незначительным (до 2 мм при Г < 20° ). Последнее исключало трение материала о стенки камеры, а также обеспечивало достаточную однородность всех граничных условий. Очевидно также то, что для однородности процессов в плоскости сдвига необходимо, чтобы сила тяжести была направлена к ней по нормали.
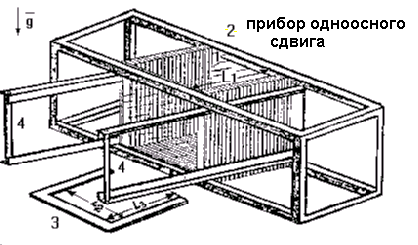
Рис. 1
Материал засыпался в камеру различными способами так, чтобы образец был первоначально однородным и изотропным.
Для малых углов сдвига Г ![]() Г* — некоторый граничный угол, поворот боковых стенок прибора приводит к плавной перестройке структуры образца. При достижении угла Г* + о (Г*) скачком возникает новая фаза эволюции песчаной среды. Среда разбивается на элементы с помощью линий скольжения. В мокром песке образуются трещины. В дальнейшем, когда Г > Г*, деформация сосредоточивается на границах элементов.
Г* — некоторый граничный угол, поворот боковых стенок прибора приводит к плавной перестройке структуры образца. При достижении угла Г* + о (Г*) скачком возникает новая фаза эволюции песчаной среды. Среда разбивается на элементы с помощью линий скольжения. В мокром песке образуются трещины. В дальнейшем, когда Г > Г*, деформация сосредоточивается на границах элементов.
Объясним природу возникающего анизотропного механизма деформирования среды и получим аналитическое решение для граничного угла Г*. Под основным состоянием образца мы будем понимать состояние единства и целостности образующей его песчаной cреды. Такое устойчивое состояние возникает как результат взаимодействия элементов песчаной среды в поле силы тяжести.
Определим энергию Wо1, характеризующую основное состояние образца. Энергию Wо1 мы принимаем равной абсолютной величине работы, затраченной на образование песчаной среды массой m с центром тяжести на высоте h относительно основания прибора как начала отсчета в поле центральной силы тяжести:
![]() (8)
(8)
где r — удельный вес песка; Li (i = ![]() ) — соответствующие размеры рабочей камеры прибора при Г = 0; g — ускорение свободного падения.
) — соответствующие размеры рабочей камеры прибора при Г = 0; g — ускорение свободного падения.
Нетрудно заметить, что одновременно с поворотом боковых стенок начинается возмущение основного состояния образца. Возникающее в образце возмущение (перестройка его структуры) приводит в конечном счете к разрушению его основного состояния.
Очевидно, что для первой фазы эволюции энергия возмущения основного состояния образца W1 не должна превышать энергию, характерную для этого состояния:
W1 ![]() Wо1. (9)
Wо1. (9)
Для случая, когда элементы cреды относительно неподвижны, в среде происходит накопление упругой энергии за счет сжатия с помощью одной из стенок прибора:
![]() , (10)
, (10)
где V — первоначальный объем песка при Г = 0; D V — величина, на которую уменьшается объем V при Г ¹ 0; c — коэффициент, характеризующий механические свойства песка, например предел упругости. Упругая энергия W* рассматривается нами в качестве непосредственного источника возникающего в образце в общем случае возмущения. В соответствии с законом сохранения энергии мы может записать
W* = W1. (11)
С учетом (4) получаем в окончательном виде
W* ![]() Wо1, W*/Wо1
Wо1, W*/Wо1 ![]() 1, (12)
1, (12)
где W* , Wo1 определены в (8), (10).
Граничный угол Г* следует из равенства правой и левой частей соотношения (12):
![]() (13)
(13)
Рассматривая случай, приведенный в [2]: L1 = L2 = L3 = 150 мм — и принимая величины: c = 2 ´ 104 кГ/м2 [4], r = 1,7 ´ 103 кГ/м3 , — можно найти угол ![]() » 9о, близкий по величине к определенному в [2] экспериментально
» 9о, близкий по величине к определенному в [2] экспериментально ![]() = 12о.
= 12о.
На рис. 2 приведены результаты эксперимента для двух видов предварительного уплотнения мокрого песка. Начальные точки теоретических кривых были взяты из эксперимента для определения отношения r /c . Нетрудно отметить согласие между экспериментом и теорией.
Таким образом, мы можем сделать следующий вывод об устойчивости песчаной среды. Устойчивость песчаной среды в рассматриваемом образце к сдвигу в диапазоне 0 < Г < Г* означает способность образца сохранять в этом диапазоне состояние единства и целостности образующей его среды — основное состояние образца на первой фазе его эволюции.
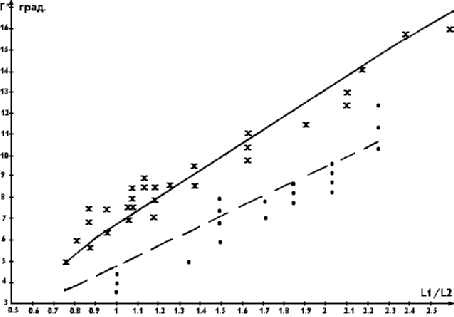
Рис. 2.
Эта способность сохраняется при условии (12), что характеризующая возмущение образца упругая энергия W* не превышает гравитационной энергий Wо1, характеризующей его основное состояние. Нарушение энергетического порогового соотношения (12) приводит к смене основного состояния образца и, как следствие, к качественно новому поведению песчаной среды.
Весьма актуальной представляется попытка [3] распространить проведенное исследование на объяснение природы землетрясений, в частности, наиболее опасных, очаг которых находится в пределах земной коры. Соответствующие линейные размеры Li (i = ![]() ) могли бы характеризовать в этом случае земной блок в иерархии дискретных масштабов [4]. С благодарностью вспоминаю академика М. А. Садовского, обратившего мое внимание на эту задачу в связи с проблемой землетрясения и нашедшего в себе силы обсуждать ее решение перед своим уходом из этой жизни.
) могли бы характеризовать в этом случае земной блок в иерархии дискретных масштабов [4]. С благодарностью вспоминаю академика М. А. Садовского, обратившего мое внимание на эту задачу в связи с проблемой землетрясения и нашедшего в себе силы обсуждать ее решение перед своим уходом из этой жизни.
Известно, что поток частиц может принимать качественно различающиеся состояния, начиная от малоподвижного (потенциального) и кончая потоком с крупномасштабной турбулентностью (хаотичностью движения частиц). Эти превращения характеризуются так называемыми критическими числами Рейнольдса:
Rej = u jr r/h = nj , j = 1,2,3,... ,
где u j, r , r, h — скорость, плотность, линейный размер и динамическая вязкость (динамическое трение) соответственно; nj — некоторое число. Числа Rеj (как и числа Фруда) — известные коэффициенты подобия — входят в состав соответствующих математических моделей в качестве безразмерных параметров управления [4]. Природа этих чисел и, следовательно, природа превращений в потоке частиц была неизвестна до настоящего времени. Покажем, что превращения в потоке частиц есть конкретное проявление закона сохранения и превращения энергии определенного вида. Для этого выделим первые критические числа j = ![]() , отыскивая соответствующие энергетические пороговые соотношения (3). Мы будем использовать известные законы динамического трения в строгом соответствии с определенными участками шкалы возрастающих чисел Re.
, отыскивая соответствующие энергетические пороговые соотношения (3). Мы будем использовать известные законы динамического трения в строгом соответствии с определенными участками шкалы возрастающих чисел Re.
Переход от потенциального потока к сплошному Re1. Потенциальный поток, или “сухая вода” [5], — среда относительно неподвижных и независимых частиц, точнее частиц, совершающих колебания относительно некоторых центральных положений. В качестве основного состояния частицы рассматриваем состояние ее единства с локальной областью среды. Энергию Wо1 , характерную для такого состояния, определяем с использованием закона Стокса
F = 6p h ru
как абсолютную величину работы, затраченной на образование частицы в локальной области среды:
![]() .
.
Собственную энергию возмущения частицы записываем как ее кинетическую энергию, определяя скорость u для ее свободного состояния:
![]() .
.
В результате мы можем записать соотношение между энергиями W* и Wo1 в виде
Re = u r r/h ![]() 4,5 , u 1 = 4,5 h /(r r) , Re1 = 4,5.
4,5 , u 1 = 4,5 h /(r r) , Re1 = 4,5.
Здесь параметры m, r , r, h , u относятся к частице, в частности r — ее радиус. В случае Re > Re1 частица теряет “жесткую” связь со средой; ее кинетическая энергия позволяет преодолеть предел текучести, характеризуемый энергией Wo1; поток переходит из состояния потенциального в состояние сплошного, напоминающего мед [5]. На этой фазе начинается подготовка к расслоению потока, а сама фаза есть катастрофа предыдущей.
Переход от сплошного потока к ламинарному Re2 . В качестве объекта рассматриваем некоторый слой потока с площадью соприкосновения A и линейным поперечным размером r. Основное состояние слоя — состояние его единства со сплошным потоком. Энергию такого состояния определяем как абсолютную величину работы, затраченной на образование слоя в поле квазиупругой силы [5]:
F = Ah u /r
и принимаем равной:
![]()
Началом отсчета для возникающего возмущения на этой фазе является скорость u 1 из-за катастрофы предыдущей связи. Поэтому собственная энергия возмущения слоя записывается в виде
![]()
Предельную скорость u 2 отыскиваем из равенства W*(u — u 1) = = Wo2 . В результате получаем:
u 2 = 7,18 h /r r ,Re2 = 7,18.
В момент, определяемый Re = Re2 , одновременно существуют целостный поток и независимый слой как часть этого потока. Для Re > Re2 начинается расслоение потока в виде скачкообразного выделения слоев с различающейся скоростью; возникает ротор скорости, определяющий в дальнейшем появление мелкомасштабных вихрей. Возникшая фаза есть катастрофа предыдущей.
Переход от ламинарного потока к потоку со стационарными завихрениями Re3. В качестве объекта рассматриваем трубку тока. На основании закона Хагена — Пуайзеля [6] энергию основного состояния мы можем записать в виде
Wo3 = 4p rlu ,
где r, l — радиус трубки тока и ее длина соответственно. Началом отсчета для возникающего возмущения ввиду новой связи является скорость u 2. Собственную энергию возмущения записываем в виде
W*(u – u 2) = p r2lr (u – u 2)2.
Значения Re3 и u 3 находим из равенства W* (u – u 2) = W03:
u 3 = 19,8 h /r r, Re3 = 19,8.
При нарушении энергетического порогового соотношения Re > Re3 перепад давления в трубке исчезает за счет ее закручивания. Возникают стационарные вихри с фиксированными центрами вращения. В свою очередь, на этой фазе происходит катастрофа — смена геометрического образа потока. Начинается подготовка к отрыву образовавшихся вихрей от локальных центров вращения.
Образование вихревой цепочки Кармана Re4 . Энергия основного состояния потока, формирующая цилиндрическое вихревое образование, записывается на основании известного закона для момента сил [5]:
![]() ,
,
— и равна:
Wo4 = 4p 2h lru .
Собственная кинетическая энергия вращающегося цилиндра равна:
![]()
где r, l — радиус и длина цилиндра соответственно. Из предельного равенства W* = Wo4 находим
u 4 = 43,06 h /r r , Re4 = 43,06.
В момент Re = Re4 вихрь есть одновременно часть локальной области и движущегося потока. При переходе Re > Re4 вихри отрываются от центров вращения и становятся частью потока.
Найденные числа Rej, j = ![]() , являются конкретным выражением исследуемого нами закона и находятся в согласии с соответствующими участками диапазона Re, указанными в [5].
, являются конкретным выражением исследуемого нами закона и находятся в согласии с соответствующими участками диапазона Re, указанными в [5].
Фазируемые антенные решетки (ФАР) являются антеннами, принимающими и излучающими электромагнитные волны сверхвысоких частот (СВЧ), и представляют собой определенное множество элементарных излучателей (элементов), объединенных в одно целое с помощью системы СВЧ питания таким образом, что формируемый ФАР электромагнитный луч может перемещаться в свободном пространстве за доли секунды, обслуживая практически полусферу.
Отмечен [5] эффект исчезновения луча под определенными угловыми направлениями для некоторых конструкций ФАР. Эффект получил название “слепые пятна” ФАР и весьма нежелателен для радиолокации, где применяются сами ФАР.
В антенне возникает явление резонанса, когда СВЧ электромагнитная энергия отражается от апертуры к генератору волн. Для возникающей аномалии характерно, что в диаграмме направленности элемента в составе решетки возникают нулевые провалы под соответствующими “слепым пятнам” углами. В то же время для одиночного излучателя таких провалов нет. Природа эффекта считалась неизвестной.
Соответствующее энергетическое пороговое соотношение было получено нами ранее [8]:
![]()
где l — длина волны в свободном пространстве; j — азимут; q — угол, отсчитываемый от нормали к апертуре ФАР. Здесь параметр gи представляет собой относительную мощность, излучаемую синфазно и равномерно возбужденной площадкой S, приходящейся на один элемент в апертуре решетки, под углами q , j . Параметр gи характеризует основное состояние элемента.
Параметр g0 представляет собой относительную мощность, излучаемую одиночным элементом в токопроводящем экране под q , j , и характеризует собственную энергию возмущения элемента в составе решетки. Соотношение было апробировано с помощью результатов физического и вычислительного экспериментов, приведенных в известной литературе или полученных автором.
Удовлетворение неравенства определяет случай слабого взаимодействия излучателей в решетке: gэ » g0 , gэ — относительная мощность, излучаемая в направлении q , j элементом в составе решетки. В то же время нарушение этого неравенства в рассмотренных случаях приводило к появлению качественно нового типа электромагнитного поля и, как следствие, к появлению нулевых провалов в диаграмме направленности gэ (q , j ).Следует заметить также, что соотношение g0/gи выполняет роль коэффициента подобия для ФАР аналогично числам Re , Фr.
Благодарен М. М. Ганцевичу за полезное обсуждение по теме раздела и постоянные призывы к простоте изложения.
2.5. Скачки в поле упругих сил: машина Зимана.Система [6] представляет собой плоский диск 3 с двумя пружинками (или резинками) и размещается на плоскости YOX (рис. 3). Диск может поворачиваться вокруг своей оси с центром в точке О1; концы пружинок 1, 2 размещены подвижным образом на периферии диска в точке а; второй конец пружинки 1 закреплен также подвижно на плоскости в точке F. Возмущение в систему вносит перемещение свободного конца пружинки 2 с координатами x, y.
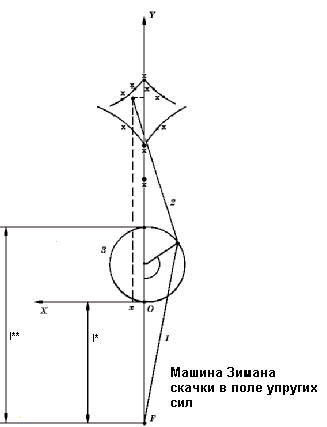
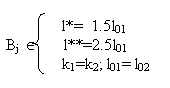
Рис. 3
Машина Зимана была предложена ее автором в качестве модели в связи с исследованиями в области теоретической биологии, например, с анализом развития костных или мышечных тканей из одной и той же клеточной культуры. Известна ромбовидная область, определенная своими границами Bj , j = ![]() , где перемещение свободного конца c пружины 2 приводит к плавному изменению геометрии машины. Соответствующее пересечение границ области концом c вызывает скачок в состоянии системы. В частности, пересечение нижнего вертикального клюва y2 приводит к началу плавного вращения диска. В то же время приход в точку верхнего вертикального клюва y3 делает диск неподвижным при дальнейшем движении c вдоль оси Y. При пересечении концом c боковой границы, например в случае B4 (90°
, где перемещение свободного конца c пружины 2 приводит к плавному изменению геометрии машины. Соответствующее пересечение границ области концом c вызывает скачок в состоянии системы. В частности, пересечение нижнего вертикального клюва y2 приводит к началу плавного вращения диска. В то же время приход в точку верхнего вертикального клюва y3 делает диск неподвижным при дальнейшем движении c вдоль оси Y. При пересечении концом c боковой границы, например в случае B4 (90° ![]() q
q ![]() 180° ), следует бросок диска из области q < 180° в область q > 180° .
180° ), следует бросок диска из области q < 180° в область q > 180° .
Выделим в рамках закона сохранения и превращения энергии определенного вида бифуркационное множество Bj. Прежде определим особые точки на вертикальной оси yj , j = ![]() . Собственную энергию возмущения машины мы определяем как упругую энергию пружины 2, исключая из рассмотрения связь диска с плоскостью через посредство пружины 1. Мы сохраняем при этом все остальные физические и геометрические условия, ограничения, совокупность которых образует машину Зимана, и определяет в ней физические процессы. Очевидно, что этому отвечает случай нахождения точки a в крайнем нижнем положении q = 0 и перемещения конца c вдоль оси Y: х = 0. Для энергии
. Собственную энергию возмущения машины мы определяем как упругую энергию пружины 2, исключая из рассмотрения связь диска с плоскостью через посредство пружины 1. Мы сохраняем при этом все остальные физические и геометрические условия, ограничения, совокупность которых образует машину Зимана, и определяет в ней физические процессы. Очевидно, что этому отвечает случай нахождения точки a в крайнем нижнем положении q = 0 и перемещения конца c вдоль оси Y: х = 0. Для энергии ![]() мы можем записать в результате
мы можем записать в результате
![]()
где к2 — коэффициент упругости пружины 2; y = l2 — длина пружины при с = с(0, y); l02 — длина пружины 2 в спокойном состоянии. Первое основное состояние диска мы определяем как состояние его “жесткой” связи с плоскостью. Энергию этого состояния записываем в виде
![]()
где к1 — коэффициент упругости пружины 1; l* — длина пружины 1 при q = 0о ; l01 — длина пружины 1 в спокойном состоянии. Второе основное состояние определяем как состояние связи точки а с центром вращения диска о1. Энергию, характеризующую это состояние, мы определяем как абсолютную величину работы, затраченной на перемещение точки а из центра о1 как начала отсчета на периферию диска x = 0, y = 0 в поле упругой силы пружины 2:
![]() ,
,
где r — радиус диска. Третье основное состояние — состояние связи точки а с точкой x = 0, y = l** на плоскости. Соответствующую энергию Wo3 мы определяем как энергию собственно перехода точки а из положения x = 0, y = 0 в крайнее верхнее положение x = 0, y = l** в поле упругой силы пружины 1. Учитывая, что возникающие скачки вызывают смену связи диска с плоскостью, мы можем соответствующие энергетические пороговые соотношения записать в виде:
W*![]() ;
;
W*![]() ;
;
W*![]()
откуда особые точки на вертикальной оси равны:
![]()
Для случая к1 = к2; l01 = l02; l* = 1,5l01; l** = 2,5l01, описанного в [9], имеем: y2 = 2l01, y3 = 3l01, что близко к значениям: y2 » 1,9l01, y3 » » 2, 96l01 , полученным в этой работе с помощью математической модели.
В то же время полученные нами решения, в отличие от представления [9], соответствуют общему случаю задания параметров к1,2; l*; l** . Преодоление y > y1 на вертикальной оси приводит к появлению чувствительности точки а к горизонтальным перемещениям конца с пружины 2. Преодоление точки x = 0, y = y2 приводит к началу вращения диска при малом отклонении конца с от вертикальной оси и его последующем движении вдоль этой оси: q = q (y) .
Окончательно границы Bj определяем, рассматривая движение конца с параллельно оси X: с = с (x — var, y — const). Собственную энергию возмущения определяем как энергию деформации x пружины 2, расположив эту пружину параллельно оси Х из точки а:
![]()
Энергия основного состояния в этом случае представляет собой упругую энергию, накопленную пружиной 1 при перемещении точки а из положения q = 0о в положение q :
ì (l1 – l*)2 , q £ 90о;
Wо1 = (к1/2) ´ í
î (l** – l1)2 , q ³ 90о.
В результате мы можем записать соответствующее энергетическое пороговое соотношение, дополнив его для определения необходимых параметров еще тремя уравнениями:
![]() ; (13б)
; (13б)
![]() ; (13в)
; (13в)
![]() . (13г)
. (13г)
Здесь уравнения (13б), (13в) получены из геометрии машины (рис. 4), уравнение (13г) представляет запись закона сохранения энергии, адекватную фазе вращающегося диска: y > y2 . Задавая численные значения одного из параметров: x, y, l1 , l2 , q , например х, можно остальные параметры определить, решив совместно предельный вариант выражения (13а)
W* = Wо1
и уравнения (13б) — (13г). На рис. 4 приведены рассчитанная по этим формулам граница Bj и ее экспериментальные значения для частного случая. Можно отметить хорошее совпадение теории и эксперимента. Нетрудно также убедиться, что отношения вида
![]() ,
, ![]()
позволят однозначно задать состояния машины на соответствующих фазах ее эволюции, выполнив ту же роль, что и числа Фr , Re , g0/gи, Wy /Wо1 (12).
2.6. Математический маятник. Собственные частоты.Математический маятник имеет длину l и массу m. Точка подвески совершает колебания вдоль вертикальной оси относительно среднего положения по закону х = Asinw t . Имеет место начальное возмущение маятника по горизонтальной оси. Известны [10] две особые частоты w 1,2, которые разграничивают качественно отличающиеся между собой режимы колебаний маятника. В этом случае лишь продемонстрируем, что частоты w 1,2 и связанные с ними события представляют, как и предыдущие случаи, следствие закона сохранения и превращения энергии определенного вида.
К основным состояниям маятника мы можем отнести его принадлежность к крайнему нижнему положению относительно точки подвески и к горизонтальной плоскости, к которой принадлежит это положение. Для первого состояния характерна энергия
Wо1 = mgl/2,
где g — ускорение свободного падения. Энергия Wо1 представляет собой работу, совершенную при выходе массы m из точки подвески как начала отсчета в поле центральной силы тяжести в крайнее нижнее положение. Для второго состояния характерна энергия выхода тела с эквипотенциального уровня, определяемого расстоянием l относительно точки подвески:
Wо2 = mgl.
Энергия возмущения маятника характеризует его колебания. Собственную энергию колебаний маятника с частотой w определяем, исключая взаимодействие материальной точки с массой m и подвески. В этом случае мы рассматриваем маятник, включающий в себя точку подвески, нить, материальную точку, как одно целое: A = l . Собственную энергию W* мы записываем как полную энергию осциллятора:
W* = mw 2A2/2.
В результате следуют два пороговых соотношения:
![]() ;
;
![]()
Первое соотношение определяет порог чувствительности материальной точки к колебаниям подвески. Режим накачки (резонанс) при w = w 1 переходит в режим вынужденных колебаний при w > w 1, где материальная точка и подвеска образуют одно целое. Второе энергетическое пороговое соотношение разграничивает фазу колебаний маятника относительно крайнего нижнего положения как устойчивого (аттрактора) и фазу колебаний с устойчивым положением, постепенно поднимающимся вплоть до вертикального. Соотношения, записанные в виде w 2A2/gl, выполняют роль коэффициентов подобия аналогично числам Рейнольдса, Фруда, а также другим числам, полученным в предыдущих разделах.
2.7. Космические скорости земли.В этом случае продемонстрируем также, что рассматриваемые события есть следствие закона сохранения и превращения энергии определенного вида. Существуют два основных состояния запускаемого с Земли аппарата: для одного из них характерна жесткая связь массы m с Землей, имеющей радиус R. В то же время второе состояние определяет связь тела массой m с поверхностью Земли, т.е. принадлежность тела определенному эквипотенциальному уровню. Для этих состояний характерны энергии:
![]() ;
;
![]() .
.
Энергия Wo1 равна абсолютной величине работы, затраченной на выход тела на поверхность земли из ее центра как начала отсчета в поле центральной силы тяжести. Вторая характерная энергия Wo2 соответствует выходу тела с поверхности Земли как некоторого эквипотенциального уровня. Собственная энергия возмущения тела представляет собой кинетическую энергию, где скорость u определена в отсутствие сопротивления воздуха:
![]()
В результате два пороговых соотношения определяют все многообразие поведения объекта, а реальные граничные скорости u 1,2 соответствуют переходу от одного поведения к другому — качественно новому:
![]() ,
,
![]() .
.
Многочисленные публикации по этой теме посвящены процессу протекания разряда и догадкам об отдельных сторонах его природы. Объясним возникающий феномен в рамках закона сохранения и превращения энергии определенного вида. Электрический разряд представляет собой упорядоченное и направленное движение массы электрически заряженных частиц в некотором объеме V. Между тем любое движение тяжелой массы связано с преодолением силы тяжести. Для основного состояния газа характерно хаотическое неупорядоченное движение — тепловое движение образующих его частиц в пределах свободного пробега. Такое состояние относительной неподвижности частиц газа сложилось в результате силы тяготения. Соответствующая энергия Wo1 записывается нами в знакомом по предыдущим примерам виде:
![]() , (14)
, (14)
где m — масса газа, заключенного в объеме V с характерным линейным размером l и плотностью r ; g — ускорение свободного падения. Возмущение основного состояния газа возникает в результате воздействия на него электромагнитного поля. Собственная энергия возмущения газа определяется нами как энергия электрического поля свободных зарядов в объеме V:
W* = ![]() V,
V,
где Е, e — напряженность электрического поля и абсолютная диэлектрическая проницаемость газа соответственно.
Объединяя энергии W*, Wо1 в энергетическом пороговом соотношении, получаем необходимое и достаточное условие существования газа как диэлектрической среды:
E/Ep £ 1, E £ Ep, Ep = ![]() , e = e ¢ e 0, e 0 = 8,85 ´ 10-12 Ф/м, (15)
, e = e ¢ e 0, e 0 = 8,85 ´ 10-12 Ф/м, (15)
где Ер — напряженность при разряде — разрядная напряженность; e ¢ — относительная диэлектрическая проницаемость. Нарушение соотношения (15) приводит к распаду единой целостной среды, каковой являлся до этого газ. Возникает упорядоченное внешним силовым полем и направленное движение электронов — электрический разряд. Соотношение (15) находится в согласии с экспериментальными данными, известными в [11], в частности зависимость разрядной мощности Рр от давления р (атм):
Рр ~ р, Рр ~ Ер2.
Если учесть, что плотность связана с Р, атм, и температурой T, K, известным выражением
![]() ,
,
то получим из (15) искомую зависимость. Зависимость Ер(l ), где l — длина волны, приведенную в литературе, можно объяснить исходя из зависимости коэффициента преломления n = n(l )=![]() . Легко усмотреть родственность электрического разряда и трещины в геофизической среде (§ 2.3). Действительно, одинаковые правые части Wо1 в выражениях (8), (14) предопределяют одинаковый исход: среда, некогда единая и целостная, разбивается на части. Различие левых частей W* в соответствующих соотношениях приводит к отличным языкам (механизмам) описания (протекания) такого исхода в каждом из рассматриваемых случаев. Можно сказать, что разряд — это электрическая трещина, возникающая в газовой среде. Следующее основное состояние, на которое переключается газ, и соответствующая энергия характеризуют принадлежность данной массы газа определенному эквипотенциальному уровню:
. Легко усмотреть родственность электрического разряда и трещины в геофизической среде (§ 2.3). Действительно, одинаковые правые части Wо1 в выражениях (8), (14) предопределяют одинаковый исход: среда, некогда единая и целостная, разбивается на части. Различие левых частей W* в соответствующих соотношениях приводит к отличным языкам (механизмам) описания (протекания) такого исхода в каждом из рассматриваемых случаев. Можно сказать, что разряд — это электрическая трещина, возникающая в газовой среде. Следующее основное состояние, на которое переключается газ, и соответствующая энергия характеризуют принадлежность данной массы газа определенному эквипотенциальному уровню:
W02 = mgl,
соотношение между W* и Wо2
E £ ![]() Ep
Ep
однозначно определяет вытекающие из этого основного состояния события. Нарушение этого энергетического порогового соотношения приводит к перемещению разряда в пространстве по мере увеличения энергии W*. Газ усваивает возрастающую энергию W* посредством перемещения разряда в область все более высокого эквипотенциального уровня в поле электрической силы, т.е. к источнику электрической энергии. Аналогично предыдущим случаям соотношение вида (15) выполняет роль коэффициента подобия для различных сценариев электрического разряда в газовой среде.
2.9. Электрический аналог звуковой волныЕсли в качестве основного состояния газа принять сохранение постоянным объема, который он занимает, то соответствующая энергия записывается в виде
Wо1 = ![]() KV,
KV,
где K, V — обозначения, приведенные в § 2.2. В результате мы можем переписать соотношение (15) в виде
E/E1 £ 1 , E £ E1 , E1 = ![]() . (16)
. (16)
Связанные с соотношением (16) события еще подлежат идентификации. Однако исходя из аналогии со звуковой волной (основные состояния и соответствующие энергии в обоих случаях одни и те же), можно сделать следующие выводы. Для случая, ограниченного условием (16), возникающие в определенном объеме перемещения электрических зарядов под воздействием электрической силы носят хаотический характер. Существующее сопротивление уменьшению объема, определяемое энергией Wо1 и условием (16) в целом, препятствует распространению возбуждения вне объема. Смена знака неравенства на противоположный приводит к качественно новой ситуации. Сжатие объема сменяется его расширением. Возникает согласованное колебание электрических зарядов, которое распространяется на сопредельные области. Важно отметить две особенности: перенос вещества отсутствует; на этой фазе возникают пространственные области, где должна существенно возрастать плотность электрических зарядов.
2.10. Шаровая молния: природаНазовем последовательность основных состояний и характерных для этих состояний энергий, преодоление которых должно приводить к возникновению феномена. Так же, как игра в снежки требует предварительно уплотнить снег — получить снежок и затем привести его в движение, образование шаровой молнии связано с несколькими основными фазами. Прежде всего должно произойти рождение коллектива организованных с единым возбуждением электрических зарядов. Для этого необходимо, чтобы существовал некоторый порог, позволяющий как плотина определенным образом выровнять и связать воедино состояния отдельных зарядов. Таким порогом может служить основное состояние, для которого характерно сохранение постоянным объема газа. Соответствующее энергетическое пороговое соотношение, в рамках которого происходит подготовка к коллективному возмущению зарядов, имеет вид (16). Преодоление энергетического порога Wо1 (16) приводит к периодически возникающему в объеме V уплотнению электрических зарядов. Периодическое уплотнение сменяется состоянием с постоянным уплотнением электрических зарядов на новой фазе:
Ve (E – E1)2 > PпV ; E2 = ![]() + E1 , (17)
+ E1 , (17)
где Рп — давление, соответствующее пределу упругости среды Е1 из (16). На следующей фазе образовавшийся сгусток электрических зарядов должен освободиться от неподвижности в пространстве:
![]() (18)
(18)
где m, g, r , l определены в § 2.9. И, наконец, преодоление дополнительного порога энергии Wo2 = mgl :
![]() (19)
(19)
позволяет электрическому шару начать перемещение в пространстве. Целью такого перемещения может быть “сброс” электрической энергии в соответствии с теоремой Лагранжа. Например, преобразование этой энергии в тепловую. Соотношения (16) — (19), записанные в виде e Е2/K, e (E – E1)2/Pп, ... выполняют роль управляющих параметров процесса образования шаровой молнии на соответствующих фазах и являются коэффициентами подобия для различных сценариев его протекания на этих фазах.
2.11. Ударная волнаОсновные состояния для газовой и жидкой сред и характерные для этих состояний энергии сохраняются теми же, что и в предыдущем случае. Однако роль управляющего воздействия в этом случае выполняет кинетическая энергия стороннего источника; возмущение представляет собой механическое движение частиц среды. Собственная энергия возмущения записывается, как и в случае звуковой волны (§ . 2.2). Звуковая волна является первой в ряду метаморфоз, которые претерпевает среда частиц при формировании ударной волны. Соответствующее энергетическое пороговое соотношение было приведено ранее. Следуя далее (§ 2.11), мы отмечаем возникновение области со сверхуплотненным веществом, которая затем отрывается от источника и начинает перемещаться со сверхзвуковой скоростью. Совокупность соответствующих энергетических пороговых соотношений приводится нами ниже:
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Действуя аналогично, можно получать выражения для случая твердого тела.
2.12. Реореакция рыб в потоке водыДо сих пор мы рассматривали поведение физических объектов. В таком поведении мы отмечали скачок как результат управляющего воздействия физической природы в согласии с приведенной выше формулировкой закона сохранения и превращения энергии определенного вида. В этом случае покажем, что в согласии с обсуждаемым нами законом может находиться и поведение биологического объекта. Известна граничная скорость потока воды u 1 , разделяющая поведение рыб на два характерных типа [12]. При скоростях u < u 1 рыбы плавают произвольно в пределах участка воды, где они обитают. Превышение пороговой скорости u > u 1 приводит к возникновению нового вида поведения: рыбы ориентируются строго против потока.
В качестве исследуемого объекта в этом примере должна выступать вытесняемая рыбой вода. Именно эта вода непосредственно связывает рыбу с окружающей средой. Основное состояние вытесненной воды характеризует ее связь с рыбой. Соответствующая энергия Wo1 основного состояния записывается нами в виде
![]()
где m, h — масса вытесненной рыбой воды и расстояние между центрами тяжести и объема рыбы соответственно. Возмущение вытесненной воды представляет собой ее поступательное относительно рыбы движение. Собственная энергия такого возмущения записывается нами в виде
![]()
где u — скорость потока воды, идеализированная скорость вытесненной воды.
Когда имеет место соотношение
![]()
существующий баланс сил тяжести и выталкивающей делает для рыб равнозначным с точки зрения энергетических затрат любое направление плавания в пределах постоянного участка (экологи-
ческий факт). Превышение критической скорости u 1 приводит к горизонтальной подвижке вытесненной воды в направлении на поток относительно центра тяжести рыбы. Возникает пара уже названных сил с точками приложения, разнесенными вдоль рыбы. Произвольное плавание рыб в общем случае требует компенсации этого эффекта. В результате энергетически выгодным с учетом сохранения участка обитания становится направление на поток. Интересно, насколько справедлив сделанный вывод в целом, если имеющиеся данные о критических скоростях и геометрии рыб качественно согласуются с ним [13].
III У порога нового мира 3.1. Вселенная: граничные переходыПолучим вторую космическую скорость, характерную для нашей вселенной. Сохраняя предыдущие3 начальные рассуждения, обозначения и терминологию, образуем новое энергетическое пороговое соотношение
![]() (24)
(24)
Справа в выражении (24) записана потенциальная энергия материального объекта у поверхности нашей вселенной. Таким образом, преодоление этой энергии приводит к смене основного состояния объекта. Объект больше не принадлежит, по крайней мере нашему, макромиру. Трансформируясь, он покидает этот мир. Соответствующая скорость следует из (24):
![]()
Соответствующая этой скорости кинетическая энергия выхода объекта за границу нашей вселенной (по крайней мере — нашего макромира) равна:
![]()
и представляет собой одновременно полную энергию покоящегося объекта. Если при скорости ![]() объект теряет инертную массу, то скорость
объект теряет инертную массу, то скорость ![]() приводит к потере тяжелой массы. В одном из вариантов трансформации объекта происходит его превращение в лучевую форму энергии в соответствии с известным уравнением:
приводит к потере тяжелой массы. В одном из вариантов трансформации объекта происходит его превращение в лучевую форму энергии в соответствии с известным уравнением:
mc2 = hn .
В другом варианте события разворачиваются по сценарию черной дыры. Запишем новое соотношение на основе уже известного выражения3
![]() (25)
(25)
Отсюда следует критический радиус
![]() где Rг – радиус Шварцшильда.
где Rг – радиус Шварцшильда.
Критический радиус R* характеризует выход тела за пределы нашей вселенной, его уход за горизонт событий, как принято сейчас говорить. Это и есть начало образования сингулярности в принятой терминологии. В этом случае, учитывая все физические условия такой трансформации, можно предположить, что объект будет принадлежать к микромиру. В общем случае энергетические пороговые соотношения типа (24), (25) с произвольной левой частью и знаком неравенства “меньше, равно” или “больше, равно” должны характеризовать различные случаи входа и выхода некоторого объекта через границу нашей вселенной соответственно.
В удивительном свете предстает перед нами ряд Слов и событий из Священного Писания. Новое и неожиданное толкование приобретают эти Слова и события в контексте с обсуждаемым нами законом:
преображение, воскресение и вознесение Спасителя;
“Сеется тело душевное, восстает тело духовное. Есть тело душевное, есть тело и духовное.” (IКор.15:44).
“ ... не все мы умрем, но все изменимся
Вдруг, во мгновение ока...” (IКор.15:51,52).
“... времени уже не будет.” (Отк.10:6).
3.2. Болезни векаВвиду того что обсуждаемый нами закон носит фундаментальный характер, представляются весьма актуальными в его рамках поиск соответствующих энергетических пороговых соотношений, разработка ранней диагностики и профилактики ряда заболеваний. К их числу прежде всего относятся такие системные болезни, как рак и инфаркт. В каждом конкретном случае на этом пути нам предстоит выделить объект, управляющее воздействие на этот объект, основное состояние объекта, возмущение этого состояния. Наконец, нам предстоит определить характерные для основного состояния и возмущения этого состояния энергии. И все это исследование должно происходить в контексте с рассматриваемым заболеванием. Последнее обстоятельство требует, чтобы мы прежде всего нашли адекватный болезни уровень и язык описания объекта.
Рак. Когда и почему делится клетка? Каково основное состояние клетки, предшествующее этому делению? Какой вид возмущения этого состояния приводит к ее делению? Правильные ответы подведут нас к искомому энергетическому пороговому соотношению: мы с открытыми глазами сможем взглянуть на адекватные болезни параметры организма и клетки, в частности будут обнаружены корни лечения, профилактики и ранней диагностики. Постановка задачи в рамках закона сохранения и превращения энергии определенного вида может и должна стать центральной в литературе, посвященной биологии рака. Основная проблема науки — противоречие между системным характером болезни и узкоспециализированными подходами к ней. В нетривиальном случае** болезнь вызвана стоком избыточной относительно нормального основного состояния клетки энергии в последнюю.
В своих предварительных модельных исследованиях мы будем исходить из данных, приведенных в монографии американского цитолога Е. Каудри [15], а также последних достижений генетики в области канцерогенеза. Судя по N-образной кривой зависимости частоты митозов от собственного времени событий, минимальное количество особых точек и соответственно фаз эволюции равно трем. В дальнейшем мы будем рассматривать физический уровень описания клетки. Во-первых, физический язык описания адекватен клетке как макрообъекту. Во-вторых, для нас это наиболее понятный язык, на котором мы хотим продемонстрировать применение обсуждаемого закона.
Первая особая точка на шкале событий может быть связана с началом нормальных деления клетки. Интересно, что такие деления могут представлять собой результат механического воздействия на ядро. Насколько можно судить из экспериментальных данных, клетка обладает достаточно большой вязкостью. Наличие у цитоплазмы такой вязкости позволяет предохранить ядро от несанкционированных кратковременных воздействий. В то же время длительные, но также нецелесообразные воздействия могут быть устранены при наличии у клетки упругих свойств. В частности, не вызывает сомнения, что клетка как макрообъект обладает отчетливой реакцией на сжатие или растяжение. В этом случае до определенного предела соответствующие воздействия будут погашены возникающими упругими силами. Далее события разворачиваются по сценарию звуковой волны (§ 2.2), где собственная энергия возмущения клетки может быть записана в отличном от приведенного виде. В другом варианте события могут развиваться в направлении, аналогичном образованию геофизической или электрической трещины (п.2.2, 2.8). В этом случае результат можно было бы назвать биологической трещиной.
Вторая особая точка может представлять собой начало возникновения аномальных клеток. Такие клетки должны в первую очередь содержать деформированные уродливые ядра. К патогенезу клетки может приводить переход звуковой мягкой волны, переносящей только возмущение, в ударную волну, переносящую вещество. Точнее, речь могла бы идти о первой фазе образования такой волны, связанной с уплотнением цитоплазмы (п. 2.12). В результате должно происходить травмирование ядра. Уменьшение числа делений клеток на этом этапе можно связать с реакцией имунного механизма на клетки-мутанты.
Третья особая точка могла бы характеризовать возникновение собственно раковых клеток. Последние возникают как результат приспособления клетки к массированному энергетическому воздействию в виде жесткой ударной волны за счет изменения текста ДНК. Возникающие клетки представляют собой диких предков цивилизации клеток организма. В норме они являются как бы спящей (связанной) основой нормальных клеток. По этой причине, по-видимому, они выигрывают сражение за жизнь. В частности, безмолвствуют защитные силы организма.
Продвижение к природе рака, направленное на выявление ракового энергетического порогового соотношения, позволит нам подойти к осознанному анализу клеточного уровня (диагностика) и разумно минимальному адекватному воздействию на него (профилактика и лечение).
Инфаркт. Болезнь и ее окончание, в частности, может протекать по сценарию биологической трещины, аналогичной геофизической (§ 2.3) и электрической (§ 2.9) трещинам. Ранняя диагностика в этом случае связана с численным определением энергетического порогового соотношения, записанного для сердца: профилактика и лечение с направленным воздействием на это соотношение таким образом, чтобы уменьшить отношение упругой энергии к гравитационной.
ЗаключениеКогда-то древний народ Израиля вышел из тьмы египетского рабства. В этом великом исходе и последующем открытии земли обетованной людей спасало Слово Божие. Сегодня мы прикоснулись к тайне качественных изменений и начинаем выходить из пелены непонятого. Но освобождение еще впереди. У нас есть Слово, чтобы в третьем тысячелетии войти с Ним в новую землю.
Это Слово было услышано мною как закон сохранения и превращения энергии определенного вида — необходимая часть общего закона сохранения и превращения энергии. Его сущность можно изложить следующим образом.
В физическом объекте под управляющим силовым воздействием стороннего источника возникает возмущение основного состояния. Основное состояние характеризует единство объекта и среды, к которой объект принадлежит. В процессе управляющего воздействия энергия такого возмущения — энергия определенного вида — накапливается или уменьшается в объекте и переходит в энергию нового вида.
Сохранение или превращение энергии определенного вида в физическом объекте зависит от порогового соотношения между собственной энергией возмущения, определенной для объекта, свободного от соответствующей связи со средой, и энергией, характерной для основного состояния.
Объект сохраняет свое основное состояние и, как следствие, энергию определенного вида, если собственная энергия возмущения лежит в границах, определенных для данного основного состояния. В этом случае мы говорим об эволюции объекта: сколь угодно малое управляющее воздействие приводит к сколь угодно малому возмущению основного состояния объекта, сколь угодно малому изменению его текущего состояния.
В противном случае, когда энергетическое пороговое соотношение (неравенство) между собственной энергией возмущения и энергией основного состояния объекта нарушается (меняет свой знак на противоположный), происходит изменение (обновление или смена) основного состояния объекта. В результате возникает новое возмущение, адекватное новому основному состоянию. Происходит видоизменение энергии: энергия предыдущего вида превращается в энергию либо системообразующей связи объекта, либо нового вида возмущения. Скачок в жизни объекта представляет собой преображение или катастрофу предыдущего образа его существования и сопровождается изменением знака неравенства на противоположный. Для родственных объектов соответствующее энергетическое пороговое соотношение выполняет роль коэффициента подобия (частный случай — числа Фруда, Рейнольдса) и образует шкалу жизненного цикла объекта на соответствующей его основному состоянию фазе эволюции. В финальный момент любой фазы эволюции на этой шкале, когда имеет место предельное равенство правой и левой частей энергетического порогового соотношения, взаимодействие между объектом и средой прекращается.
Закон сохранения и превращения энергии определенного вида был помещен мною в самую сердцевину целого ряда разделов физики. И произошло, как мы могли убедиться, взаимное оплодотворение. С одной стороны, идея была апробирована и получила живое наполнение. С другой стороны, ряд весьма важных задач получил полное решение как прямое применение закона. И, наконец, возник целый ряд новых точек зрения на весьма важные проблемы, которые не могут не принести плоды.
Мы живем в особое время, когда наука и Библия сходятся в единой точке зрения на конечность и ограниченность нашего мира. В ОТО конечность и ограниченность нашего мира характеризуют: скорость света, черная дыра и сингулярность внутри черной дыры. Причем скорость света принята предельной для любого материального объекта, черная дыра существует на горизонте событий, а сингулярность представляет область, где сворачиваются пространство и время. Исследования, проведенные в настоящей работе, показывают, что свет и черная дыра являются спутниками нашей вселенной и на этом основании представляют ее окраину. В то же время граница нашего мира, как и выход за его пределы, могут быть определены на шкале энергетического порогового соотношения. Так скорость, с которой объект может покинуть нашу вселенную, примерно в 1,4 раза больше скорости света. Сам объект при этом теряет последний признак нашего мира — тяжелую массу. Энергия такого выхода есть одновременно энергия полного покоя материального тела. Сингулярность есть один из геометрических образов такого выхода. Причем соответствующий особенный радиус коллапсирующего тела есть половина гравитационного радиуса. Законы нашего мира бессильны для такого объекта: пространство и время прекращают свое существование. Ряд болезней, по моему мнению, носит также пограничный характер. К их числу я отношу психические заболевания, рак, СПИД. Эти болезни своими корнями указывают на границу материального и духовного миров. Собственно, само традиционное знание, включающее в себя элементы веры (гипотезы, постулаты) и опыт, так же как и сама вера, на этой границе прекращают свое существование. Можно вспомнить слова Апостола Павла: “Ибо мы отчасти знаем и отчасти пророчествуем; Когда же настанет совершенное, тогда то, что отчасти, прекратится.” (IКор.13:9,10).
Это предопределенное слияние веры и знания указывает на приближение Источника вечной жизни. Чтобы пить из Него, каждый из нас нуждается в духовном очищении, не слепой вере, творческом аналитическом знании.
Мы у порога нового мира4.
Список литературыА.А Богданов. Всеобщая организационная наука. Тектология, изд.3, ч.1-3, М.-Л.,1925-1929г.г.
Ганцевич М.М., Штерн Ю.М. Системный подход к прогнозу резонанса в решетке. //Радиотехника и злектроника. /АН СССР. — 1982. —Т. 27, № 1, С. 34.
Г.А. Соболев, Ю.М. Штерн. Критическое скольжение в модели землетрясения: теория и эксперимент. АН РАН. Физика Земли, №1, 2001г., 85-88.
Ревуженко А.Ф., Стажевский С.Б., Шемякин Е.И. О механизме деформирования сыпучего материала при больших сдвигах // Физ. - тех. проблемы разработки полезных ископаемых. — 1974. — № 3. — С130.
Терцаги К. Механика грунтов в инженерной практике. — М., 1958.
Садовский М.А. О естественной кусковатости пород. // ДАН СССР. — 1979. — Т. 247, № 4. — С. 829.
Фейнман Р., Лейтон Р., Сендс М. Фейнмановские лекции по физике. — Т. 7. — М.: Мир,1977..
Эберт Г. Краткий справочник по физике. — М., 1963
Амитей Н., Галиндо В., Ву Ч. Теория и анализ фазированных антенных решеток. — М.: Мир, 1974.
E.C.Zeeman. A Catastrophe machine. In towards a theoretical biology. C.H.Waddington ed. Edinburg University press, Edinburg. 1968 — 1972. — Vol. 4, pp. 276 — 282.
Митропольский Ю.А. Метод усреднения в нелинейной механике. — Киев: Наукова думка, 1971.
Кухаркин Е.С., Сестрорецкий Б.В. Электрическая прочность волноводных устройств. — М.: Высшая школа, 1963.
Павлов Д.С., Скоробогатов М.А., Штаф Л.Г. //ДАН СССР. — 1983. — Т. 268, № 2.. с. 510.
Алеев Ю.Г. Нектон. — Киев: Наукова думка, 1976.
Каудри Е. Раковые клетки. — М.: Изд-во иностранной литературы. 19
Похожие работы
... фундаментальными, хотя все они в определенной степени способствовали развитию физики в прошлом и настоящем. Было бы полезно систематизировать многочисленные исторические наблюдения и опыты, входящие в курс физики средней школы (и те, которые, по нашему мнению, должны войти в будущем), по их функциональному признаку – реализации определенной задачи и значению в развитии физической науки. Класс ...
... величины являются наблюдаемыми. Напротив, если мы говорим о какой-либо величине и не можем указать способ ее измерения, то она не является наблюдаемой. Такие величины просто не рассматриваются в физике, не являются ее предметом. Далее, физические величины являются достоверными в том смысле, что физический опыт должен обладать свойством повторяемости. Это значит, что при повторении опыт, ...
... пропорциональности V называется коэффициентом Верде [9, с. 373]. Постоянная Верде зависит от свойств вещества, температуры и частоты света [1, с.78]. 2.3 Метод лоренцевой электронной микроскопии При исследовании доменной структуры тонких ферромагнитных пленок, как и в случае массивных ферромагнетиков, могут быть использованы методы порошковых фигур и магнитооптический эффект Керра. Для ...
... . Включение вектор- потенциала электромагнитного поля А в выражение для свободной энергии позволит связать параметр порядка с плотностью сверхпроводящего тока js.7. Электродинамика сверхпроводников. Всякая последовательно развивающаяся наука только потому и растет, что она нужна челове- ческому обществу. ...



0 комментариев